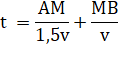|
Édition du: 28/03/2023 |
|
INDEX |
GRAPHES |
||
![]()
|
Le cheval qui sauve le chien Un problème qui permet d'aborder plusieurs
notions:
|
||
|
|
Sommaire de cette page >>> Problème >>> Solution >>> Graphe |
Débutants Glossaire |
|
|
|
|
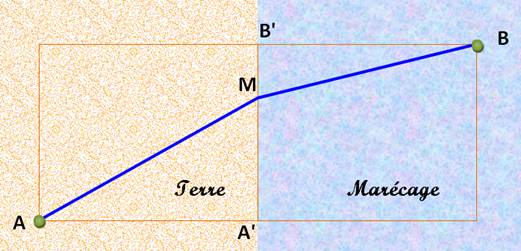
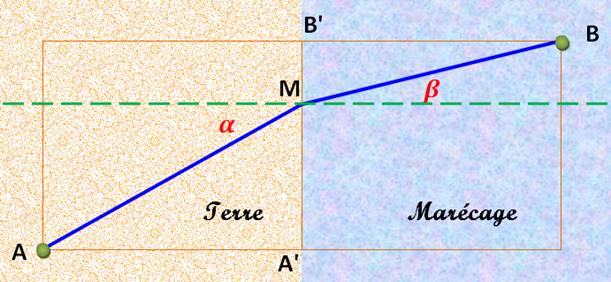
On
donne: AA' = A'B'= BB' = 1 On
pose: A'M = x et v, la vitesse
dans le marécage |
|
|
|
||
|
Temps de
parcours à minimiser |
t = tAM
+ tMB
|
|
|
En multipliant par 1,5 v, une constante. Le problème
revient à minimiser F. |
1,5 v . t = AM + 1,5 MB = F |
|
|
Évaluation des distances |
AM² = 1+ x² MB² = 1 + (1-x)² = 2 – 2x + x² |
|
|
Expression de F |
F = |
|
|
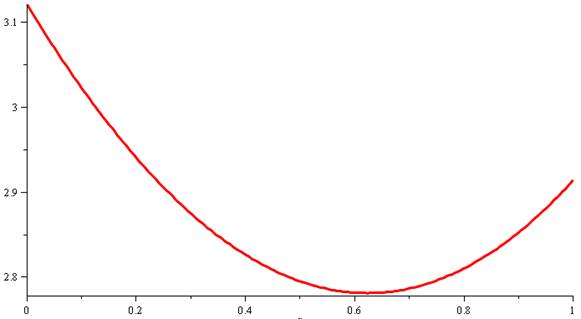
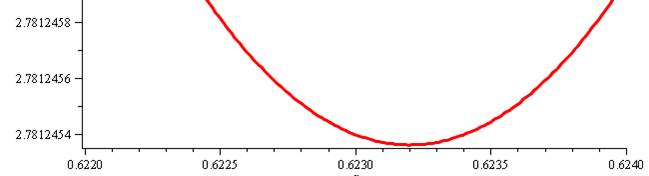
Sa résolution donne la valeur minimale de x |
Fmin = 2, 781245361… pour x = 0,6231997971… |
|
|
|
|
|
|
|
|
|
|||||||
|
Le rapport des sinus
des angles est égal au rapport entre les vitesses. |
|||||||
Bilan
|
Il
est curieux de trouver un problème de ce type qui, en fait, ressemble aux
problèmes d'optique et dont la résolution fait appel aux lois de la réfraction de Descartes
. |
![]()
![]()