géométrie élémentaire: la distance métrique ou ultra-métrique

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 05/01/2023 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	GÉOMÉTRIE
Débutants Géométrie	ÉLÉMENTS de base			Glossaire Géométrie
INDEX Géométrie	Point	Droite	Plan	Parallèle
	Égalité	Distance	Angle	Perpendiculaire
	Sommaire de cette page >>> Distance >>> Devinette – Hauteur de l'arbre >>> Point à point >>> Point et droite >>> Trajet le plus court >>> Médiatrice >>> Cercle et sphère >>> Espace métrique >>> Distance de Hausdorff >>> Distance ultra-métrique >>> Distance intertextuelle >>> Autres distances

Voir Mot DISTANCE dans le DicoMots Maths

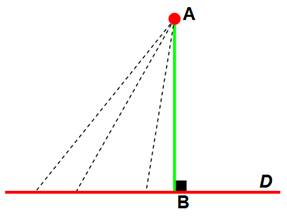
Le directeur de cette entreprise souhaite mesurer la taille d'un poteau. Ses collaborateurs réfléchissent à la méthode:

grimper jusqu'en haut muni d'un décamètre,

mesurer l'ombre portée, ou

faire une visée avec un théodolite.

Pendant ce temps, un ingénieur vint à passer. Mettant ces personnes à contribution, il déloge le poteau, le pose à plat et, avec le décamètre, donne la mesure exacte au centimètre près.

Dépité le directeur s'emporte: impayable ces ingénieurs, après toute ces études, tu leur demandes la hauteur et il te donne la longueur!

Voir Pensées & humour

DISTANCES – Principales notions
*Compas*	On reporte une distance avec un compas. C'est le seul moyen rigoureux.
*Règle*	On mesure les distances avec une règle graduée dont on a, au préalable, convenu d'une unité de mesure.
*Manhattan*	Distance selon un chemin à travers un quadrillage.
*Métrique*	Distance classique.
*Ultra-métrique*	Distance généralisée. Comme la distance entre membres d'une famille.
*Édition* *(Hamming)*	Caractérise la différence entre deux nombres ou deux mots.

Devinette: la hauteur de l'arbre

Problème

C'est un grand chêne. Sa hauteur est connue de la manière suivante: il mesure 9,60 m, plus le tiers de sa hauteur.

Sauriez-vous trouver la hauteur de cet arbre?

Une réponse erronée

L'erreur courante consiste à calculer le tiers de 9,60 = 3,20 et l'ajouter à 9,60 = 12,4 m.

Cette réponse est fausse.

La bonne réponse

Soit L cette hauteur.

Nous savons que L = 9,60 + L/3.

Ce qui donne L – L/3 = 2L/3 = 9,60

On calcule L = 3 x 9,60/2 = 14,4 m

POINT à POINT

Deux points

La plus courte distance entre deux points est la ligne droite.

La distance entre deux points est la mesure du segment de droite joignant ces deux points.

Calcul

*Points*	M₁ (x₁, y₁)
	M₂ (x₂, y₂)
*Distance*	d² = \|x₂ – x₁\|² + \|y₂ – y₁\|²

|x₂ – x₁| = valeur absolue de la différence.

Dis-papa, c'est loin New York? Tais-toi et nage!

Voir Pensées & humour

POINT et DROITE

Un point, une droite

La distance d'un point à une droite est la longueur du plus court segment joignant ce point à un point de la droite.

La droite portant ce segment est perpendiculaire à la droite initiale.

AB est la distance la plus courte.

Tous les autres segments issus de A sont plus longs.

En B, l'angle est droit.

C'est une définition de l'angle droit.

Calcul

*Point*	M₀ (x₀, y₀)
*Droite*	ax + by + z = 0
*Distance*	d = \|ax₀ + by₀ + z\| / (a² + b²)

Voir Bissectrice

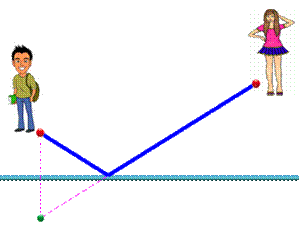
Trajet le plus court entre deux points via une droite

Connu aussi sous le nom de: problème de Roméo et Juliette

Alexis se propose d'amener un livre à Pauline. Il doit cependant s'approcher du tapis roulant pour y déposer son sac à dos. Quel est le chemin le plus court ?

Si Alexis se trouvait de l'autre côté, à la même distance du tapis (position symétrique), il irait tout droit.

Notons le point où il aurait déposé son sac.

Alexis doit alors rejoindre le point de dépôt du sac et se diriger vers Pauline.

Évidemment, on aurait le même chemin en prenant la position symétrique de Pauline.

On trouve d'autres exemples comme la vache ou la chèvre qui va boire à la rivière avant de rentrer à la ferme.

Ou encore: deux villes puisant leur eau courante à la rivière le long de tuyaux rectilignes de la plus courte longueur possible. Où faut-il puiser l'eau ?

Version anglaise: Shortest way to help grandma

You and your grandma live on the same side of the river. You need to find the shortest way to walk from your house to the river (with an empty bucket), fill the bucket with water and bring the water to your grandma. The river is fierce and you cannot swim in it. Disregard the fact that it is much harder to walk with a full bucket than with an empty one. Just look for the shortest path.

Votre grand-mère et vous habitez du même côté de la rivière. Vous devez trouver le plus court chemin pour aller de votre maison à la rivière (avec un seau vide), remplir le seau et apporter l'eau à votre grand-mère. Le courant est fort et vous ne pouvez pas y nager. Négligez le fait qu'il est plus difficile de marcher avec un seau plein que vide. Cherchez simplement le chemin le plus court.

Voir / Brève 915 / Énigmes – Index / Optique / Chemin le plus court pour la fourmi /

Chemin le plus court dans un graphe

MÉDIATRICE

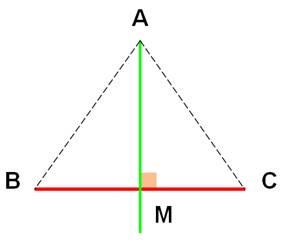
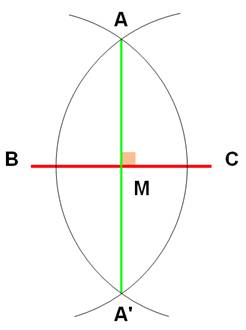
Médiatrice de BC

M milieu de BC.

AM perpendiculaire en M à BC.

Tous les points de la droite portant AM sont à égale distance des points B et C.

Cette droite est la médiatrice du segment AB.

Construction

Soit une ouverture du compas.

De B comme centre, on trace les arcs de cercles en haut et en bas (région de A et A')

De C comme centre, on trace les arcs de cercles en haut et en bas (région de A et A')

Les points de rencontre A et A' définissent la médiatrice

Suite en Médiatrice

CERCLE ET SPHÈRE
*Un point, un plan*	L'ensemble des points à une distance r d'un point O est un cercle: son centre est O et son rayon est r.
*Un point, l'espace*	L'ensemble des points à une distance r d'un point O est une sphère: son centre est O et son rayon est r.

ESPACE MÉTRIQUE – Définition
*Axiomes*	Distance métrique sur un ensemble E: Application d de E² dans R₊ telle que pour *x, y, z* de E:
*de séparation*	d(x, y) = 0	ssi x = y
*de symétrie*	d(x, y) =	d(y, x)
*triangulaire*	d(x, y) £	d(x, z) + d(z, y)

Voir Espaces et Espace métriques

DISTANCE DE HAUSDORFF – Notion

Deux segments: un droit et l'autre courbe.

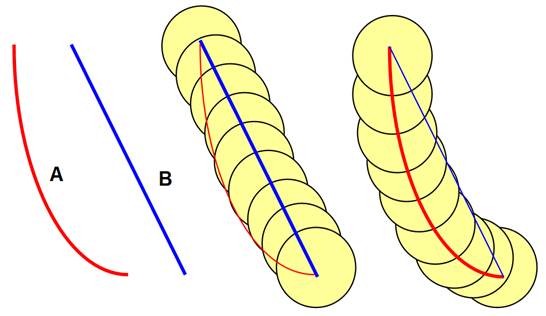
Le rayon r du disque qui permet:

- de couvrir B à partir de la figure construite sur A et,

- de couvrir A à partir de celle construite à partir de B

est la distance de Hausdorff entre A et B.

On peut généraliser à n’importe quels objets.

Défaut: Si on ajoute un point assez éloigné à la courbe A, sa distance à B sera grande alors que les deux figures sont pourtant assez semblables

DISTANCE INFORMELLE – Notion

C’est la longueur du programme le plus court permettant de dessiner la figure B à partir de A.

Distance inventée pour tenter de caractériser des analogies entre objets.

Une maison et la même maison avec du feu à la cheminée sont semblables.

Application au génome.

La distance entre un dessin d’objet et son image inversée est courte: l’œil voit immédiatement que les deux dessins sont semblables.

Défaut: on n’est jamais sûr d’avoir trouvé le programme le plus court.

DISTANCE ULTRA-MÉTRIQUE – Notion

Distance telle que: d (x, y) max { d (x, z) , d (z, y) }

Exemple

Distance dans un graphe, dans un arbre généalogique.

Distances

Les distances ne s’ajoutent pas.

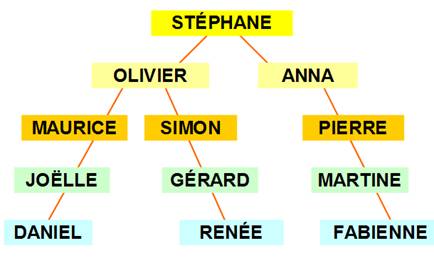
Par contre la propriété suivante peut être vérifiée:

d (x, z) { d (x, y), d (y, z) }

d (Daniel, Fabienne) { d (Daniel, Renée), d (Renée, Fabienne) }

8 { 6, 8 }

Une distance ayant une telle propriété est dite ultra-métrique.

On ne considère pas la somme des distances mais seulement la plus grande des deux.

Avec une distance métrique, on aurait: d (x, z) d (x, y) + d (y, z)

Cette notion de distance est utilisée avec les nombres p-adiques. La distance p-adique caractérise la divisibilité d’un nombre par un nombre premier choisi et par ses puissances.

Théorème de Viviani

Pour tout polygone régulier, la somme des distances d'un point intérieur quelconque aux côtés est égale à la longueur de la hauteur. >>>

Suite	Diagramme de Voronoï Distance à l'horizon Distance de sécurité en voiture Distance entre deux points géographiques Distance intertextuelle Distance ultra - métrique Distances dans l'univers Angles
Voir	Base de la géométrie: la droite Bissectrice Construction au compas Constructions avec des allumettes Diamètre Géométrie – Index Jeux – Index Jeux divers Périmètre Points Polygones Somme des entiers Symétries motifs de frises et tapisseries
Dicomot	Glossaire des termes de mathématique
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/distance.htm