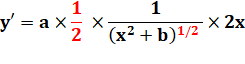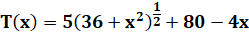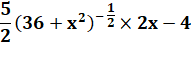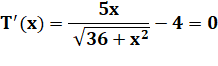|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
DÉRIVÉES – Exemple avec racines Célèbre problème poser à des
étudiants écossais et considéré comme trop difficile; d'ailleurs objet d'une
pétition (presse d'octobre 2015). |
|
|
||
|
Problème |
||
|
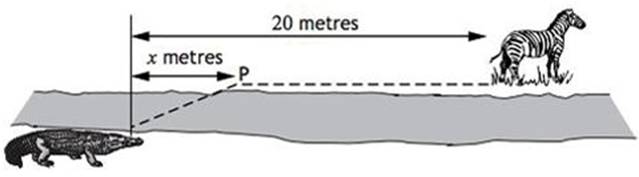
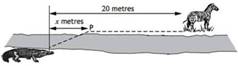
Le zèbre
est à 20 mètres du crocodile, mais de l'autre côté de la rivière. Sachant que
la vitesse du crocodile est différente sur terre et dans l'eau, calculer la
distance x au point P tel que le crocodile minimise son temps pour atteindre
le zèbre. |
Le temps en fonction de x est connu en dixièmes
de secondes par la formule:
|
|
|
Résolution Calcul
des points extrêmes (en fait, demandé dans l'énoncé original). |
|
|
L'optimum
est atteint lorsque la dérivée de T(x) est nulle. |
|
|
Rappel de la dérivée d'une racine - la puissance devient coefficient (1/2); - la nouvelle puissance est égale à l'originale
moins un (soit -1/2); et - la dérivée de l'expression sous la racine est
multiplicative. |
|
|
Notre
expression en introduisant une puissance
fractionnaire: |
|
|
Sa dérivée: |
|
|
Mise en
forme et égalisation à 0 pour trouver l'optimum. |
|
|
Passage
au carré et calculs. |
25x² = 16 (36 + x²)
9x² = 576
x= 8 |
|
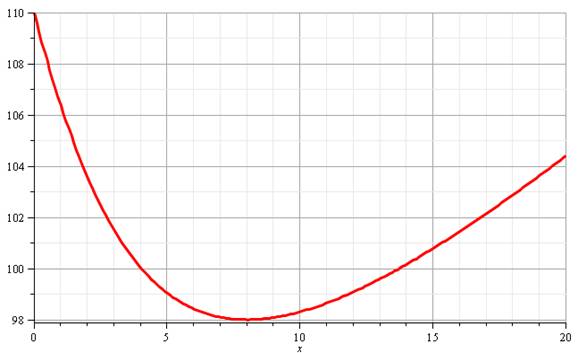
L'optimum
est atteint pour x = 8 et pour 9,8 seconde; un peu moins que dans les deux
cas extrêmes. |
|
|
Vérifications |
|
|
Variation
de la fonction Le point
x = 8 est bien un minimum. |
|
|
Graphe |
|
![]()
Les trois problèmes récents présentés par la Presse de 2015
|
|
|
|
|
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette
page |
http://villemin.gerard.free.fr/aMaths/Analyse/DerivInt/Crocodil.htm
|
![]()