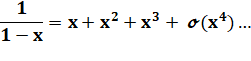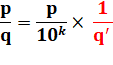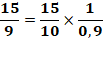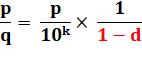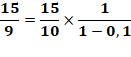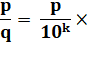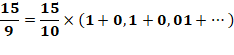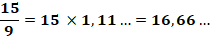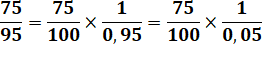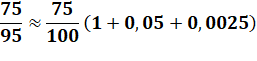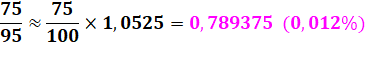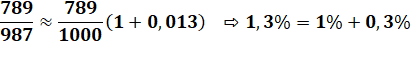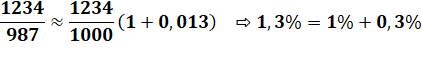|
|||||||||||||||||||||||||||||||||
![]()
|
Division rapide par additions Application des développements
limités Un
exemple de calcul
rapide appliqué à la division
qui permet d'estimer rapidement un ordre de grandeur (presque) de tête. La
qualité du résultat est d'autant plus grande que le diviseur est proche d'une
puissance de 10. D'autres
calculs (racine carrée, exponentielle …) sont
faisables de la même manière. |
|
|
||||
|
Dans le cas où le diviseur est proche d'une puissance de 10, il est
possible de calculer rapidement un ordre de grandeur du quotient en utilisant
ce développement
limité (qui est, dans ce cas, la formule de la série géométrique). Voyons
le principe |
Le petit o
indique que l'erreur est de l'ordre de la puissance quatrième. |
|||
|
On isole une fraction avec dénominateur inférieur à 1. |
|
|
||
|
Le dénominateur est mis sous la forme du complément à 1. |
|
|
||
|
La fraction de droite peut être exprimée par un développement limité
(d étant petit). |
|
|
||
|
|
||
|
Calculez |
75 / 95 = 0,7894738… |
|
|
Calcul complet du second ordre Mettre la fraction sous la forme du
développement. On a pris 5, le complément de 95 à 100. |
|
|
|
Calcul mental du premier ordre On profite du 5 pour multiplier par 10 et diviser
par 2. |
75 + 5% = 75 + 7,5 / 2 = 75 + 3, 75 = 78,75 Résultat: 0,7875 (0,25 %) |
|
|
Calcul mental du second ordre Un peu moins facile en calcul mental. On peut simplement dire: j'ajoute une toute
petite "pincée": 0,7875 => 0,789. |
78, 75 + 25pour 10 000 de 75 (ou 25% de 0,75) 78, 75 + 0,2 (approximation) 78, 95 Résultat: 0,7895
(0,003%) |
|
|
|
||
|
Calculez |
789 / 987 = 0,7993920973… |
|
|
Calcul mental du premier ordre |
789 + 7,9 + 2,4 = 799,3 Résultat: 0,7993 (0,01%) |
|
|
Calculez |
1234 / 987 = 1,250253293… |
|
|
Calcul mental du premier ordre |
1234 + 12,34 + 3,7 = 1250,04 Résultat: 1,25004 (0,017%) |
|
|
Appréciation
de la pertinence |
|
|
|
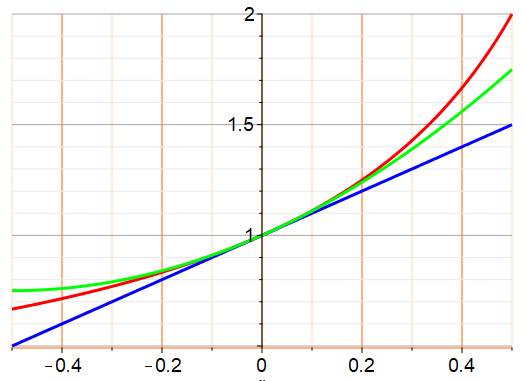
Graphes On cherche à apprécier la
qualité de l'approximation.
Erreur vite importante avec le
premier ordre; même avec le second ordre, ne pas dépasser x = 0,2 |
|
|
|
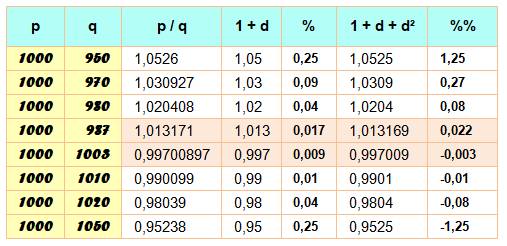
Exemples de calculs (exacts) avec les formules d'approximations
du premier (erreur en %) et du second ordre (erreur en pour 10000). |
|
|
Merci
à Anthony Canu pour l'idée de cette page
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Analyse/Develop/Division.htm
|
![]()