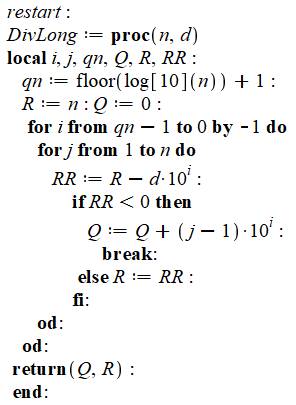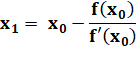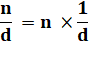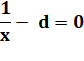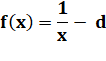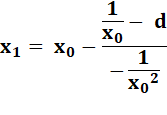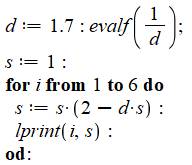|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Algorithmes de DIVISION But: revue des algorithmes de calcul de la
division sans réaliser la division. Applications: Méthodes utilisées pour la mécanisation de la
division sur ordinateurs, en dur
(en hardware). Alors que l'addition et la multiplication ont fait l'objet de
soins attentifs pour accélérer les calculs, la division avait pris du retard.
Elle est devenue de plus en plus demandée pour la réalisation des unités de
calcul flottant*: calcul d'images dans les cartes graphiques, par exemple. * UVF: unité
de calcul en virgule
flottante ou FPU: Floating-point unit |
Anglais: Computer arithmetic, decimal floating point units,
a
radix-10 digit-recurrence division unit
|
|
||
|
1) Récurrence
sur les chiffres |
Calcul
du quotient chiffre par chiffre à la
manière de notre division
posée. Ces algorithmes produisent le quotient et le reste. Opération: une soustraction par itération. Convergence linéaire Le temps de calcul est directement fonction de la
longueur des dividendes et diviseurs. Méthode couramment utilisée: SRT, du nom de ses
inventeurs indépendants : Sweeney, Robinson, and Tocher. |
|
|
2) Itération
fonctionnelle |
Utilisation
de fonctions d'approximation que l'on fait converger vers le quotient. Le
reste n'est pas disponible Opérations:
deux multiplications par itérations. Convergence
quadratique (beaucoup plus rapide que linéaire) Méthode
Newton-Raphson. |
|
|
3) Récurrence
sur plusieurs bits (high radix division) |
Méthode
identique à la première, mais traitant des blocs de plusieurs bits (8, 10,
16). Opération:
multiplications Complexité:
supérieur à 1), mais inférieure à 2). Convergence:
linéaire (plus de temps que 2) ). |
|
|
4) Latence
variable |
Le
temps de calcul (de latence) est adapté selon la taille des dividendes et
diviseurs. Convergence
plus rapide que les trois autres. Complexité:
nécessite un système de gestion de la latence. |
|
|
Note: chacune
de ces méthodes se sont retrouvées
implémentées en matériel (hardware), soit sur des cartes électroniques (dans
le passé) ou sur des circuits intégrés. Anecdote: j'ai eu
à concevoir ce genre de cartes électroniques autour des années 1970 pour
réaliser un calculateur dit "avaleurs de données" (number
crunchers) sur 24 bits. Les microprocesseurs n'étaient pas encore nés. |
![]()
|
Note: les
programmes proposés sur cette page à titre de
découverte fonctionnent dans les cas ordinaires. Les cas pathologiques
ne sont pas pris en compte (division par 0, division de nombres négatifs …) |
|
|
||
|
Contexte Méthode
la plus simple et la plus ancienne, figurant dans Les Éléments d'Euclide. |
Algorithme N est le nombre à diviser par D, Compter combien de fois on peut soustraire D de N et retenir cette
quantité. |
|
|
Maple
|
Python
|
|
Voir Division
par récursivité / Programmation
– Index
|
|
|||
|
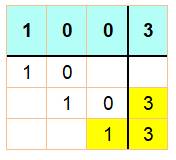
Contexte Méthode qui utilise la
méthode de la division
posée (classique). Division posée (ou longue)
100 = 3 x 33 + 1 Un chiffre du quotient est déterminé par: combien
de fois le diviseur pour approcher la partie du dividende en cours d'analyse. Exemple: combien
de fois 3 pour approcher 10. Réponse 3 car 3 x 3 = 9, mais 4 x 3 = 12, c'est
trop. |
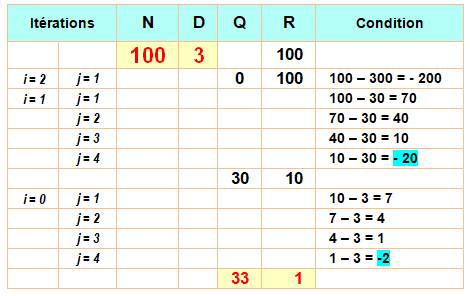
Formule de la division R initial = N; i est le numéro du chiffre de N.
Un nouveau reste est égal au précédent auquel on
retranche une quantité suffisante (qi) de fois le diviseur (D). Itérations: autant de fois qu'il y a de chiffres dans le dividende (N). Les chiffres qi du quotient sont
déterminés par essais de soustractions successives: autant que nécessaire
pour faire basculer la différence en négatif. Tableau valant algorithme N: dividende; D: diviseur; Q: quotient; et R = reste
|
||
|
Programme : procédure
Programme principal
|
Commentaire Programme qui suit le tableau ci-dessus. Réinitialisation générale. Définition de la procédure de division longue
avec déclarations des variables utilisées dans la procédure. La longueur
du dividende qn est calculée par cette formule en logarithme à base 10. La variable R (le reste) prend la valeur N, et
sera décrémentée au fur et à mesure des calculs. Le quotient Q est initialisé à 0. Boucle de recherche des chiffres du quotient,
l'un après l'autre, en commençant par le chiffre le plus à gauche (de poids
10qn). La variable q est le compteur de soustractions;
combien de fois retire-t-on le diviseur dans le dividende avant d'obtenir une
différence négative. Cette quantité sert à calculer le quotient Q. Dès que
cette valeur est trouvée, arrêt de la boucle (break). Sinon, on continue en prenant le nouveau reste (R
= RR). Arrêt, lorsque tous les chiffres (qn) du
dividende ont été analysés. Exemple de traitement avec toutes les divisions
de 100 par 5 à 10. Exemple: 100 / 6 = 16 et reste 4. |
||
|
Division longue binaire |
|
|
|
Contexte Méthode
qui utilise la méthode de la division
posée (classique) mais exécutée en binaire
(propice à la logique d'un ordinateur) Les
opérations binaires à réaliser sont alors soit des décalages soit des
opérations logiques (ET).
Opérations simples à réaliser par des circuits
logiques. La
programmation est réalisable mais ne reflète pas la simplicité de ces
algorithmes sur du binaire. D'autres types de divisions binaires sont
proposés sur la page Wikipédia en anglais |
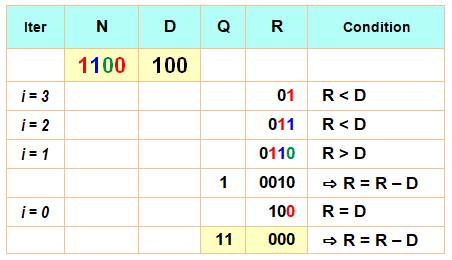
Algorithme (les nombres sont exprimés en binaire) N = 1100; D = 100; Q = 0; R = 0 Pour i de 3 à 0 R = R auquel on ajoute le
bit N[ i ] en position R[ 0 ] Si R est supérieur ou égal
à D alors Q[ i ] = 1 Fin du Si Fin du Pour Algorithme sous forme de tableau
|
|
|
|
||||
|
La méthode de
Newton est utilisée pour approximer les racines d'une fonction. Si x0
est une racine proche x1 sera encore plus proche |
|
|||
|
Pour
effectuer une division on multiplie par l'inverse du diviseur. Le but
est de calculer l'inverse du diviseur. On le multiplie par n en fin de
calcul. |
|
|||
|
Le
diviseur est la racine de la fonction f(x) |
|
|||
|
Application
de la méthode de Newton Voir
Dérivées
usuelles |
|
|||
|
Exemple Calculer l'inverse de 1,7. Avec une semence s = 1, en six itérations, la méthode produit huit
chiffres significatifs. |
|
|
||
|
Une petite idée de la réalisation Pour passer à la
réalisation, nous allons utiliser un artifice très courant en maths: changer
de monde, y travailler et revenir au monde originel. |
On va calculer la valeur de d dans l'intervalle
0,5 à 1. On dit que l'on normalise. On effectue les calculs dans cet intervalle et on
re-déploie (on dé-normalise) en fin de traitement. Exemple avec x0 =
3 = 11 en binaire. En divisant par 2 , on a: 1,1 (décalage d'un
cran). Encore par 2, on a: 0,11 qui est un nombre un peu
plus grand que 0,5 mais inférieur à 1. Cette opération de division par 22
(décalage de deux crans vers la droite) cadre le nombre entre 0, 5 et 1. |
|
|
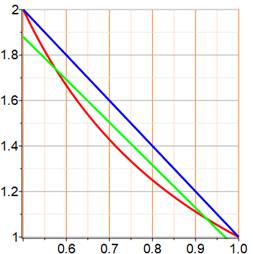
Approximation dans l'intervalle Que
devient notre approximation dans cet intervalle?
Implémentation Hors du cadre de ce site. Voir les références in
fine. |
|
|
|
Cette page décrit succinctement comment les scientifiques
développent des algorithmes pour implanter la division dans les circuits. Il
s'agit d'user d'ingéniosité pour minimiser le compromis vitesse de calcul et
complexité de la réalisation. La description plus détaillée est une affaire de
spécialistes. Se reporter aux nombreux textes (pointus)
qui sont disponibles sur le Web. |
![]()
|
Voir suite en |
|
|
Voir |
|
|
Sites |
|
|
Sites pour experts |
|
|
Cette page |