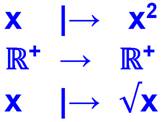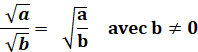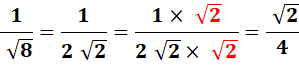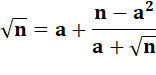|
||||||||||||||||||||||||||||||||||||
![]()
|
RACINE CARRÉE
|
Voir Fonctions réciproques
|
C'est
l'histoire d'un neuf qui se
promenait. Il traverse une forêt. Il
en ressort transformé en trois! Que
s'est-il passé? Nul
doute, il est tombé sur une racine! |
|
Stromae sort un album
intitulé racine carrée en août 2013. Il
indique que racine renvoie aux origines numériques et carrées, car il aime
les formes géométriques. Il ajoute:
je fais de la musique comme si je faisais des maths. Stromae
(né en 1985) est le verlan de Maestro. Son
vrai nom est Paul Van Haver. |
Voir Pensées & humour
|
SOMMET EUROPÉEN des 22 et 23 juin 2007: où
il est question de racine carrée Le (mini-) Tr
À superficie voisine, la population allemande est plus que
deux fois celle de la Pologne. En utilisant la racine carrée de la population le
différentiel redescendrait à environ 1,5. |
Voir Europe / Pensées
& humour
Petit
calcul amusant: résoudre l'équation
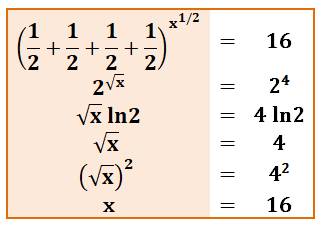
![]()
|
|
||
|
Puissances
et racines >>> Carrés
(Nombres - ) >>> Puissances et
racines – Index >>> Racines nièmes >>>
Racine d'une équation Racines
carrées – Définition et propriétés >>> Racine carrée –
Introduction et notations >>>
Racine carrées – Glossaire >>>
Racine carrées – DicoMots Maths >>> Racines carrée
continues Racines
carrées – Valeurs >>> Table de racines carrées
de 1 à 10 >>>
Table des racines de 1 à 10 jusqu'à 100 >>> Racine
de -1 (Imaginaire) >>> Racine de 2 >>>
Racine de 2 – Spectre >>>
Racine de 2 – DicoNombre >>> Racine de
2 – En géométrie >>>
Racine de 2 et de 62 - Motifs >>> Racine de 3 >>> Racine de 5 >>> Racine de 8 Autres
racines >>>
Racine cubique: calcul à la main >>> Racine 13e
– Calcul mental >>>
Racines de l'unité (complexes) |
Calcul
de la racine carrée >>> Babylone
(Algorithme de - ) >>>
Brahmagupta (Approximation de -) >>>
Calcul à la main (comme la division à la française) >>>
Calcul à la main (explications géométriques) >>>
Calcul à la main (explications, fondements) >>> Calcul avec Maple Opérations
avec les radicaux >>> Calcul avec radicaux
– Nombreux exemples >>>
Calcul avec radicaux – Formulaire >>>
Calcul mental >>> Calculs
- Index >>>
Carrés parfaits (Racine mentale des -) >>>
Construction géométrique >>>
Cubique (Fonction d'approximation) >>>
Décimales des racines carrées >>>
Développements limités >>>
Dichotomie (Méthode par - ) >>>
Écarts (Méthode des -) >>> Fraction
avec dénominateur sans radical >>>
Fractions continues et calcul des racines >>>
Goutte à goutte (Méthode du -) >>> Héron
(Méthode de - ) – Algorithme de Babylone >>>
Impairs (Méthode du goutte à goutte) >>>
Newton (Méthode de - ) >>>
Racine des nombres en 9999… >>>
Racines consécutives – Énigme >>>
Sommes de racines presque entières |
|
![]()
|
|
|||||
|
Not |
2
Notation fractionnaire Notation sans exposant |
||||
|
Définition |
La racine carrée d’un
nombre a est un nombre dont le carré vaut a: |
r = r² = |
|||
|
À retenir!!! |
Un nombre est égal au
produit de sa racine par sa
racine. J'ai un doute, je me conforte
en prenant un exemple numérique. |
en effet: 3
. 3 = 9 |
|||
|
M |
L’application: est une bijection de: dont la réciproque est
notée: |
|
|||
|
Existence |
Tout nombre réel possède deux racines opposées: -
l'une positive: la racine ou racine principale; -
l'autre négative et de même valeur. |
Exemple
Car 2 x 2 = 4
Car (–2)( –2) = 4 |
Général
Notation |
||
|
Deux racines ou une? |
Racines
carrées de 25 = |
-
5 et + 5 |
|||
|
Par contre, le radical,
indique que l'on s'intéresse à la racine carrée principale, celle positive |
|
=
5 |
|||
|
Cette distinction est subtile
et rarement respectée. Elle est présente chez les Anglo-saxons |
|
||||
|
Le
logiciel Maple propose deux
façons de calculer la racine carrée:
Voir Calcul
des racines énièmes avec root et surd – Pièges! |
Voir Racine
carrée et notation symbolique de i (imaginaire)
selon que l'on admet la racine négative d'un nombre ou
non.
Table des racines de n et
de 1/n aux puissances 1 à 5
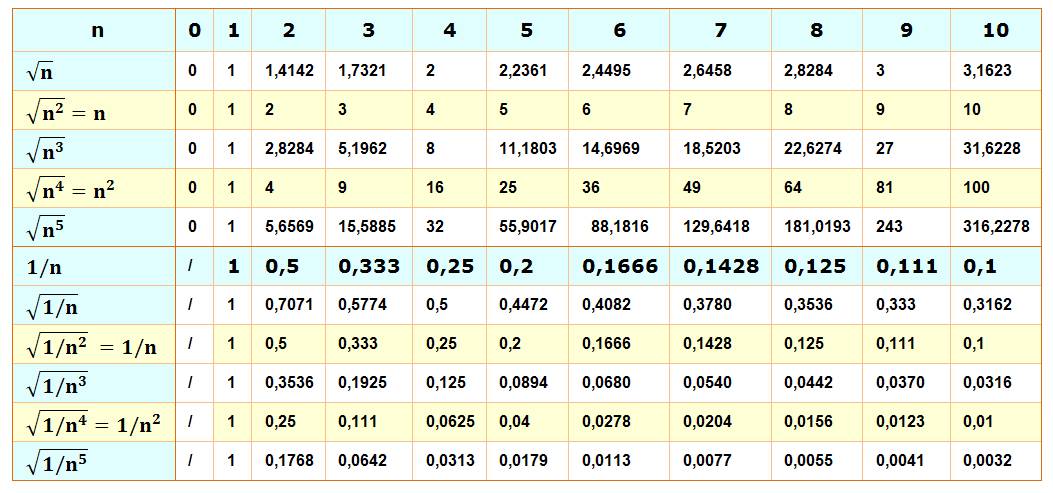
Exemple de
lecture: la
racine carrée de 3 est 1,7321 et celle de 1/3 est 0,5774.
Notez que la racine carrée du carré de n est
égale au nombre n. Normal!
Voir Tables
|
|
|||
Voir
Toutes
les formules Sous le radical
Piège!
|
|||
SUITE en page spéciale: calculs avec radicaux
Une identité utile au calcul de fractions continues
|
|
Démo et application >>>
|
|
||
|
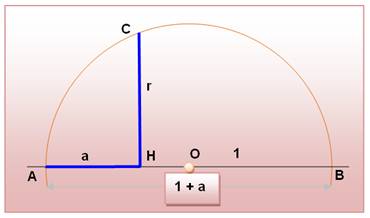
r² = OC² - HO²
4r² = (1 + a )² – (1 – a)² = 1 + 2a + a² – 1 + 2a – a² = 4a r = Exemple: (ne soyez
pas surpris que r soit plus grand que a)
|
OC est le rayon = (1 + a) / 2 OH = OA – a = (1 + a) / 2 – a = (1 – a ) / 2 |
|
Voir Autre
construction
|
|
||
|
|
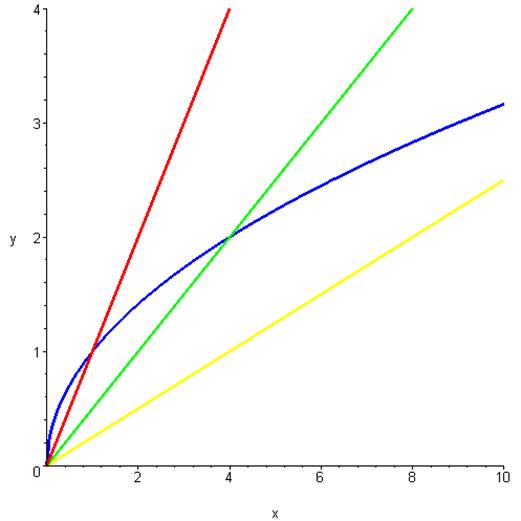
Rouge y = x Verte y = ½ x Bleue y = 2 J Notez x = 2 pour x = 1 ½ x = 2 pour x = 4 ¼ x = 2 pour x = 16 (hors
figure) |
|
|
|
|
|
a =
2 = 1,
414213562373095048801688724209698078569671875376948073176679737990732478462107038850387534327641573
3 =
1,
732050807568877293527446341505872366942805253810380628055806979451933016908800037081146186757248576 4 =
2 5 =
2,
236067977499789696409173668731276235440618359611525724270897245410520925637804899414414408378782275 6 =
2,
449489742783178098197284074705891391965947480656670128432692567250960377457315026539859433104640235 7 =
2,
645751311064590590501615753639260425710259183082450180368334459201068823230283627760392886474543611 8 =
2,
828427124746190097603377448419396157139343750753896146353359475981464956924214077700775068655283145 9 =
3 10 =
3,
162277660168379331998893544432718533719555139325216826857504852792594438639238221344248108379300295 11 =
3,
316624790355399849114932736670686683927088545589353597058682146116484642609043846708843399128290651 12 = 3, 464101615137754587054892683011744733885610507620761256111613958903866033817600074162292373514497151 |
|
|
APPLICATIONS |
|||
|
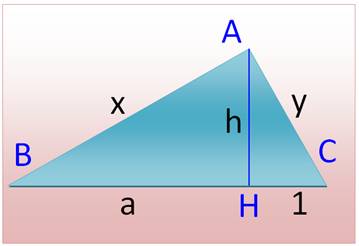
Géométrie |
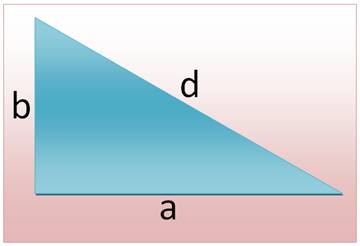
Théorème de Pythagore: d = - hypoténuse du triangle
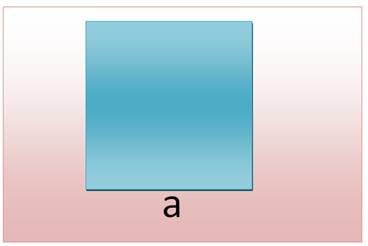
rectangle, ou - diagonale du rectangle. Côté du carré
connaissant son aire: a = Construction de (règle et comp x² + y² = (1 + x² = y² = 1² + h² 2h² = 2ª h² = h = |
Tracer
BH et prolonger d'une unité en C. Dessiner
le cercle de diamètre BC (via la médiatrice). Perpendiculaire
en H coupe le cercle en A. |
|
Voir Constructions
géométriques élémentaires
|
Publicité |
|
|
|
|
|
ENGLISH CORNER |
||||||
|
Words |
|
|||||
|
Definition |
A squ Square: the result of
multiplying the number by itself. |
|||||
|
Theorem |
Square roots of integers that
are not perfect squares are always irrational numbers. |
|||||
|
Abbrevi |
Sqrt(x) |
|||||
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()