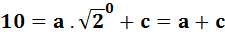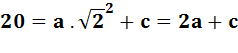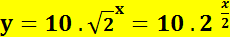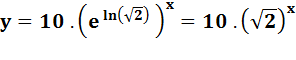NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 16/10/2016 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Puissances
Débutants Exponentielle	Croissances			Glossaire Général
INDEX Puissance Décomposition	Exponentielle	Cinq ans	Calcul fonction
	Terminale	Sommaire de cette page >>> Recherche d'une fonction >>> Utilisation du tableur >>> Changement de base exponentielle

EXPONENTIELLE

Calcul des paramètres de la fonction

Exemple de calcul.

Recherche d'une fonction
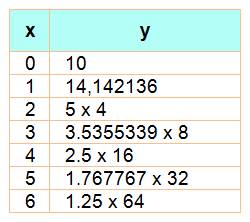
On donne ce tableau mystérieux. Trouver l'expression fonctionnelle: y = f(x)
Dans ce tableau, je remarque la racine de 2.	1, 41 42 = 14, 142136 = 10 x
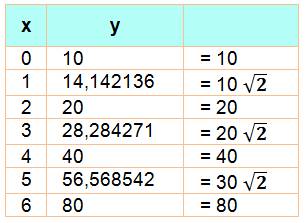
Idée de l'allure de la fonction Ce qui donne ce nouveau tableau en faisant les calculs. Les valeurs10, 20, 40, 80, qui doublent, font penser à une progression exponentielle. Effectivement je passe d'un nombre au suivant en multipliant par racine de 2.
Mise en équation Le facteur multiplicatif est racine de 2.
L'équation de la courbe est du type:
Utilisation de deux couples; Calcul de la différence; Puis calcul des coefficients.
La fonction est finalement:

Utilisation du tableur
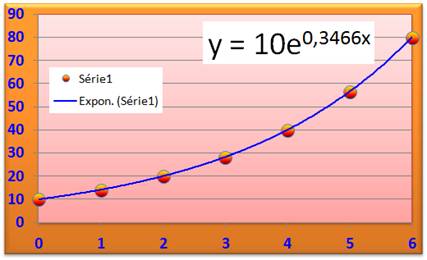
Attention n°1 Il est intéressant de se donner une idée de la courbe et de son équation en utilisant un tableur. En demandant la courbe de tendance et son équation, Excel donne une curieuse formule qui n'est pas celle que nous avons trouvée. Alors?	La courbe de tendance vous est proposée en cliquant directement sur les plots affichés.
Réconciliation Cette formulation s'écrit aussi:
Petit calcul sur les puissances:
Attention n°2 Bien choisir le type d'insertion de courbes sur le tableur.	Ne pas prendre ligne qui risque de créer des problèmes de décalge des abscisses, mais plus sûrement le nuage de points.

Changement de base exponentielle

Nous venons de retrouver la formule de changement de base en exponentielle:

En effet nous avons:

Voir Changement de base en logarithme

Suite	Exponentielle Logarithme
Voir	Croissance du nénuphar Enseignement – Index Pourcentages Table – Index
DicoNombre	Racine de 2
Site	La recherche de la règle d'une fonction exponentielle – Allo prof Exponentielle de base a – Wikipédia
Cette page	http://villemin.gerard.free.fr/aMaths/Analyse/Puissanc/CalExpon.htm