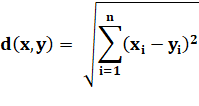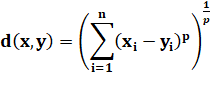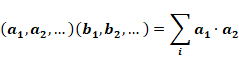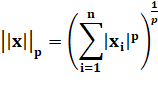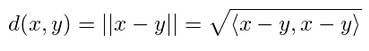|
Édition du: 01/12/2022 |
|
INDEX |
Théories modernes |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Espace de Hilbert – Notion Comment
introduire les espaces de Hilbert ? Nous allons reprendre quelques notions de
base, pas à pas, pour introduire ces espaces. L'espace classique
ne s'accommode pas bien de l'infini.
Les espaces de Hilbert ont été inventés par David
Hilbert (1862-1943) pour résoudre des problèmes de cet ordre. Ce sont
d'ailleurs les espaces de dimension infinie
les plus simples. Applications aux transformées
de Fourier, aux équations
différentielles et, plus particulièrement, à la mécanique
quantique. Les
espaces de Hilbert font partie de l'analyse fonctionnelle en mathématiques. Le
concept d'espace de Hilbert étend les méthodes de l'algèbre linéaire en
généralisant les notions d'espace classique à des espaces de dimension
quelconque (finie ou infinie). En bref: un espace de
Hilbert est un espace muni d'une distance particulière définie par un produit
scalaire qui satisfait la complétude: les suites de
nombres y sont toutes convergentes. Il permet de mesurer des longueurs et des
angles et de définir une orthogonalité. |
||
|
|
Sommaire de cette page >>> Qu'est-ce qu'un espace ? >>> Espace topologique >>> Espace métrique >>> Suite de Cauchy et complétude >>> Espace vectoriel normé >>> Espace préhilbertien (inner product space) >>> Espace de Hilbert >>> Un des propriétés des espaces de Hilbert >>> Lecture – Historique |
Débutants Glossaire |
Anglais: Hilbert space: an inner product space which satisfies completeness
Ceci n'est pas un espace
de Hilbert
|
Tentons un
contre-exemple pour approcher les espaces de Hilbert. Prenons une
marche d'escalier et sa rampe. La rampe peut être plus ou moins pentue, mais
jamais verticale. Partant d'une certaine inclinaison, on peut la rendre plus
raide en augmentant la pente à chaque pas de la moitié de l'angle qui reste
pour atteindre la verticale, par exemple. Avec beaucoup d'itérations,
on se rapproche de plus en plus d'une rampe verticale. Mais on n'y arrive
jamais tout à fait (paradoxe d'Achille). Toutes ces
rampes forment une collection de rampes que nous appellerons l'espace des rampes. Cet espace de rampes de
plus en plus raides n'est pas un espace de Hilbert, car l'état final n'est
pas du tout une rampe. |
|
Espace et notre espace ordinaire L'espace dans "Espace de Hilbert", est
une construction mathématique et non l'espace ordinaire, celui que nous
entendons normalement. L'espace en mathématiques signifie une collection
de vecteurs
qui interagissent d'une certaine manière. Il est défini par:
L'espace qui nous entoure est un sous-ensemble de
l'espace généralisé ainsi défini. Il est représenté par des vecteurs en trois
dimensions qui suivent la géométrie euclidienne (la géométrie classique, la
géométrie dans l'espace du lycée, dite euclidienne).
|
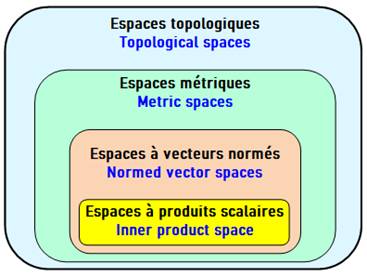
Les divers espaces et leurs
relations L'espace de Hilbert se trouve au plus profond de
cet emboitement des divers types d'espaces.
|
|
|
Les espaces mathématiques En mathématiques, un espace donné est un espace
particulier, muni de structures remarquables, permettant de définir des objets
tels que points, vecteurs, fonctions… Trois exemples ci-contre. |
Un espace topologique
est un ensemble muni d'une structure très générale (la topologie), qui permet
de définir la notion de voisinage d'un point. Cette structure permet de définir
les notions de continuité et de limite. Un espace métrique
est un espace topologique dont la topologie est définie au moyen d'une
distance. Cette dernière permet d'estimer la taille d'un ensemble (diamètre),
la proximité par rapport à un point, etc. Un espace vectoriel
est un ensemble dont les éléments, les vecteurs, peuvent s'additionner et
être multipliés par des scalaires. |
|
Voir Définition
de l'espace dans l'encyclopédie
|
Les espaces sont de deux types:
Note: Il s'agit d'une classification grossière, ils ne sont
pas mutuellement exclusifs. Il existe des espaces métriques qui relèvent des
deux catégories. Les espaces linéaires
sont des espaces vectoriels munis d'opérations linéaires prédéfinies. Les espaces linéaires ont certaines limites. Par exemple,
impossibilité de définir une ligne et un cercle perpendiculaires. Les espaces
topologiques sont plus proches du monde réel et permettent de définir les choses qui nous entourent
comme des surfaces uniformes. En considérant les espaces topologiques, nous
sommes en route vers les espaces de Hilbert. |
Qu'est-ce qu'une topologie ? En mathématiques, la topologie
est définie comme une construction fondamentale de l'espace qui est préservée
suite à une déformation continue comme l'étirement, le pliage, l'effritement
mais pas la déchirure. Le ruban de
Möbius est un exemple populaire de topologie. Objet qui a une seule
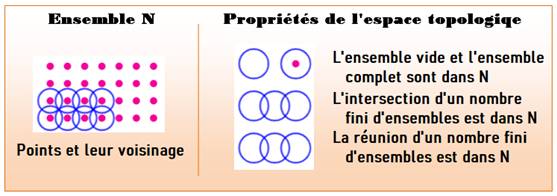
surface et une limite singulière. Définition On définit une topologie sur un ensemble non-vide
X, comme une collection d'ensembles ouverts t dans X, obéissant aux
propriétés ci-dessous:
L'espace topologique est défini comme la paire
(X, t), où t est une topologie sur l'ensemble X. |
|
Ensemble topologique N
|
Métrique Une métrique est une fonction qui calcule la distance
entre deux points dans l'espace. La fonction génère un nombre réel d(x, y) pour
chaque paire La fonction doit satisfaire les propriétés
suivantes:
Ces propriétés sont assez intuitives car elles
sont vraies pour la fonction de distance que nous rencontrons dans l'espace euclidien.
L'espace métrique M est donc défini comme le
couple ordonné de (X, d). Certaines des fonctions métriques couramment
utilisées sont présentées ci-contre.
|
Distance euclidienne
Distance de Manhattan
Distance de Minkowski
|
|
Voir Propriété commutative / inégalité triangulaire / distance Manhattan
|
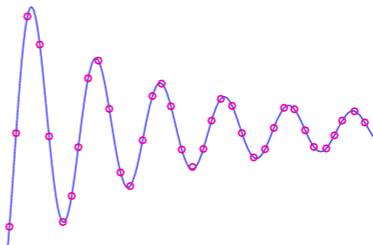
La suite de Cauchy est essentiellement une suite convergente. C'est une suite dont les nombres se rapprochent
de plus en plus au fur et à mesure que la suite des nombres progresse. (Illustration). En gros, il existe deux éléments de la suite,
tels que la distance entre eux est très petite (aussi petite que l'on veut). Dans le contexte d'un espace métrique M = (X, d),
la suite Cauchy est définie comme la suite dont la distance devient de plus
en plus petite au fur et à mesure que la série progresse. La suite converge vers un élément de X. Un espace
métrique est dit complet si chaque suite
de Cauchy qui le compose converge vers un élément de X. |
Allure sinusoïdale amortie
convergente vers zéro
Formule de la distance Étant donné m, n > N (un entier positif), on
a:
|
|
Suite de Cauchy –
Définition mathématique
|
On dit qu'une suite un de nombres réels ou de nombres
complexes est une suite de Cauchy si:
On lit: quel que
soit epsilon strictement positif, il existe un nombre entier N tel que, quels
que soient p et q supérieurs ou égaux à N, la distance entre les éléments p
et p de la suite est inférieure à epsilon. |
Convergence et
complétude
|
L'espace le plus important en algèbre linéaire de
base est Alors, un élément typique est un vecteur à n
éléments de nombres réels. Certaines opérations peuvent être réalisées avec
de tels vecteurs: addition, calcul de l'angle entre deux vecteurs, trouver la
limite des suites de vecteurs. Pour généraliser cela, nous souhaitons prendre
une liste infinie de coordonnées: (a1, a2, a3,…). Nous pouvons additionner de tels objets sans
difficulté. Si nous voulons trouver l'angle entre deux vecteurs, nous pouvons
essayer de calculer le produit scalaire:
La difficulté est que ce produit peut ne pas
converger. Pour s'assurer qu'il converge, nous devons exiger que les deux
suites ai et bi soient telles que:
Alors le produit scalaire sera fini et l'angle
pourra être calculé:
Longueur et angles sont maintenant définis. En ce qui concerne la suite des vecteurs de
dimension finie, elle converge vers un vecteur particulier si les longueurs
de leurs différences par rapport à ce vecteur tendent vers 0. L'important est que, tout comme pour les nombres
réels et l'espace euclidien, toute suite de Cauchy dans cet espace converge
réellement, en d'autres termes, l'espace devient complet. |
|
Norme La norme est une fonction qui indique la longueur
(valeur positive) de chaque vecteur d'un espace vectoriel (sauf le vecteur
nul). Il est généralement noté ||x||. Normé Un espace vectoriel normé est un espace métrique
dont la distance est définie comme la longueur du vecteur différence: d(x, y)
= ||x – y||. Note: tout
espace normé est à la fois un espace topologique linéaire et un espace
métrique. Un exemple parfait de l'intersection entre l'espace linéaire et
topologique. |
Définition générique d'une norme
Pour p = 1, c'est la norme absolue et Espace de Banach: un espace
vectoriel normé particulier. L'espace de Banach est un espace vectoriel
linéaire normé complet. |
|
|
Les espaces préhilbertiens introduisent une nouvelle
structure connue sous le nom de produit
scalaire. Il s'agit d'un opérateur mathématique qui agit
sur deux vecteurs pour produire un scalaire
(un nombre). Les produits scalaires ajoutent une structure
importante aux espaces métriques, car l'orthogonalité et l'angle entre les
vecteurs peuvent maintenant être calculés. Par conséquent, il s'agit d'un type d'espace
vectoriel normé (il ne satisfait cependant pas à la complétude). Les espaces préhilbertiens sont un excellent
moyen de généraliser les espaces euclidiens. Il est en effet facile
d'extrapoler les principes de base à des vecteurs de dimension supérieure. |
En mathématiques, un espace préhilbertien est
défini comme un espace vectoriel réel ou complexe muni d'un produit scalaire.
Cette notion généralise celles d'espace euclidien
ou hermitien dans le cas d'une dimension quelconque, tout en conservant
certaines bonnes propriétés géométriques des espaces de dimension finie grâce
aux propriétés du produit scalaire, mais en perdant un atout de taille :
un espace préhilbertien de dimension infinie n'est pas nécessairement
complet. On peut
cependant le compléter, pour obtenir un
espace de Hilbert. |
|
|
L'espace de Hilbert est un espace préhilbertien
qui satisfait la complétude. L'espace de Hilbert le plus simple est formé de
vecteurs indexés par des nombres. D'autres sont définis en indexant d'autres
objets mathématiques, comme des fonctions. Dans le cas de fonctions, la métrique est
l'intégrale du produit de deux fonctions. |
Distance en espace de Hilbert La structure supplémentaire qui le rend complet
est l'introduction d'une fonction de distance définie par:
|
|
|
Application en mécanique quantique La notion d'espace de Hilbert est essentielle aux
travaux de Hermann Weyl et John von
Neumann sur l'équivalence mathématique entre la mécanique matricielle de Heisenberg
et l'équation
de Schrödinger, ainsi qu'à la formulation générale de la mécanique
quantique. En physique quantique, une particule est
considérée comme un objet localisé dans un espace physique, c'est-à-dire un
espace euclidien tridimensionnel. La particule est décrite en termes d'états,
d'observables ou de valeurs probables, celles-ci sont données par des
vecteurs dans l'espace de Hilbert. Ainsi, cet espace aide à trouver la densité de
probabilité d'une particule quantique dans l'espace. |
Pourquoi l'espace de Hilbert L'espace euclidien pourrait réaliser presque
toutes les fonctions, mais il est limité en termes de dimensions, L'espace euclidien est un espace de dimension finie,
tandis que l'espace de Hilbert est une extension de l'espace euclidien et il
est de dimension infinie. Autres applications
|
|
Un des
propriétés des espaces de Hilbert
|
Principe minimum Si H est un espace de Hilbert, et E en est un sous-ensemble
fermé, convexe et non vide, alors E a un élément de norme minimale. Ce n'est
pas vrai dans un espace classique. Pour information, alors qu'il travaillait dans le
domaine des équations différentielles partielles, Riemann a supposé que le principe
minimum était vrai dans un espace non-Hilbert, jusqu'à ce que Weierstrass donne
un contre-exemple. |
Lecture
(d'après un texte anglais)
|
Bien sûr, on
peut effectuer des calculs sans définir l'espace vectoriel et sans traiter le
produit scalaire. Cependant, la notion d'espace
complet est indispensable à la théorie générale, tout comme la
complétion des nombres rationnels
pour obtenir les nombres réels
est critique. Le besoin du concept d'espace complet de fait sentir lorsqu'on
commence à effectuer des itérations pour résoudre une équation. Il est gênant
de ne pas avoir de limite pour la suite. En effet, de nombreux théorèmes des
espaces complets sont faux dans les espaces incomplets. Ce concept est
sans doute le plus important des mathématiques modernes. Avant cela, personne
n'avait réussi à proposer une définition cohérente du nombre réel. Les
équations, qui n'ont pas de solutions dans le domaine rationnel, peuvent en
avoir en nombres réels. Au début du XIXe
siècle, Cauchy examinait des suites de nombres rationnels qui convergent bizarrement
sur elles-mêmes (désormais appelées suites de Cauchy). En fait, il était
embarrassé par de telles suites. C'est à la fin
du XIXe siècle que Cantor a utilisé les suites de Cauchy pour définir un
nombre réel. Ce qui lui a permis de formuler les axiomes fondant les
mathématiques des ensembles. Les mathématiques s'en trouvent révolutionnées.
L'ère de la rigueur est née. Pour la première fois, les mathématiciens peuvent définir un nombre
réel d'une manière qui s'est étendue très généralement à d'autres types de
paramètres tels que les espaces de produits scalaires et les espaces normés. Ainsi, la
construction de Cantor, utilisée pour les réels, pouvait facilement être
étendue aux espaces vectoriels en définissant une métrique telle qu'une
norme, ce qui a rapidement conduit à la notion d'espace de Hilbert. Des suites de
fonctions orthogonales obtenues en résolvant des équations de math et de
physique pourraient désormais avoir des limites abstraites, et non, seulement
converger sur elles-mêmes. Par exemple, des
problèmes impliquant le principe de Dirichlet, pouvaient désormais donner des
solutions réelles dans un contexte très général. Les processus
itératifs produisaient des suites vers lesquelles converger. Bien sûr, les
objets considérés comme des solutions devaient être des objets non classiques
dans un espace particulier comme Hilbert ou Banach. Cela a conduit
pour la première fois à des résultats d'existence générale pour les équations.
Et cela a permis de penser à des espaces où les points pourraient être des
objets compliqués tels que des fonctions, et de définir la distance et la
proximité topologique pour de tels points. Les mathématiques modernes n'auraient
pas progressé autant sans une telle abstraction. Les espaces
vectoriels abstraits munis d'une topologie sont l'évolution naturelle des
efforts des mathématiciens pour résoudre les équations des mathématiques et de
la physique. |
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
Hilbert contemporain