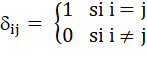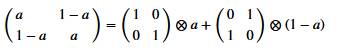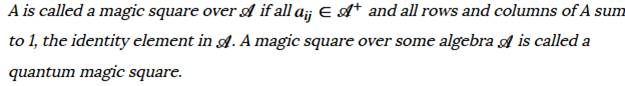NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 27/11/2020

Orientation générale        DicoMot Math          Atlas                   Actualités                       M'écrire

Barre de recherche          DicoCulture              Index alphabétique        Références      Brèves de Maths

      

OUTILS

 

Débutants

MATRICE

MATRICES

 

Glossaire

Général

 

 

INDEX

 

Matrices

 

Outils 

 

Introduction

Addition

Multiplication

Puissance

Formes

Déterminant

Inversion

Historique

 

Sommaire de cette page

>>> Matrices particulières

>>> Opposée

>>> Transposée

>>> Canonique

 

 

 

 

MATRICES – Formes particulières

 

Diverses matrices autour de la même matrice de départ

1

2

 

1

3

3

4

 

2

4

 

Matrice transposée

Rappel

Une matrice est dite carrée si elle comporte autant de lignes que de colonnes. Sinon, elle est rectangulaire.

Voir Débutants / Novices

 

 

Matrices PARTICULIÈRES

 

*   NULLE

(0 – matrix)

 

 

 

0

0

0

0

0

0

0

0

0

0

0

0

  

*   UN

(Unit matrix)

 

 

1

1

1

1

1

1

1

1

1

1

1

1

 

 

 

*   UNITÉ (carrée)

(Identity matrix)

Avec le symbole de Kronecker

La matrice unité I s'écrit

I  =   ( )

 

 

 

1

0

0

0

0

1

0

0

0

0

1

0

0

0

0

1

*   DIAGONALE (carrée)

(Diagonal matrix)

 

a

0

0

0

0

b

0

0

0

0

c

0

0

0

0

d

 

*   SCALAIRE (carrée)

(Scalar matrix)

 

a

0

0

0

0

a

0

0

0

0

a

0

0

0

0

a

 

*   SYMÉTRIQUE (carrée)

(Symmetric matrix)

Le nombres sur la diagonale principale peuvent être tous différents.

Une matrice diagonale est symétrique.

 

a1

b

c

d

b

a2

e

f

c

e

a3

g

d

f

g

a4

 

 

*   ANTISYMÉTRIQUE (carrée)

(Antisymmetric or skew-symmetric matrix)

Matrice symétrique dont les valeurs symétriques par rapport à la diagonale principale sont les valeurs opposées.

Notez les 0 sur la diagonale.

Une matrice antisymétrique est opposée à sa transposée.

 

 

 

0

b

c

d

-b

0

e

f

-c

-e

0

g

-d

-f

-g

0

 

*   TRIANGULAIRE (supérieure ou inférieure)

(Upper and lower triangular matrix)

 

 

a

b

c

d

0

e

f

g

0

0

h

i

0

0

0

j

 

 

 

*  STOCHASTIQUE

Formée de nombres réels dont la somme sur chaque ligne vaut 1.

 

*  BISTOCHASTIQUE

Formée de nombres réels dont la comme sur chaque ligne et chaque colonne vaut 1.

Utilisation en probabilités et combinatoire.

Une des propriétés:

 

 

0,1

0,3

0,3

0,3

0

0

0,5

0,5

0,1

0,1

0,1

0,7

0,2

0,2

0,2

0,4

 

1

0

0

0

0

1

0

0

0

0

1

0

0

0

0

1

 

 

*  Quantum magic square**

Matrice bistochastique dont chaque élément est tout élément arbitraire de l'algèbre non-commutative.

Voir Carrés magiques – Index

 

 

 

MATRICE OPPOSÉE

*   Matrice négative de celle d'origine

1

2

=> -

1

2

=

-1

-2

5

6

5

6

-5

-6

 

Matrice initiale              Matrice opposée

M                         - M

 

 

Matrice TRANSPOSÉE

*   Les lignes deviennent colonnes

*   Les colonnes deviennent lignes

 

NB

-          La transposée d'un vecteur-ligne est un vecteur-colonne

-          La transposée d'un vecteur-colonne est un vecteur-ligne

1

2

3

4

 

1

5

9

5

6

7

8

 

2

6

10

9

10

11

12

 

3

7

11

 

 

 

 

 

4

8

12

 

Matrice initiale              Matrice transposée

M                          M t

 

 

 

Matrice CANONIQUE

 

*   Décomposition en somme de matrices

dont les coefficients sont tous nuls

sauf celui correspondant au rang du coefficient multiplicatif de la matrice d'origine

 

a

b

= a x

1

0

c

d

0

0

 

 

 

 

 

 

 

+ b x

0

1

 

 

0

0

 

 

 

 

 

 

 

+ c x

0

0

 

 

1

0

 

 

 

 

 

 

 

+ d x

0

0

 

 

0

1

 

 

 

 

 

 

SUITE

* Déterminant

Voir

* Équations

* Outils mathématiques

* Théorie des nombres

Sites

* Matrice (mathématiques) - Wikipédia

* Matrice – Résumé des cours – BibM@th.net

* Matrix -- from Wolfram MathWorld

Cette page

http://villemin.gerard.free.fr/aMaths/Outils/Matrice/Forme.htm