|
Édition du: 04/01/2020 |
|
INDEX |
Graphes – Coloriage |
|||
![]()
|
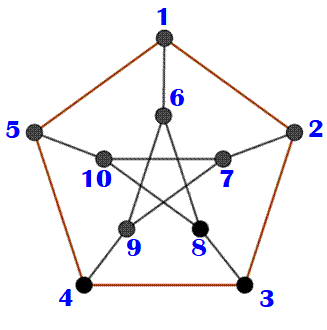
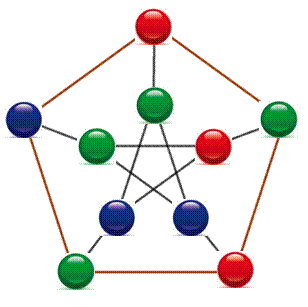
Colorier ce graphe en double pentagone |
||
|
|
Sommaire de cette page >>> Le défi >>> Méthode de résolution |
Débutants Glossaire |
|
Énigme Le défi consiste
à colorier chacun des dix sommets de ce graphe de sorte que deux sommets
réunis par un segment soit de couleur différente. Dit-autrement chacun
des quinze segments doit être terminé par deux couleurs différentes. Remarque Si on donne la
couleur rouge au somment 1, il faut donner une couleur différente au sommet 2
et au sommet 5. Ces deux sommets, 2 et 5, pouvant être de la même couleur ou
de couleurs différentes. |
|
||||
|
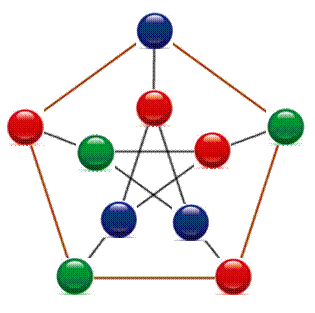
Solution On montre tout
de suite une des solutions. Elle nécessite
trois couleurs, mais pas plus. On a bien des
extrémités de couleurs différentes:
|
|
||||
|
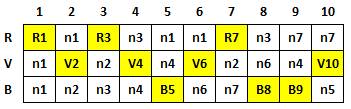
Connexions des sommets On donne le nom
du sommet suivi de la liste des sommets qui lui sont reliés:
Il s'agit
maintenant de faire des choix et de trouver les compatibilités. On utilise trois
listes, une par couleur: R, V et B. |
|
|||
|
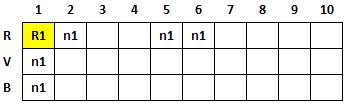
On attribue la couleur Rouge (R1) au sommet n°1.
Alors ce même sommet n'est ni Vert, ni Bleu en colonne 1 (n1 = non-possible
du fait de la première opération). On poursuit en indiquant que Rouge en peut pas
être en [2, 5, 6] conformément au
relevé de connexions. |
|
|||
|
Nous poursuivons le remplissage en excluant à
chaque fois les impossibilités. Chacune des actions est indicée pour
reconnaitre leur origine. Les choix de couleur est parfois arbitraire (V2
aurait pu être B2). Ce qui induit plusieurs solutions. |
|
|||
|
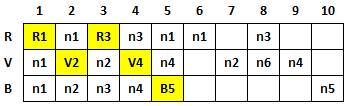
En poursuivant, et après essais-erreurs pour éviter
les cas impossibles, on arrive à ce tableau qui représente l'une des
solutions |
|
|||
|
Le graphe représente la disposition trouvée. Évidemment, il est possible d'arriver à l'une de
ces solutions par tâtonnement. Cependant, la méthode permet de trouver toutes
les solutions en modifiant les choix opérés en établissant le tableau. Toutes les configurations par rotations et
symétrie sont également valables; de même que par échange des couleurs. Il existe également certains échanges possibles
comme 1B, 5 B et 6V qui donnent la configuration présentée en tête de cette
page. |
|
|||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |