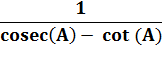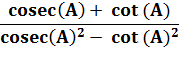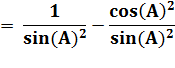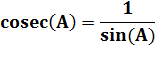|
||||||||||||||||||||||||||||||||||||||||
![]()
|
RELATIONS TRIGONOMÉTRIQUES Découverte d'une
formule par le biais d'un problème classique.
|
Rappel
|
Cosécante
(A) = 1 / sin (A) Cotangente (A) = cos (A) / sin (A) |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
(a – b) (a + b) |
= a² – b² |
|
|
|
|
= 3 |
|
|
|
|
= 3 |
|
|
|
|
|
|
|
|
|
= 3 |
|
|
|
|
|
|
|
|
A |
= 0,6435 … radian = 36°,87… |
|
![]()
|
Bases |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Trigonom/aaaBases/Cosecant.htm |
![]()