|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
CALCULS EN TRIGONOMÉTRIE – 01 Produits
de six cosinus égal à une fraction. Produits
de sept sinus égal à une fraction. |
|
|
||
|
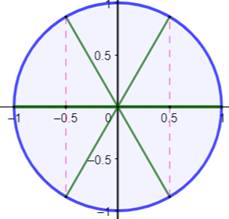
Problème Calculer ce produit sachant que cos(a) cos(2a) cos(3a) (cos4a) (cos5a) (cos6a) Solution La réponse se lit sur le cercle trigonométrique. Les rayons verts représentent les angles de valeurs
successives: 60°, 120°, 180°, … Les cosinus de ces angles sont les segments sur
l'axe horizontal: 1/2 , -1/2 , -1,
-1/2, 1/2, et 1. Leur produit avec ces trois valeurs négatives est
négatif et il vaut: -1/16 |
|
|
Voir Brève
770 / Identités de ce type
|
|
||
Problème
Quelle est la valeur de
l'expression, produit de sept sinus? |
E =
sin( sin( 3 sin( 5 sin( 7 sin( 9 sin(11 sin(13 |
|
Valeur numérique
Calcul numérique pour apprivoiser
l'expression et savoir où nous mettons les pieds. Observez la symétrie et la valeur
centrale égale à 1. |
E = 0,22252093 x 0,6234898 x 0,90096887 x 1 x 0,90096887 x 0,6234898 x 0,22252093 = 0,015625
= 1/64 |
|
Calcul
Cherchons à exploiter la symétrie
dans l'expression de E. Exprimons d'abord la valeur des
facteurs extrêmes. De même: |
13 13 13 sin(13 sin(13 sin(11 sin( 9 |
|
|
Quant la valeur centrale: |
7 sin( |
|
|
On peut écrie E de la façon
suivante: |
E = sin( sin( = { sin( = K² |
|
|
Reste à évaluer la valeur de k. |
K = sin( |
|
|
Essayons de diviser le dénominateur
par deux en faisant intervenir |
Relation générale sin( Application sin( = cos(6 sin(3
= cos(4 sin(5
= cos(2 |
|
|
Où en sommes-nous? Calcul à la calculette pour savoir
ce qu'il faut trouver. |
K = cos( K = 0,124999999… |
|
![]()
Calcul littéral (suite)
L'astuce
ici est de forcer l'utilisation de l'angle double. Quitte à
introduire une fraction unitaire en sinus pour obtenir une expression en
sin.cos En
cascade, nous obtenons encore une expression en sin.cos En
remarquant que 3 À nouveau
une expression en sin.cos En notant
que La valeur
de K est connue. |
K = cos( Relation générale sin(2 sin( Application
1/64 = 0, 015625 |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
![]()