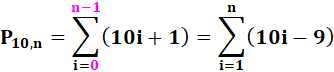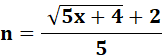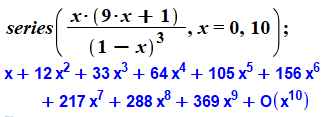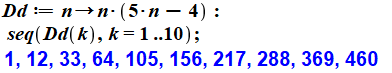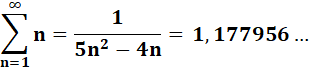|
Édition du: 21/06/2020 |
|
INDEX Types de nombres figurés: liste
et liens |
Nombres Polygonaux |
|||
![]()
|
NOMBRES DODÉCAGONAUX 12-gonal Nombres
construits en déposant des points sur des décagones gigognes, chacun appuyé sur le précédent. |
||
|
|
Sommaire de cette page >>>
Nombres décagonaux >>>
Nombres décagonaux – Tables >>>
Propriétés avec les nombres triangulaires >>>
Nombres décagonaux généralisés |
Débutants Nombres
figurés ou
géométriques Glossaire |
|
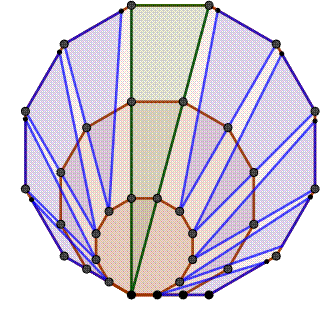
Construction des nombres
dodécagonaux
Observez que le
supplément (gnomon) est en 10n
+ 1. |
|
|||||||||||||||||||||||||||||
|
Notation et formules La formule en somme
résulte du décompte vu ci-dessus. L'incrément étant égal à: 10n + 1 |
|
|||||||||||||||||||||||||||||
|
Caractérisation Sorte de racine dodécagonale. |
Si
n est un nombre entier alors x est le énième nombre dodécagonal. Sinon, il n'est
pas hexagonal. N
est une des racines de x = 5n² – 3n |
|||||||||||||||||||||||||||||
|
Fonction génératrice L'instruction demande le développement sur dix
termes. |
|
|||||||||||||||||||||||||||||
|
Programme |
|
|||||||||||||||||||||||||||||
|
Somme des inverses des dodécagonaux |
|
|||||||||||||||||||||||||||||
|
Nombres
décagonaux – Tables |
||
|
Les 100 premiers dodécagonaux |
1, 12, 33, 64, 105, 156, 217, 288, 369, 460, 561,
672, 793, 924, 1065, 1216, 1377, 1548, 1729, 1920, 2121, 2332, 2553, 2784,
3025, 3276, 3537, 3808, 4089, 4380, 4681, 4992, 5313, 5644, 5985, 6336, 6697,
7068, 7449, 7840, 8241, 8652, 9073, 9504, 9945, 10396, 10857, 11328, 11809,
12300, 12801, 13312, 13833, 14364, 14905, 15456, 16017, 16588, 17169, 17760,
18361, 18972, 19593, 20224, 20865, 21516, 22177, 22848, 23529, 24220, 24921,
25632, 26353, 27084, 27825, 28576, 29337, 30108, 30889, 31680, 32481, 33292, 34113,
34944, 35785, 36636, 37497, 38368, 39249, 40140, 41041, 41952, 42873, 43804,
44745, 45696, 46657, 47628, 48609, 49600 |
|
|
Dodécagonaux carrés |
1, 64,
3025, 142129, 6677056, 313679521, 14736260449, 692290561600 |
|
|
P12,n = Tn + 9Tn-1 = 1/2 n (n + 1) + 9/2 (n – 1) n = 1/2 (n² + n + 9n² – 9n) = 5n² – 4n |
|
|
|
Dodécagonaux du deuxième ordre |
Même
formule que pour les ordinaires avec signe plus. |
|
|
Les premiers dodécagonaux du 2e
ordre |
9, 28, 57, 96, 145, 204, 273, 352, 441, 540, 649,
768, 897, 1036, 1185, 1344, 1513, 1692, 1881, 2080, … |
|
|
Dodécagonaux généralisés |
Soit la réunion des nombres décagonaux ordinaires
avec les centrés. |
|
|
Les premiers dodécagonaux
généralisés (ordinaires et du 2e ordre) |
1, 9, 12, 28, 33, 57, 64, 96, 105, 145, 156, 204,
217, 273, 288, 352, 369, 441, 460, 540, 561, 649, 672, 768, 793, 897, 924,
1036, 1065, 1185, 1216, 1344, 1377, 1513, 1548, 1692, 1729, 1881, 1920, 2080,
2121, … |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |