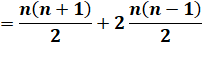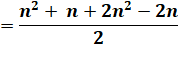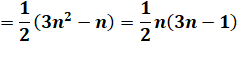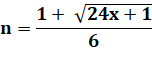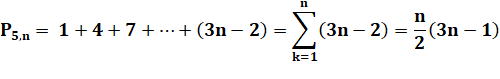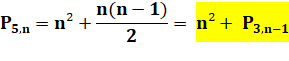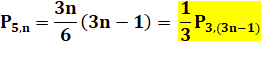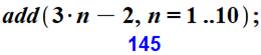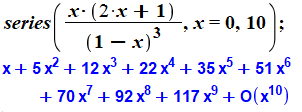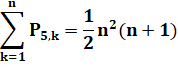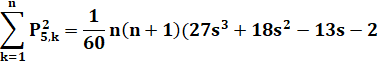|
Édition du: 10/04/2021 |
|
INDEX Types de nombres figurés: liste
et liens |
Nombres Polygonaux |
|||||
|
|
||||||
|
|
|
|||||
![]()
|
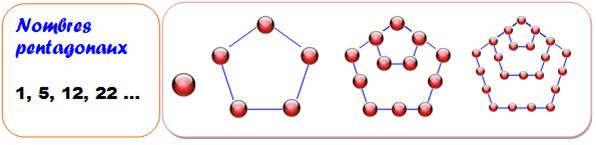
NOMBRES PENTAGONAUX Nombres
construits en déposant points sur des hexagones gigognes. L'un dans l'autre,
mais avec deus côtés communs. |
||
|
|
Sommaire de cette page >>> Caractéristiques >>> Liste >>> Pentagonaux = Somme
de pentagonaux |
Débutants Nombres figurés
ou géométriques Glossaire |
|
NOMBRES PENTAGONAUX Nombres pentagonaux (P5, n)
:
|
|
|
|||||
|
Famille |
|
||||
|
Définitions |
NOMBRE PENTAGONAL (ordinaire ou du premier ordre) Nombre
formé à partir d'un pentagone et d'autres pentagones internes. Le
nombre est le cumul de tous les |
||||
|
Formule |
|
||||
|
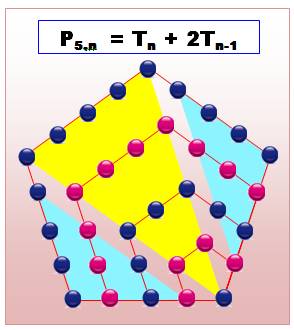
Calcul de la formule |
Cette
figure montre comment relier le nombre pentagonal aux nombres
triangulaires.
|
|
|||
|
|
Calcul
avec formule ½
(3 x 7² – 7) = ½ (147 – 7) = ½ (140) = 70 Calcul
des aires 7²
+ 7x6/2 = 49 + 21 = 70 |
|
|||
|
Test |
Le
réel x positif est pentagonal s'il est
racine de l'équation: 3n² – n – 2x = 0.
Lorsque ce nombre réel n est un entier
alors x est le énième pentagonal. Autre
test Vérifier
que 24x + 1 est un carré et que (24x + 1)1/2 vaut 5 mod 6. |
||||
|
Avec les triangulaires |
P5,n = 1/3 T3n-1
= 1/3 x 1/2
(3n–1)(3n) = 1/2 n(3n – 1) = 3 Tn-1 + n = 3 x 1/2 x (n–1)n + n = 3/2 x n² – 1/2 x n = Tn-1 + n² |
|
|
Autres formulations |
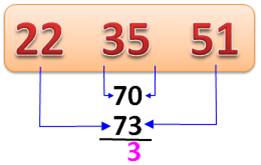
Progression
arithmétique de raison 3n – 2 Chaque
nombre de la progression représente le complément à la couche pentagonale
précédente. Chaque
couche comporte: 5(n – 1) points.
Carré de
n +
triangulaire
d'ordre n (Voir
figure ci-dessus pour 7) Exemple: P5,5
= 5² + 5x4/2 =35 |
|
|
|
Un tiers
du triangulaire d'ordre 3n – 1 Récurrence
Exemple
|
|
|
Propriétés |
Théorème: tous les
nombres sont somme de cinq nombres pentagonaux Conjecture: seuls 6 nombres ne sont pas somme de
quatre nombres pentagonaux. Vérifié au moins pour ces six
valeurs. |
Non somme de un à quatre pentagonaux 9, 21, 31, 43, 55 et 89 |
|
|
Exemple de calcul avec logiciel |
|
||
|
Fonction génératrice |
Voir Fonctions
génératrices des polygonaux |
||
|
Somme |
|
Exemple: n = 4 1 + 5 + 12 + 22 = 40 4² x 5 / 2 = 40 |
|
|
Somme des carrés |
|
Exemple: n = 4 1² + 5² + 12² + 22² = 654 1/60 x 4 … = 654 |
|
|
Anglais Allemand |
Pentagonal number Fünfeckszahl oder
Pentagonalzahl |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
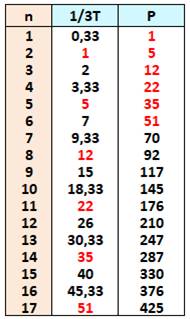
Nombres
pentagonaux pour n de 0 à 99 Exemple:
P5,
21 = 651
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Voir Carrés / Cubes / Palindromes
|
|
||
|
Exemple P5,4
+ P5,7 = P5,8 22 + 70 =
92 |
[4, 7, 8], [5, 5, 7], [7, 23, 24], [10, 48, 49],
[12, 22, 25], [13, 82, 83], [14, 47, 49], [17, 26, 31], [17, 70, 72], [19,
22, 29], [20, 37, 42], [21, 71, 74], [25, 26, 36], [28, 52, 59], [28, 95,
99], [33, 87, 93], [35, 72, 80], [36, 67, 76], [37, 63, 73], [39, 57, 69],
[42, 51, 66], [44, 82, 93], [45, 47, 65], [65, 68, 94] |
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()