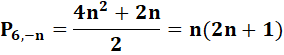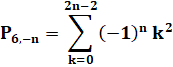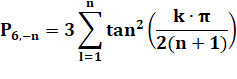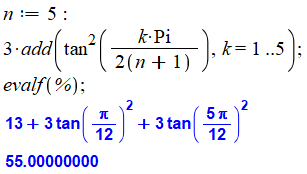|
Édition du: 18/06/2020 |
|
INDEX Types de nombres figurés: liste
et liens |
Nombres Polygonaux |
|||
|
Hexagonaux de 2e
ordre et généralisés |
||||
![]()
|
NOMBRES HEXAGONAUX de deuxième ordre Nombres
construits sur le même modèle que les nombres hexagonaux ordinaires en
changeant le signe. |
||
|
|
Sommaire de cette page >>> Approche >>> Propriétés avec les entiers >>> Propriétés avec le triangle de Pascal >>> Propriétés avec les carrés >>> Propriétés avec la trigonométrie |
Débutants Nombres figurés
ou géométriques Glossaire |
|
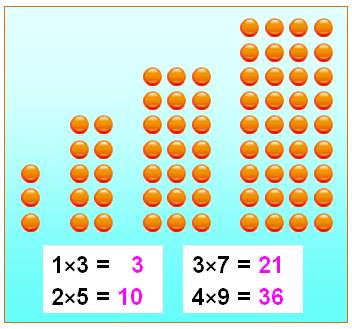
Illustration Nombres déduits des nombres hexagonaux par un
changement de signe. Nombres rectangulaires voisins des nombres
proniques. |
|
||
|
Notation et formule |
|
||
|
Les
premiers |
0, 3, 10, 21, 36, 55, 78, 105, 136, 171, 210, 253, 300, 351, 406, 465,
528, 595, 666, 741, 820, 903, 990, 1081, 1176, 1275, 1378, 1485, 1596, 1711,
1830, 1953, 2080, 2211, 2346, 2485, 2628, 2775, 2926, 3081, 3240, 3403, 3570,
3741, 3916, 4095, 4278, … |
||
|
Les
nombres hexagonaux sont la somme des nombres impairs en 4k – 1. |
Exemple
|
|
|
Différences
entre une succession de nombres pairs
et de nombres impairs. Exemples 8
+ 10 + 12 – 1 – 3 – 5 = 21 10
+ 12 + 14 + 16 – 1 – 3 – 5 – 7 = 36 Note: voir la disposition en escalier produisant ces nombres hexagonaux
du 2e ordre. |
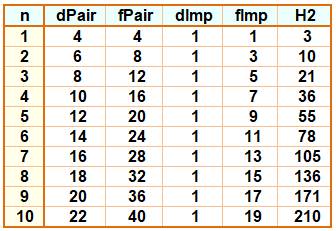
Table (dPair
= début pair, fPair = fin pair …)
|
|
|
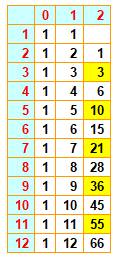
Les
nombres hexagonaux du 2e ordre sont les coefficients du
binôme: combinaisons de 2 parmi 2n + 1. Les hexagonaux ordinaires sont les autres nombres
de la même colonne Programme
|
Extrait du triangle
de Pascal |
||
|
Formule
Exemple
|
|
||
Voir Triangle de Pascal
– Table
|
Somme
alternée de carrés |
Exemple
|
|
|
Ces
nombres hexagonaux (H) sont le point de départ d'une suite infinie d'égalités
de sommes de carrés. Voir Brève
de maths 503 |
H² + (H+1)² + …+ (H+n)² = (H+n+1)²+ … (H+2n)²
Voir Égalités
semblables avec les hexagonaux ordinaires |
|
|
Curiosité
trigonométrique
|
Exemple avec 5
|
|
|
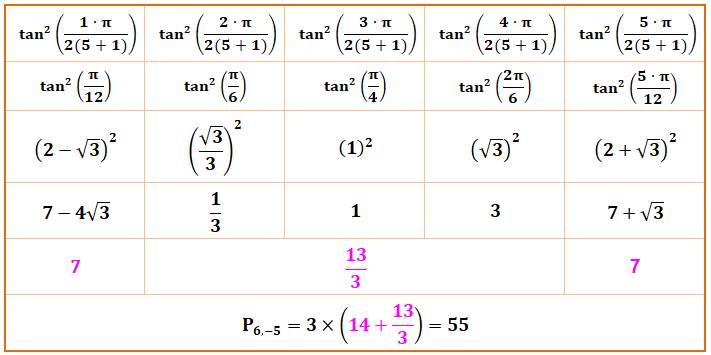
Détail du calcul avec n = 5
|
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |