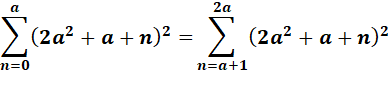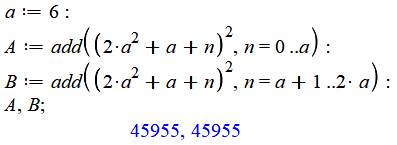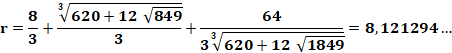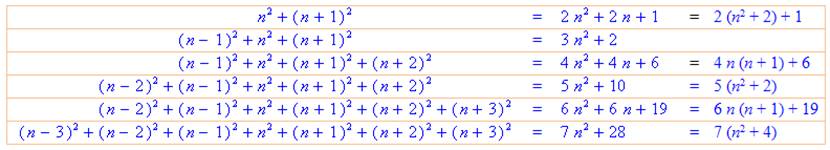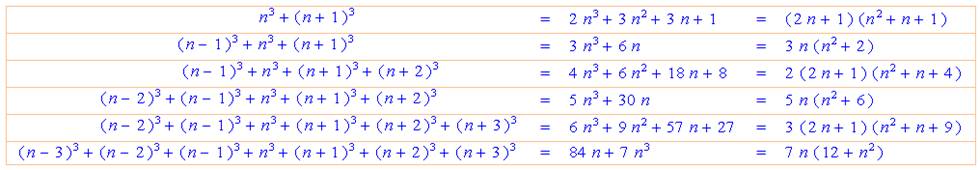|
|||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
CARRÉS et PUISSANCES Somme des carrés
des nombres consécutifs. En partant de 1, ce
sont les nombres pyramidaux carrés: 1² + 2² + 3² = 14 1² + 2² + 3² + 4² = 30 1² + 2² + 3² + 4² + 5² = 55 … Pour commencer une
propriété stupéfiante, mais qui s'explique très bien. |
|
|
||
|
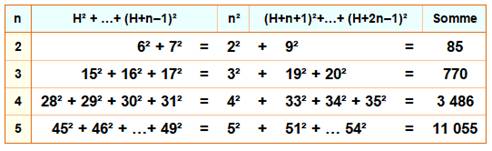
Égalité
sans fin entre somme de carrés
La
valeur du
nombre avant le signe égal vaut: 2n
(n + 1) = 4Tn
avec n le rang de l'égalité. Le nombre de départ vaut n (2n + 1), les nombres
hexagonaux du deuxième ordre Voyons
cela: |
||
|
Somme de deux carrés de nombres consécutifs = carré. Le nombre central est 4 avec 3 carrés. |
Mise en équation (n – 1)² + n² = (n + 1)² n² – 2n + 1 + n² = n²
+ 2n + 1 n² – 4n = n(n – 4) =
0 => n = 0 ou 4 Seule solution non
triviale: 3² + 4² = 5² = 25 |
|
|
Somme de trois carrés de nombres consécutifs = somme de deux
carrés. Le nombre central est C = 12 avec 5 carrés. Le nombre 5 est impair: 5 = 2k + 1 avec k = 2 Avec k, on a: |
(n – 2)² + (n – 1)² + n² –
(n + 1)² – (n + 2)² = 0 n² – 4n + 4 + n² – 4n
+ n² + 4n + 4 = 0 Les termes extrêmes du
développement des nouveaux carrés s'éliminent. Seuls subsistent les termes
centraux en 4n. n² – 4n – 4n – 4n = 0 n² – 12n = 0 n = 12 Seule solution non
triviale: 10² + 11² + 12² = 13² +
14² = 365 |
|
|
Autres égalités
remarquables du même type.
|
|
|
|
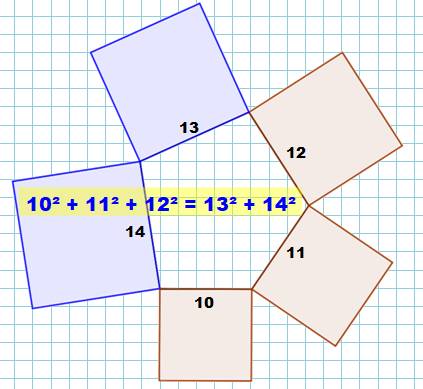
Illustration des sommes
avec cinq carrés Aire des carrés bleus = aire des carrés roses
|
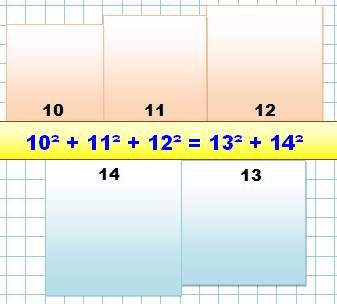
Disposition propice à
un exercice Quatre terrains carrés dont les côtés sont des
nombres consécutifs et les superficies sont égales de part et d'autre du
chemin. Trouvez ces nombres.
|
|
Somme de quatre carrés … Avec k = 3, on a: |
(n – 3)² + n² – 12n
– (n + 3)² = 0 n² – 12n – 6n – 6n = n² – 24n =
0 21² +22² + 23² + 24² =
25² + 26² + 27² = 2 030 |
|
|
Somme de 2k + 1 carrés … Avec k, on a |
(C – k) + … + C² = (C +
1)² + … (C + k)² |
|
|
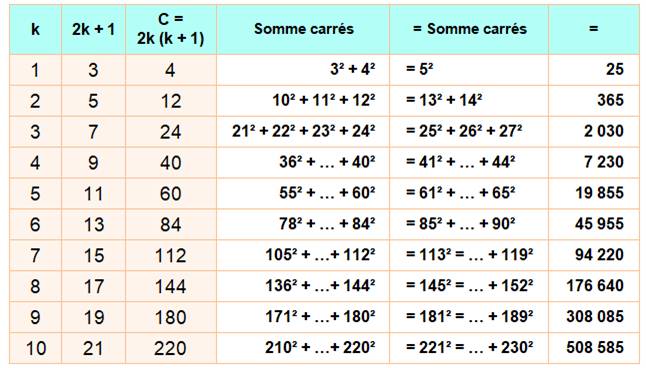
Les 10
premières égalités de sommes de carrés successifs Si
C est le nombre central, il y a autant de nombres de chaque côté de C.
Note: on aurait bien évidemment les mêmes résultats
en progressant de 2 en 2 ou de r en r. Ex: r = 2 : 20² + 22² + 24² = 26² + 28² ; r = 3 :
30² + 33² + 36² = 39² + 42². |
||
|
|
Programme Maple Redémarrage Boucle
d'analyse avec k prenant successivement les valeurs de 1 à 5. Calcul
du nombre central C et des deux sommes La
première somme
se lit: additionner les termes C – 1 + i pour toutes les valeurs de i allant
de 0 à k. Imprimer
les bornes de l'égalité, et les deux sommes. On vérifie qu'il s'agit bien de
la même somme. Fin
de boucle avec do (faire) à l'envers. Impression
du résultat de traitement en bleu. |
|
Voir Triplet
de Pythagore le plus célèbre / Pépites
/ Table
des sommes de carrés de nombres consécutifs /
Triplets de Pythagore dont la somme des
deux termes est un carré
|
|
|||
|
Formule |
|
||
|
Notation
linéaire (Maple) |
|
||
|
Exemple
a = 2 |
a
= 2 2a²
+ a = 10 2a²
+ a + n = 10, 11, … (2a²
+ a + n)² = 100, 121, … Cumul:
100, 221, 365. |
|
|
|
Exemple
a = 6 |
a = 6 2a² + a = 78 2a² + a + n = 78, 79 … (2a² + a + n)² = 6084 … Cumul: 6084, 12325 … Total commun: 45 955 |
|
|
Avec des cubes ? Puissance 4 ?
|
Il
n'est pas possible de reproduire la même histoire avec des cubes. (n
– 1)3 + n3 – (n + 1)3 = n3 – 6 n2
– 2 = 0, avec la racine réelle:
En
effet: 5,054553 + 6,054553 = 7,054553 = 351,
081 … Même
topo avec la puissance 4 (n
– 1)4 + n4 – (n + 1)4 = n4 – 8 n3
– 8n = 0, avec la racine réelle (outre 0):
En
effet: 7,12124 + 8,12124 = 9,12124 = 6
921,622… |
Merci à Maurice-Denis F.
pour m'avoir rappelé cette magnifique suite d'égalités
![]()
|
Sommes de 2, 3 ou 4 carrés Somme
des carrés de deux
termes consécutifs
Ex: 3² + 4² = 2 x 12 + 1
= 25 Somme
des carrés de trois
termes consécutifs
Ex: 3² + 4² + 5² = 3 x
16 + 2 = 50 Somme
des carrés de quatre
termes consécutifs
Ex: 3² + 4² + 5² + 6² = 4
x 20 + 6 = 86 |
|||||||||||||||||||||||||||||||||||||||
|
Sommes de 5, 6 ou 7 carrés Somme des carrés de cinq termes consécutifs
Ex: 3² + 4² + 5² + 6² +
7² = 5 x 5² + 10 = 135 Présentation symétrique
Ex: 3² + 4² + 5² + 6² +
7² = 5 x (5² + 2) = 135 Somme
des carrés de six
termes consécutifs
Ex: 3² + 4² + 5² + 6² +
7² + 8² = 6 x (5x6) +19 = 199 Somme
des carrés de sept
termes consécutifs
Ex: 3² + 4² + 5² + 6² +
7² + 8² + 9² = 7 x 6² + 28 = 280 |
||||||||||||||||||||||||||||||||
|
|
|
|
Voir TABLES |
|
Voir Partition en carrés
|
|
|
|
Voir TABLES |
|
Voir Partition en cubes
|
|
|
|
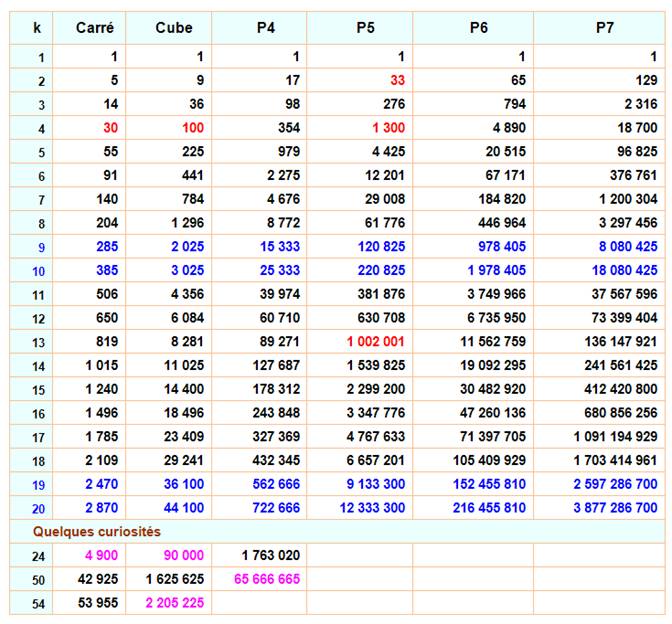
Principe Somme des puissances des nombres
consécutifs à partir de 1. Exemple pour une
quantité de 3 termes 1² + 2² + 3² = 14 13 + 23
+ 33 = 36 14 + 24
+ 34 = 98 … Table
Suite en Table
des puissances et leurs sommes |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()