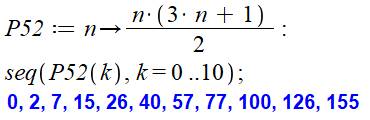NOMBRES - Curiosités, théorie et usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 18/06/2020

Orientation générale        DicoMot Math          Atlas                   Actualités                       M'écrire

Barre de recherche          DicoCulture              Index alphabétique        Références      Brèves de Maths

        

Nombres Figurés

 

Débutants

Nombres figurés ou géométriques

Nombres géométriques

 

Glossaire

Nombres

géométriques

 

 

INDEX

 

Types de nombres figurés: liste et liens

 

Nombres

 

 

Carrés

Pentagonaux

Hexagonaux

Autres

Penta de 2e ordre

Penta généralisé

Penta centrés

Penta Théorème

Penta en grappes

 

Sommaire de cette page

>>> Nombres pentagonaux du deuxième ordre

 

 

 

 

Nombres pentagonaux du deuxième ordre

 

Ce sont les nombres qui reprennent la formule des nombres pentagonaux ordinaires avec le signe plus.

 

 

P52, n = 1/2 (3n² + n)

 

 

La somme des n nombres consécutifs supérieurs à n est égale au nombre pentagonal du deuxième ordre d'ordre n.

 

 

 

S = 6 + 7 + 8 + 9 + 10 = 16 + 16 + 8 = 40

 

P52, 5 = (3x5² + 5) / 2 ) = 80 / 2 = 40

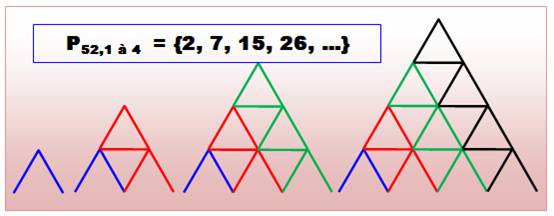
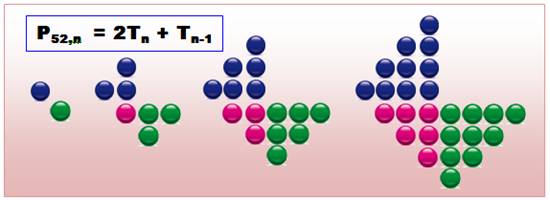
Illustrations

 

 

 

 

 

  

 

Récurrence

 

P52, n-1 = n + …. + 2n – 2

P52, n   =       n+1  + ….      + 2n–1 + 2n

E =  –n + 2n–1 + 2n = 4n – n – 1

 

P52, n  = P52, n-1 + 4n – n – 1

 

Programme Maple

 

Voir Programmation – Index

Trucs de programme

 

 

[n et 2-pentagonal]

 

[1, 2], [2, 7], [3, 15], [4, 26], [5, 40], [6, 57], [7, 77], [8, 100], [9, 126], [10, 155], [11, 187], [12, 222], [13, 260], [14, 301], [15, 345], [16, 392], [17, 442], [18, 495], [19, 551], [20, 610]

 

Les cent plus petits nombres pentagonaux du deuxième ordre

0, 2, 7, 15, 26, 40, 57, 77, 100, 126, 155, 187, 222, 260, 301, 345, 392, 442, 495, 551, 610, 672, 737, 805, 876, 950, 1027, 1107, 1190, 1276, 1365, 1457, 1552, 1650, 1751, 1855, 1962, 2072, 2185, 2301, 2420, 2542, 2667, 2795, 2926, 3060, 3197, 3337, 3480, 3626, 3775, 3927, 4082, 4240, 4401, 4565, 4732, 4902, 5075, 5251, 5430, 5612, 5797, 5985, 6176, 6370, 6567, 6767, 6970, 7176, 7385, 7597, 7812, 8030, 8251, 8475, 8702, 8932, 9165, 9401, 9640, 9882, 10127, 10375, 10626, 10880, 11137, 11397, 11660, 11926, 12195, 12467, 12742, 13020, 13301, 13585, 13872, 14162, 14455, 14751, 15050

 

Anglais: Second pentagonal numbers

 

 

Suite

*      Nombres pentagonaux généralisés

*      Nombres hexagonaux

*      Nombres en grappe pentagonale

*      Nombres pentagonaux, hexagonaux et suite

*      Nombres hexagonaux

Voir

*      Calcul des carrés

*      Caractérisation des nombres avec des premiers

*      Carré en géométrie

*      Nombres carrés – Glossaire

*      Nombres carrés – Index

*      Puissance – Index

*      Racine carrée – Calcul mental

*      Racine carrée d'un nombre – Glossaire

Sites

*      Nombre pentagonal – Wikipédia

*      Pentagonal Number – Wolfram MAthWorld

*      OEIS A000326 – Pentagonal numbers

*      OEIS A001318 – Generalized pentagonal numbers

*      OEIS A036353 – Square pentagonal numbers

*      OEIS A005449 – Second pentagonal numbers: a(n) = n*(3*n + 1)/2

*      Pentagonal Numbers: Representing Algebra Geometrically – Brilliant.org – Vidéo

Cette page

http://villemin.gerard.free.fr/aNombre/FIGURE/Penta2.htm