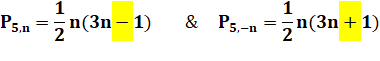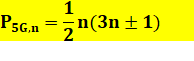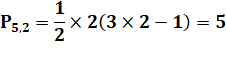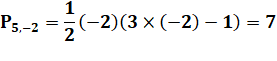|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
|
|||
|
Pentagonaux ordinaires + Pentagonaux du deuxième
ordre |
|
||
|
Définition |
Nombre de la
forme n (3n – 1) / 2 (même chose que
pour les nombres pentagonaux ordinaires), mais avec n prenant les valeurs
alternées: 0, +1, -1, +2, -2, … |
||
|
Exemples |
|
||
|
Liste |
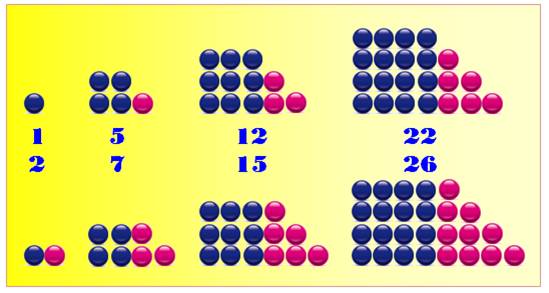
0, 1, 2,
5, 7, 12, 15, 22, 26, 35, 40, 51, 57, 70, 77, 92, 100, 117, 126, 145, 155,
176, 187, 210, 222, 247, 260, 287, 301, 330, 345, 376, 392, 425, 442, 477,
495, 532, 551, 590, 610, 651, 672, 715, 737, 782, 805, 852, 876, 925, 950,
1001, 1027, 1080, 1107, 1162, 1190, 1247, 1276, 1335, … |
||
|
Illustration En haut ordinaires et en bas les supplémentaires |
|
Voir Produit infini de puissances de
2
|
|
||
|
Calcul des quantités de partitions par récurrence. |
On retrouve les nombres pentagonaux généralisés en exposant. Les exposants des paires de même signe sont séparés de 1, 2, 3, … Les exposants des paires de signes opposés sont séparés de 3, 5, 7, … Ce théorème est utilisé pour calculer rapidement la quantité Pn
de partitions
du nombre n. SUITE: calcul de la quantité
de partitions >>> |
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()