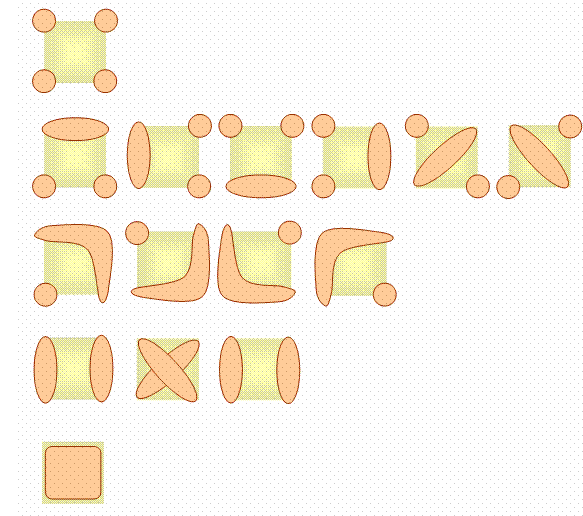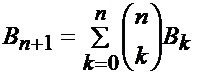NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 25/02/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Types de Nombres
Débutants Nombres	Dénombrement				Glossaire Nombres
INDEX Nombres FIGURÉS	Index par NOMS	Bell	Fibonacci	Pomerance
	Parts de tarte		Genocchi	Catalan
	Sommaire de cette page >>> Nombres de Bell >>> Liste >>> Polynômes de Bell

Nombres de Bell

Famille	Nombre / Dénombrement NOMBRES de BELL Nombres de Fibonacci
Approche	Prenons une tarte de trois parts. Combien de possibilités de la partager ? Seul je mange tout. À deux, avec un très bon ami, je lui concède deux parts, mais je me laisse le choix de celle qui reste pour moi. J'ai trois possibilités de découpe de la tarte. À trois, avec deux amis, chacun prend une part.

Définitions

Le nombre de Bell d'ordre n donne la quantité de partitions d'un ensemble de n éléments.

Exemples	B1 = 1	Un ensemble de "un" élément ne peut être découpé que d'une seule façon.
	B0 = 1	Un ensemble vide également (la seule partition de l'ensemble vide est l'ensemble vide).
	B2 = 2	{ , } { [ ] , [ ] }
	B3 = 5	{ A , B , C } { [ A , B ] , C } { A , [B , C ] } { [ A , C ] , B } { [ A ], [ B ], [ C ] }

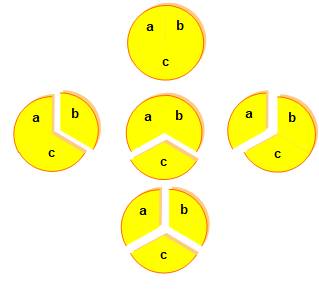
Construction

Exemple pour 4 Il y a 15 partitions (1 + 6 + 4 + 3 + 1).

Calcul

La formule pour calculer les nombres de Bell est bien compliquée !

Propriété

La réunion de chaque partition reforme l'ensemble complet En clair, c'est l'ensemble complet qui est découpé.

Anglais

Bell number Sequence of integers arising in combinatorics Bn is the number of partitions of a set of size n.

Liste des nombres de Bell Nombre de Bell et leur rang jusqu'à50

0, 1 1, 1 2, 2 3, 5 4, 15 5, 52 6, 203 7, 877 8, 4 140 9, 21 147 10, 115 975

DicoNombre Nb 1 Nb 2 Nb 5 15 52 203 877 4 140 21 147 115 975

11, 678 570 12, 4 213 597 13, 27 644 437 14, 190 899 322 15, 1 382 958 545 16, 10 480 142 147 17, 82 864 869 804 18, 682 076 806 159 19, 5 832 742 205 057 20, 51 724 158 235 372 21, 474 869 816 156 751 22, 4 506 715 738 447 323 23, 44 152 005 855 084 346 24, 445 958 869 294 805 289 25, 4 638 590 332 229 999 353 26, 49 631 246 523 618 756 274 27, 545 717 047 936 059 989 389 28, 6 160 539 404 599 934 652 455 29, 71 339 801 938 860 275 191 172 30, 846 749 014 511 809 332 450 147 31, 10 293 358 946 226 376 485 095 653 32, 128 064 670 049 908 713 818 925 644 33, 1 629 595 892 846 007 606 764 728 147 34, 21 195 039 388 640 360 462 388 656 799 35, 281 600 203 019 560 266 563 340 426 570 36, 3 819 714 729 894 818 339 975 525 681 317 37, 52 868 366 208 550 447 901 945 575 624 941 38, 746 289 892 095 625 330 523 099 540 639 146 39, 10 738 823 330 774 692 832 768 857 986 425 209 40, 157 450 588 391 204 931 289 324 344 702 531 067 41, 2 351 152 507 740 617 628 200 694 077 243 788 988 42, 35 742 549 198 872 617 291 353 508 656 626 642 567 43, 552 950 118 797 165 484 321 714 693 280 737 767 385 44, 8 701 963 427 387 055 089 023 600 531 855 797 148 876 45, 139 258 505 266 263 669 602 347 053 993 654 079 693 415 46, 2 265 418 219 334 494 002 928 484 444 705 392 276 158 355 47, 37 450 059 502 461 511 196 505 342 096 431 510 120 174 682 48, 628 919 796 303 118 415 420 210 454 071 849 537 746 015 761 49, 10 726 137 154 573 358 400 342 215 518 590 002 633 917 247 281 50, 185 724 268 771 078 270 438 257 767 181 908 917 499 221 852 770 Nombre de Bell premiers dans cette liste 2, 2 3, 5 7, 877 13, 27644437 42, 35742549198872617291353508656626642567

Polynômes de Bell
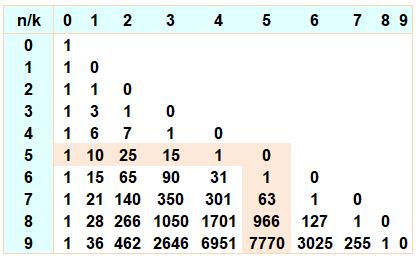
Polynôme qui généralise les nombres de Bell. Les coefficients forment le triangle de Stirling.	B0(x) = 1 B1(x) = x B2(x) = x^2 + x B3(x) = x^3 + 3x^2 + x B4(x) = x^4 + 6x^3 + 7x^2 + x B5(x) = x^5 + 10x^4 + 25x^3 + 15x^2 + x B6(x) = x^6 + 15x^5 + 65x^4 + 90x^3 + 31x^2 + x

Voir Triangle de Pascal / Triangle de Leibniz / Triangle de Narayana

Liens	Nombres de 1 à 100 et leurs diviseurs Nombre de Catalan
Sites	Nombres de Bell – Bibm@th Nombres de Bell – Wikipédia Nombres de Bell – Antonin Riffaut Bell Number – Wolfram MathWorld OEIS A000110 – Bell or exponential numbers: number of ways to partition a set of n labeled elements Bell Polynomial – Wolfram MathWorld OEIS A106800 – Triangle of Stirling numbers of 2nd kind, S(n, n-k), n >= 0, 0 <= k <= n
Cette page	http://villemin.gerard.free.fr/aNombre/TYPDENOM/Bell.htm