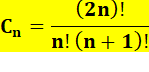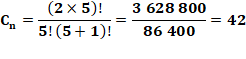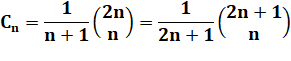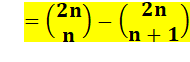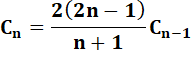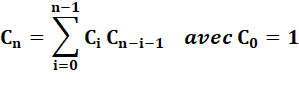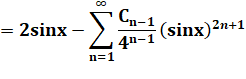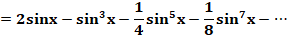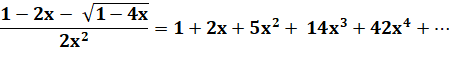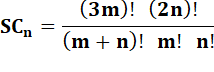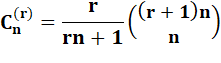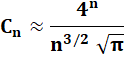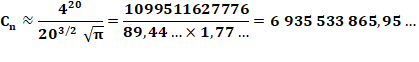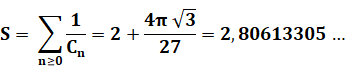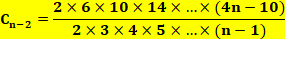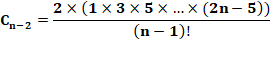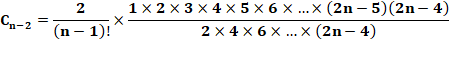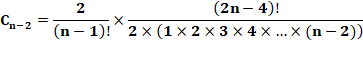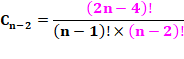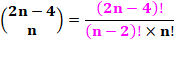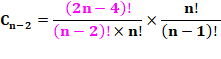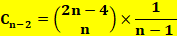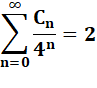Nombres de Catalan

Édition du: 04/04/2023

INDEX Graphe Logique Suites pour dénombrer Dénombrement Jeux et énigmes	Dénombrements - MOTIFS
	Nombres de Catalan		Nombres de Naryana		Nombres Manhattan
	*Nombres de Catalan – Développements*
	Définition	Pascal		Parenthèses		Polygones
	Valeurs	Hipparque		Escaliers		Illustrations
	Fuss-Catalan	Chemins de Dyck		Arbres

Faites un double-clic pour un retour en haut de page

Eugène Catalan

Nombres de Catalan

Constante de Catalan

Conjecture de Catalan

NOMBRES de CATALAN

Suite de nombres que l'on rencontre souvent pour compter des objets (combinatoire):

Combien peut-on dessiner de triangles dans un pentagone ?

Combien de possibilités d'arrangement des parenthèses ?

Combien de graphes différents ?

Etc.

Sommaire de cette page

>>> Nombres de Catalan en bref

>>> Triangle de Catalan – Construction

>>> Nombres de Catalan

>>> Propriétés des nombres de Catalan

>>> Applications typiques

Débutants

Dénombrement

Glossaire

Combinatoire

Anglais : Catalan Numbers

Nombres de Catalan en bref

Intérêt

Les nombres Catalan ont une place non négligeable et une importance majeure en combinatoire et en informatique.

Ils forment une séquence de nombres naturels qui se produisent dans l'étude d'un nombre étonnamment élevé de problèmes combinatoires. Ils apparaissent dans le problème de triangulation du polygone et du polyèdre, des arbres binaires, de l'ordre multiplicatif, du problème du chemin de réseaux, etc.

Aujourd'hui, l'application des nombres Catalan se voit en ingénierie dans le domaine de la géométrie algorithmique, des systèmes d'information géographique, de la géodésie, de la cryptographie et de la médecine.

En ce qui concerne les problèmes de géométrie algorithmique, ils sont généralement utilisés en modélisation géométrique. En cryptographie, ils sont utilisés dans la formation de clés pour le transfert sécurisé d'informations.

Bref historique

Alors qu'ils étaient connus des Chinois (1730), c'est Euler (1760) qui les redécouvre en comptant les triangles réalisés en traçant les diagonales non concourantes d'un polygone convexe.

Depuis, pratiquement tous les mathématiciens se sont intéressés aux nombres qui deviendront ceux de Catalan en 1948 après avoir été les nombres de Segner. Eugène Catalan (1838) étudie les combinaisons de lettres et de parenthèses et les associe aux nombres de Segner-Euler.

Aujourd'hui, on connait plusieurs centaines de cas d'applications des nombres de Catalan. Richard Stanley en publie 214 en 2015. La page consacrée aux nombres de Catalan est sans doute la plus importante de l'Encyclopédie des Entiers (OEIS A000108).

Voir Applications des nombres de Catalan / Historique des suites pour compter

Triangle de CATALAN		haut
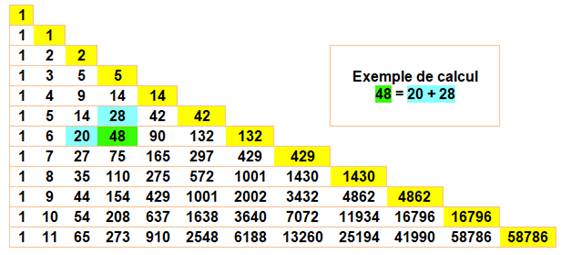
Construction Chaque nombre est la somme de ses deux voisins en haut et à gauche. Les nombres de Catalan sont en bout de ligne (jaunes).
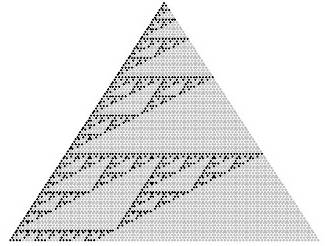
Triangle fractal Les nombres pairs du triangle sont remplacés par des "0" et les impairs par des "1". La figure prend une allure fractale comme pour la fractale de Sierpinski.	Source image: a Catalan number triangle fractal

Voir Nombres de Catalan et triangle de Pascal

Nombres de CATALAN

haut

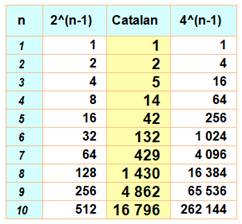
Valeurs

C₀ = 1*	C₁ = 1	C₂ = 2	C₃ = 5
C₄ = 14	C₅ = 42	C₆ = 132	C₇ = 429
C₈ = 1 430	C₉ = 4 862	C₁₀ = 16 796	…

* valeur parfois ignorée

Liste

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, 18367353072152, 69533550916004, … OEIS A000108

Note: la page OEIS sur les nombres de Catalan est surement la plus copieuse de cette encyclopédie. En 1976, R. Stanley a identifié 476 cas d'applications des nombres de Catalan.

Définition	Définition mathématique	Il existe une unique suite C_n (avec n≥0) d'entiers naturels satisfaisant aux deux conditions suivantes: C₀ = 1, et
Calculs	Formule de base (Catalan)
	Ex: le 5^e nombre de Catalan
	Avec coefficient du binôme
	Formule récurrente
	Une autre
	Angle double (Min An-Tu)
Série génératrice	Polynôme (Trouvé par Euler)
Généralisation	Super-Catalan
Nombres de	Fuss-Catalan	Utilisés pour la décomposition des polygones dont la triangulation pour r = 1 >>>

À l'infini	Tendance pour les grand n
	Ex: le 20^e nombre de Catalan	pour la valeur réelle: 6 564 120 420
Inverses	Leur somme
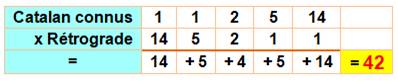
Calcul amusant !	Calcul récursif	Pour passer de 14 au suivant: 42
Attention	Nombres de Bell	Ne pas confondre avec les nombres de Catalan, alors que les deux suites sont voisines: Nombres de Bell: 1, 1, 2, 5, 15, 52, 203 … Nombres de Catalan: 1, 1, 2, 5, 14, 42, 132, 429, … Un nombre de Catalan est toujours inférieur que le nombre de Belle de même rang (rang > 4).

Voir Nombres de Dick

Formule originale de Catalan et formule d'Euler

Formule originale de Catalan

Or le coefficient du binôme:

Rapprochement:

Ce qui est la formule classique d'Euler

Voir Histoire des suites pour compter

Programme Maple – Nombres de Catalan

haut

But: lister les nombres de Catalan.

Commentaires: procédure Cat qui calcule le nombre de Catalan de rang n connaissant les précédents (voir formule).

Le programme principal demande de calculer la suite (seq) des nombres élaborés par la procédure.

L'option remember est très utile car elle permet de mémoriser les résultats au fur et à mesure de leurs calculs.

Voir Programmation – Index

Propriétés des nombres de Catalan		haut
Parité	Les nombres de Catalan sont tous pairs, sauf ceux en 2^k – 1.
Premier	Les seuls nombres de Catalan premiers sont: C₂ = 2 et C₃ = 5.
Encadrement
Somme	La convergence est extrêmement lente. Avec 30 termes, la valeur est seulement: 1,4495…
Marche aléatoire	Le marcheur part au point (0,0). À chaque pas, il monte (+1) ou il descend (–1). S'il atteint y = – 1, alors il y est bloqué. La quantité de chemins pour être bloqué après 2k+1 pas est le kième nombre de Catalan: C_k .
Chemins de Dyck	Chemins rectilignes en dessous de la diagonale sur une grille >>>

Voir Historique des suites pour compter

Applications – Exemples typiques		haut
Parenthèses	Quantité de n paires de parenthèses équilibrées. Pour n = 3, on a : C₃ = 5 ( ( ( ) ) ), ( ) ( ( ) ), ( ) ( ) ( ), ( ( ) ) ( ), ( ( ) ( ) )	>>>
Parenthèses et mots	Quantité de façons de placer n paires de parenthèses dans un mot de n + 1 lettres. Pour n = 3 on a: ( ( ab ) ( cd ) ), ( ( ( ab ) c ) d ), ( ( a ( bc ) ) d ), ( a ( ( bc ) d ) ), ( a ( b ( cd ) ) ).	>>>
Mots de Dyck	Quantité de mots de Dyck de longueur 2n Pour n = 3: XXXYYY, XYXXYY, XYXYXY, XXYYXY, XXYXYY	>>>
Escaliers Chemin de Dyck	Quantité de chemins en escalier contenus sous la diagonale d'une grille carrée. Chemin comportant 2n mouvements (cad. de longueur 2n).	>>>
Escalier – Pavage	Quantité de pavages de l'escalier avec n rectangles.	>>>
Marche	Quantité de chemin d'une marche aléatoire simple de longueur 2n + 1 avec arrêt en position y = – 1.
Arbres enracinés	Quantité d'arbres planaires enracinés (avec tronc) à n arêtes.	>>>
Arbres à nœuds	Quantité d'arbres binaires complets (sommets à 0 ou 2 descendants) comportant n + 1 feuilles (extrémités). Autrement-dit: arbres à n sommets (nœuds) internes.
Arbres divers	Quantité d'arbres pour diverses configurations d'arbres.	>>>
Triangulation des polygones	Quantité de façons de trianguler un polygone convexe de n + 2 côtés en dessinant des diagonales non sécantes.	>>>
Nombres	Nombres de n chiffres dont chacun progresse de 0 ou 1 et décroit de n'importe combien (comme 131 dans cet exemple). Pour n= 4, les quatorze possibilités: 1234, 1233, 1232, 1231, 1223, 1222, 1221, 1212, 1211, 1123, 1122, 1121, 1112, 1111.
Partitions	Quantité de partitions non-croisées.	>>>
Permutations	Quantité de permutations de (1, 2, …, n) qui ne contiennent pas un motif de trois nombres ordonnés.	>>>
Cordes et poignées de mains	Quantité de façons de disposer des cordes non sécantes dans le cercle.	>>>
Scrutin	Quantité de solutions au problème du vote de Bertrand	>>>

Suite en OEIS A000108

Suite	Arbres en général – Introduction, types Catalan et parenthèses Catalan et triangle de Pascal Historique des suites de nombres pour compter Nombres de Motzkin Nombres de Genocchi
Voir	Billard Coefficient du binôme Conjecture de Catalan Constante de Catalan Dénombrer – Index Eugène Catalan	Factorielle Méandres Nombres de Bell Premier Sous-factorielles
Livre	Time travel and other mathematical bewilderments – Martin Gardner – 1988 – pages 253 à 266: Catalan numbers
Sites	Nombres de Catalan – PJ Homière – Niveau universitaire OEIS A000108 – Catalan numbers: C(n) = binomial(2n,n)/(n+1) = (2n)!/(n!(n+1)!) Catalan Addendum – Richard P. Stanley – 2013 Catalan numbers – Richard P. Stanley – 2021 – Diaporama Catalan numbers – Robert Dikau – MC Tutor Catalan numbers and applications – Aybeyan Selimi, Muzafer SARAČEVIĆ History of Catalan numbers – Igor Pak (Voir Historique des suites pour dénombrer) Catalan Numbers – Richard P. Stanley – Diaporama de 113 vues Combinations of adding parentheses – code – La Vivien Post – Algorithme et programmation Java, Python, …
Cette page	http://villemin.gerard.free.fr/aNombre/TYPDENOM/Catalan/Catalan.htm