Nombres de Lucas-Carmichael

Édition du: 14/02/2020

INDEX Types de nombres	Types de Nombres – Diviseurs
	Parfaits	Semi-parfaits (SP)	SP Primitifs	SP Primaire
	Refactorisables	Pratiques	Abondant primitifs	Friables
	Facteurs-Diviseurs	Intouchables	Lucas-Carmichael	S-Parfait

NOMBRES de LUCAS-CARMICHAEL

Nombres en couples tels que tous les facteurs du premier plus un divisent le second, en l'occurrence le nombre suivant.

Sommaire de cette page

>>> Approche

>>> Définition

>>> Nombres de Lucas-Carmichael

>>> Programmation

>>> Nombre de Lucas-Carmichael avec écart k

Débutants

Nombres

Glossaire

Nombres

Approche		haut
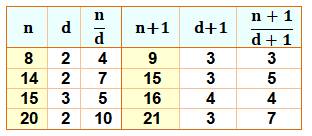
Divisibilité de n et de n + 1 Soit un nombre comme 8 = 2³, il est divisible par 2 et son successeur 9 = 3² est divisible par 3, nombre qui est le successeur de 2. Avec 9 = 3² et 10 = 2 x 5, aucun des facteurs de 10 n'est un successeur de 3. Le nombre 9 n'est pas éligible comme nombre L-C.
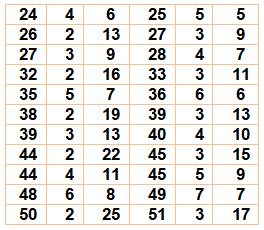
Trop nombreux ! En fait, de tels nombres sont nombreux. Leur étude ne présente pas un grand intérêt. Il faut réduire le périmètre de définition, notamment imposer que cette propriété de divisibilité s'applique à tous les diviseurs de n. Alors, le plus petit nombre éligible va devenir 399.

Voir Nombres facteurs-diviseurs comme introduction à cette page

Définition des nombres L-C		haut
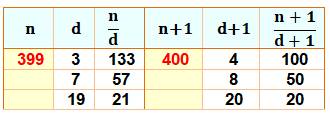
Définition Un nombre de Lucas-Carmichael est un nombre composé impair sans facteur carrés; et Tous ses facteurs premiers augmentés de 1 divisent n + 1.	Exemple Voir DicoNombre 399
Sans condition particulière le nombre 8, qui est un cube, serait un nombre L-C (tableau en haut). Ce serait le cas pour tous les cubes selon l'identité indiquée. C'est pourquoi, on exige que n soit sans facteur carré (tous les facteurs à la puissance 1).	n³ + 1 = (n + 1) (n² – n + 1) Le cube d'un nombre n, augmenté d'une unité, est divisible par n + 1. 8 + 1 = 2³ + 1 = 3 x (4 – 2 + 1) = 3 x 3

Nombres de Lucas-Carmichael		haut
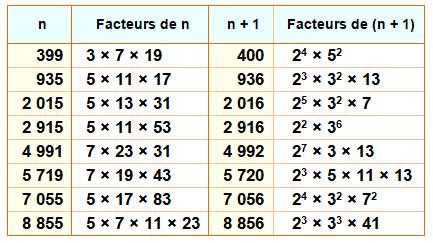
Lucas-Carmichael jusqu'à 10 000 Les huit premiers nombres L-C avec leurs facteurs. Pour 8 855, on vérifie que 8 856 est bien divisible par: 5 + 1 = 6 = 2 x 3, 7 + 1 = 8 = 2³, 11 + 1 = 12 = 2² x 3 et 23 + 1 = 24 = 2³ x 3
Liste	399, 935, 2015, 2915, 4991, 5719, 7055, 8855, 12719, 18095, 20705, 20999, 22847, 29315, 31535, 46079, 51359, 60059, 63503, 67199, 73535, 76751, 80189, 81719, 88559, 90287, 104663, 117215, 120581, 147455, 152279, 155819, 162687, 191807, 194327, 196559, 214199, …

Programmation Maple

haut

Commentaires

Programme qui recherche las nombres L-C et affiche les facteurs.

Procédure

La procédure SF indique si le nombre n est sans carré (T = 1), sinon il retourne T = 0. Valeur retournée également dans le cas des nombres premiers.

Le programme teste tous les exposants des facteurs F[i, 2] et place l'indicateur T à zéro si cet exposant est plus grand que 1.

Programme principal

Le programme principal explore les nombre impairs (by 2) et poursuit les traitements si SN(n) = 1, si le nombre n est composé sans facteur carré.

L'indicateur TT est mis à 1 en supposant que le nombre n est éligible. Il ne l'est plus dés qu'un diviseur d de n (ils sont dans la liste F) ne divise par n + 1. Alors l'indicateur est mis à 0.

Finalement, si TT a résisté à 1 en fin d'exploration des diviseurs, alors n est éligible comme L-C. On imprime ce nombre est son successeur avec leurs facteurs.

Résultat

En bleu, le résultat du traitement, lequel a été exploité pour réaliser le tableau ci-dessus.

Programme pour copie

restart: with(numtheory): SF := proc (n) local F, T, i; if isprime(n) then T := 0 else T := 1; F := ifactors(n)[2]; for i to nops(F) do if 1 < F[i, 2] then T := 0 end if end do end if; return T end proc; for n from 3 by 2 to 10001 do F := factorset(n); if SF(n) = 1 then TT := 1; for d in F do if `mod`(n+1, d+1) <> 0 then TT := 0 end if end do; if TT = 1 then print(n, ifactor(n), n+1, ifactor(n+1)) end if end if end do:

Voir Programme plus élaboré en OEIS A6972

Voir Programmation – Index

Nombre de Lucas-Carmichael avec écart k		haut
Lucas-Carmichael jusqu'à 1 000 pour k donné Un nombre k-L-C est un nombre L-C tel que les diviseurs de n, augmenté de k, divisent le nombre n + k En tête de ligne la valeur de k. Ainsi pour k = 2, une seule instance inférieure à 1000 avec 598. Alors: 598 + 2 = 600, divisible par: 2 + 2 = 4 13 + 2 = 15 = 3 x 5 23 + 2 = 25 = 5² Aucune instance avec k > 10. Notez que k = 6 et k = 8 sont absents.
Liste de la première instance pour k de 1 à 25	[1, 399], [2, 598], [3, 165], [4, 1886], [5, 715], [6, 148219], [7, 273], [8, 343027], [9, 231], [10, 935], [11, 3445], [13, 1547], [14, 2821], [15, 1105], [16, 21098], [17, 43183], [18, 258482], [19, 27071], [20, 2117473], [21, 3059], [22, 10373], [23, 2737], [24, 690501], [25, 1595]

Haut de page

Retour	Nombres intouchables
Suite	Facteurs-Diviseurs
Voir	Types de nombres
Livre	Ces nombres qui nous fascinent – J.-M. De Koninck – Ellipses, Paris 2008.
Sites	Nombre de Lucas-Carmichael – Wikipédia OEIS A6972 – Lucas-Carmichael numbers: squarefree composite numbers n such that p \| n => p+1 \| n+1
Cette page	http://villemin.gerard.free.fr/aNombre/TYPDIVIS/LucasCar.htm