|
Édition du: 20/08/2021 |
|
INDEX |
Types de Nombres – Diviseurs |
|||
|
Semi-parfaits (SP) |
||||
![]()
|
NOMBRES INTOUCHABLES Nombres qui ne
sont jamais la somme des diviseurs d'un nombre. Propriétés et liste de tels nombres.
Idem pour les nombres touchables qui sont somme des diviseurs de nombres et
parfois plusieurs fois. Records. |
||
|
|
Sommaire de cette page >>> Nombres intouchables >>> Observations – Remarques >>> Propriétés >>> Nombres touchables >>> Nombres hautement touchables >>> Liste des nombres – Accès aux tables >>> Programmation |
Débutants Glossaire |
Vocabulaire et notations
|
Un nombre n et ses diviseurs. La somme des diviseurs, y compris lui-même est
notée La somme des diviseurs, sans le nombre est notée |
|
Intouchables: film français Olivier Nakache et
Éric Toledano, sorti en 2011 avec François Cluzet et Omar Sy. Intouchables ou Dalits: nom d'une caste en Inde.
Individus considérés comme hors castes et affectés à des fonctions ou métiers
jugés impurs. |
Voir Nombre /
Division / Diviseurs
|
Approche |
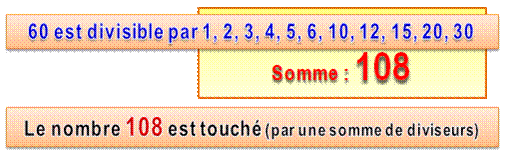
Le
nombre 108 est touchable, car il existe un nombre (60) dont la somme des
diviseurs stricts est égale à 108 (somme aliquote). |
|
|
Observations |
Voyons
la liste des sommes aliquotes
des nombres de 1 à 20: 0, 1, 3, 4, 6, 7, 8, 9, 10, 15, 16, 21, 22. Tous
ces nombres sont touchables par une somme
aliquote. Les
autres nombres: 2, 5, 11, 12, 13, 14, 17, 18, 19, 20 sont
des nombres intouchables, du moins pour
les sommes aliquotes des nombres de 1 à 20. |
|
|
Définitions |
Nombre
intouchable :
nombre qui n'est jamais la somme des diviseurs stricts
d'un nombre quelconque, y compris lui-même.
Il n'est jamais la somme aliquote
d'un nombre. Un nombre est intouchable s'il n'a
pas d'antécédent aliquote. Si l'on fait la liste de toutes les
sommes aliquotes, certains nombres ne sont pas présents dans cette liste; ce
sont les nombres intouchables par cette suite de nombres aliquotes. Nombre
sigma-intouchable :
nombre qui n'est jamais la somme des diviseurs (tous) d'un nombre quelconque,
y compris lui-même. |
|
|
Exemple |
Si on
considère le nombre 9. Diviseurs
propres: 1 et 3 (9 n'est pas un diviseur propre ou diviseur strict). Somme: 1 +
3 = 4 (on dit aussi: somme aliquote de 9) Conclusion:
4 est touchable, il est la somme aliquote
de 9.
Au
contraire, il est impossible de trouver une somme de diviseurs propres égale
à 5; ce nombre 5 est intouchable. |
|
|
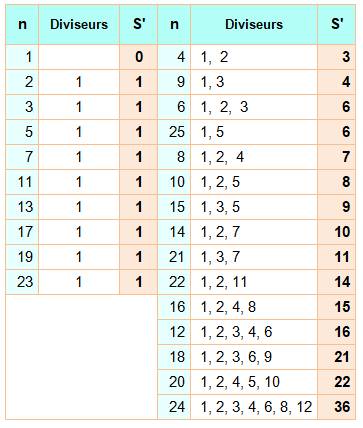
Nombres
de 1 à 25 Colonnes de gauche:
les nombres premiers dont le seul diviseur propre est 1. Colonnes de droites,
les autres nombres jusqu'à 25, ordonnés selon la valeur de la somme des
diviseurs propres. Ainsi, on note les nombres
manquants. Les nombres 2, 5, 12, 13, 17, 18, 19, 20, 23, 24 et 25 sont des intouchables sur la plage 1 à 25. |
|
|
|
Effet de
la plage d'exploration On cherche les nombres
intouchables jusqu'à 25 en analysant la somme des diviseurs propres jusqu'à
25, 100, 500 et 1000. Les
seuls vrais intouchables sont effectivement 2 et 5. Il faut atteindre n =
529 pour obtenir une somme de diviseurs propres égale à 24. |
I25/25 =
{2, 5, 12, 13, 17, 18, 19, 20, 23, 24, 25} I25/100 = {2, 5, 12, 18, 24} I25/500 = {2, 5, 24} I25/1000 = {2, 5} |
|
|
Infinité
– Prouvé par Erdös. Le
nombre 5 est le seul intouchable impair – Conjecture. Si tous les intouchables (> 5) sont pairs, alors la conjecture de
Goldbach indique qu'ils sont sommes de deux premiers: 2n = p + q Alors le produit
p.q a pour diviseurs propres: 1 , p et q La somme aliquote est 1 + p + q = 2n + 1 Et ce nombre, 2n + 1, n'est pas
intouchable. On sait que 1, 3 et 7 ne sont pas
intouchables (somme aliquote: 2, 4 et 8). Alors, seul 5 est intouchable
impair. |
s'(p)
= 1 s'(p²)
= 1 + p s'
(2p) = 1 + 2 + p = 3 + p
|
|
|
Soit une
somme aliquote comme 10, on cherche quel est le plus petit nombre dont la
somme des diviseurs strict est 14 ? C'est le
nombre n = 14. |
Diviseurs de 14 : 1, 2, 7, 14 Diviseurs stricts: 1, 2, 7 Somme aliquote: 1 + 2 + 7 = 10 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Quantité
de fois qu'un nombre est touché ? Nombres de 1 à 49 dans l'ordre
En vert,
le record de touches: une fois pour 3, deux fois pour 6, trois fois pour 31,
etc. Et, 9 592
fois pour 1, car il y a cette quantité de nombres premiers jusqu'à 100 000,
plage de la recherche. Enfin en
jaune, zéro fois pour les nombres intouchables 2 et 5. |
Nombres
hautement touchables Records
successifs de touches, hors nombres premiers: 0, 2 ; 1, 3 ; 2,
6
; 3, 21 ; 5,
31
; 6, 49 ; … Liste 2,
3, 6, 21, 31, 49, 73, 91,
115, 121, 169, 211, 301, 331, 361, 391, 421, 511, 631, 721, 781, 841, 1051,
1261, 1471, 1561, 1681, 1891, 2101, 2311, 2521, 2731, 3151, 3361, 3571, 3991,
4201, 4411, 4621, 5251, 5461, 6091, 6511, 6721, 6931, 7771, 7981, 8191, 9031,
… Détails ci-dessous |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Intouchables |
2, 5, 52, 88, 96, 120, 124, 146, 162, 188, 206, 210, 216, 238, 246, 248, 262,
268, 276, 288, 290, 292, 304, 306, 322, 324, 326, 336, 342, 372, 406, 408,
426, 430, 448, 472, 474, 498, 516, ... |
|
|
Touchables |
[s', n] => [3, 4], [4, 9], [6, 6], [7, 8], [8,
10], [9, 15], [10, 14], [11, 21], [12, 121], [13, 27], [14, 22], [15, 16],
[16, 12], [17, 39], [18, 289], [19, 65], [20, 34], [21, 18], [22, 20], [23,
57], [24, 529], [25, 95], … Exemple
de lecture: le nombre
s' = 6 est la somme des diviseurs stricts du nombre n = 6 (cas parfait)
et ce nombre n = 6 est le plus petit; le suivant avec s' = 6 serait 25. Avec s' =
8, on a n le plus petit égal à 10; le suivant serait 49. |
|
|
Hautement touchables |
2, 0, [ ] 3, 1, [4] 6, 2, [6,
25] Nombre
parfait 21,
3, [18, 51, 91] 31,
5, [32, 125, 161, 209, 221] 49,
6, [75, 215, 287, 407, 527, 551], 6 |
|
|
Sigma-intouchables |
2, 5, 9, 10,
11, 16, 17, 19, 21, 22, 23, 25, 26, 27, 29, 33, 34, 35, 37, 41, 43, 45, 46,
47, 49, 50, 51, 52, 53, 55, 58, 59, 61, 64, 65, 66, 67, 69, 70, 71, 73, 75,
76, 77, 79, 81, 82, 83, 85, 86, 87, 88, 89, 92, 94, 95, 97, 99, 100, … 1, 12, 24,
72, 168, 240, 336, 360, 504,
576, 720, 1440 |
|
|
Hautement sigma-touchables |
1, 12, 24,
72, 168, 240, 336, 360, 504, 576, 720, 1440, … |
Voir Suites aliquotes
|
Programme
|
But Établir la liste des nombres intouchables Explications Appel des logiciels de théorie des nombres. Initialisation de la liste L des sommes de
diviseurs propres. Lancement d'une boucle de calcul de ces sommes
pour les nombres de 1 à 2000. Somme en S et mémorisation de ces valeurs en L. Création de la liste M des nombres intouchables. Recherche pour chacun des nombres de 1 à 25 s'il
est présent dans la liste L des sommes de diviseurs. S'il n'est un membre de la liste alors ce nombre
est mémorisé dans la liste M. En fin de programme, impression de la liste M. En bleu résultat de l'exécution du programme. |
||
|
Programme avancé
Programme pour copie dans Maple |
Explications Création d'une suite (séquence)
conditionnelle: recherche des nombres touchés jusqu'à 101. Notez qu'il faut
chercher loin: ici, jusqu'à 10 000. Les accolades { }
convertissent la suite en un ensemble. Création d'un ensemble de nombre de 1 à 100. L'ensemble des nombres intouchables est la
différence entre ces deux listes. Notez que l'instruction minus n'agit que sur les ensembles. |
||
Voir Programmation – Index
|
Anglais |
||
|
Untouchable
numbers |
Not the sum of the proper divisors of any number. An untouchable number is a positive integer that
cannot be expressed as the sum of all the proper divisors of any positive integer
(including the untouchable number itself). That is, these numbers are not in
the image of the aliquot sum function – Wikipedia
. |
|
Voir
Anglais pour le bac et pour les affaires
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/TYPDIVIS/Intoucha.htm |