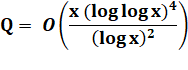NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 30/06/2017 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Types de Nombres
Débutants Général	FACTEURS			Glossaire Général
INDEX Types de nombres	Liste des types	Nombres de Zeisel	Paires de Ruth Aaron
	Sommaire de cette page >>> Définition >>> Liste des paires de Ruth-Aaron – Simples et pures >>> Paires puissantes >>> Triplets de Ruth-Aaron

Famille	Nombre / Division
Approche	Deux nombres consécutifs: 714 = 2 x 3 x 7 x 17 et 2 + 3 + 7 + 17 = 29 715 = 5 x 11 x 13 et 5 + 11 + 13 = 29 Sommes des facteurs égales.
Définitions	Paires de Ruth-Aaron Deux nombres consécutifs dont la somme des facteurs est identique. Ces deux nombres sont appelés nombres de Ruth-Aaron. S(n) = S(n + 1) Une infinité, sans doute. Triplets de Ruth-Aaron Trois nombres consécutifs dont la somme des facteurs est identique. S(n) = S(n + 1) = S(n + 2) Seuls sept triplets sont connus. Aucun quadruplet connu jusqu'à 10^10.
Catégories	Trois sortes de nombres selon les facteurs: N = X^k . Y^h Ssimple = X + Y avec k ou h >1 – Addition des facteurs uniques; Spur = X + Y avec k = h = 1 – Addition de facteurs uniques; Spuissant = kX + hT avec k ou h >1 - Addition de tous les facteurs, l'un au moins > 1.

Exemples

	N	N + 1	Sommes
Simple	24 = 2^3 x 3	25 = 5^2	2 + 3 = 5
Pur	5 = 5	6 = 2 x 3	5 = 2 + 3
Puissant	8 = 2^3	9 = 3^2	3 x 2 = 2 x 3 = 6

Origine

Nom donné par Carl Pomerance (Américain né en 1944) – Université de Georgie.

Babe Ruth et Hank Aaron sont des joueurs de baseball. Ruth déteint le record du nombre de coups avec 714 depuis 1935; record qui fut battu en 1974 par Aaron avec 715 coups (Il terminera sa carrière avec 755 homeruns).

Pomérance, aisi que son collègue David Penney, remarquent que le produit 714 x 715 = 510 510 est amusant et surtout, c'est le produit des sept premiers nombres premiers

714 x 715 = 510 510 = 2 x 3 x 5 x 7 x 11 x 13 x 17

Un étudiant de Pomerance, Jeremey Jordan, observe qu'en plus, la somme des facteurs premiers est égale pour les deux nombres.

714 = 2 x 3 x 7 x 17 et 2 + 3 + 7 + 17 = 29

715 = 5 x 11 x 13 et 5 + 11 + 13 = 29

Propriétés

Conjecture: il existe une infinité de paires de Ruth-Aaron. La démonstration d'Erdös a été infirmée. Nelson et al ont montré que la conjecture H e Schinzel impliquerait l'existence d'une infinité de paires de Ruth-Aaron.

Pomerance et Erdös ont prouvé en 1978, une conjecture de Nelson et al sur la répartition des paires de Ruth-Aaron. La somme des inverses des nombres de Ruth-Aaron tend vers 0,4207.

Source: Ruth-Aaron Pair de MathWorld

Formule

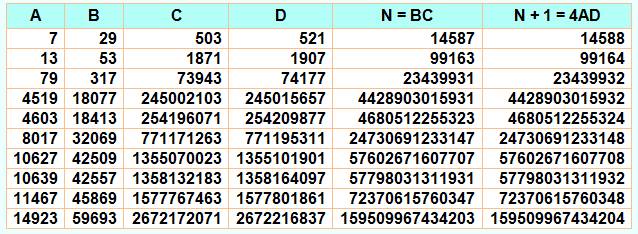
La formule suivante produit des nombres de Ruth-Aaron (pas tous, loin de là!)

A = 2n + 1	Si les quatre sont premiers, alors N = B.C N + 1 = 4 A.D forment une paire de Ruth-Aaron.
B = 8n + 5
C = 48n² + 24n – 1
D = 48n² + 30n – 1

Exemples

L'hypothèse H de Schinzel indique ces polynômes devraient être premiers une infinité de fois. Ce qui prouverait, si l'hypothèse était confirmée, que les paires de Rutj-Aaron seraient en nombre infini.

Densité

La densité des paires de Ruth-Aaron serait nulle (ils sont rares).

Pomerance et Erdös ont prouvé que:

Théorème

La quantité de nombres n x tels que S(n) = S(n+1) est:

Ce qui veut dire que la quantité Q est bornée.

Variantes

Paires à facteurs consécutifs Imposer que les facteurs premiers soient consécutifs Ex: 24 = 2 + 2 + 2 + 3 = 9 et 25 = 5 + 5 = 10 Il existe 55 telles paires jusqu'à 100 000. Sommes multiples Imposer que la somme des facteurs du premier égale k fois celle du suivant: S(n = k S(n+1).

Anglais

Ruth-Aaron pair A Ruth–Aaron pair consists of two consecutive integers (e.g. 714 and 715) for which the sums of the prime factors of each integer are equal. On April 8, 1974 when Hank Aaron surpassed the career home run record of 714 set by the immortal Babe Ruth by hitting his own 715th homer, mathematicians found yet another reason to cheer.

Liste des paires de Ruth-Aron – Simples et Pures

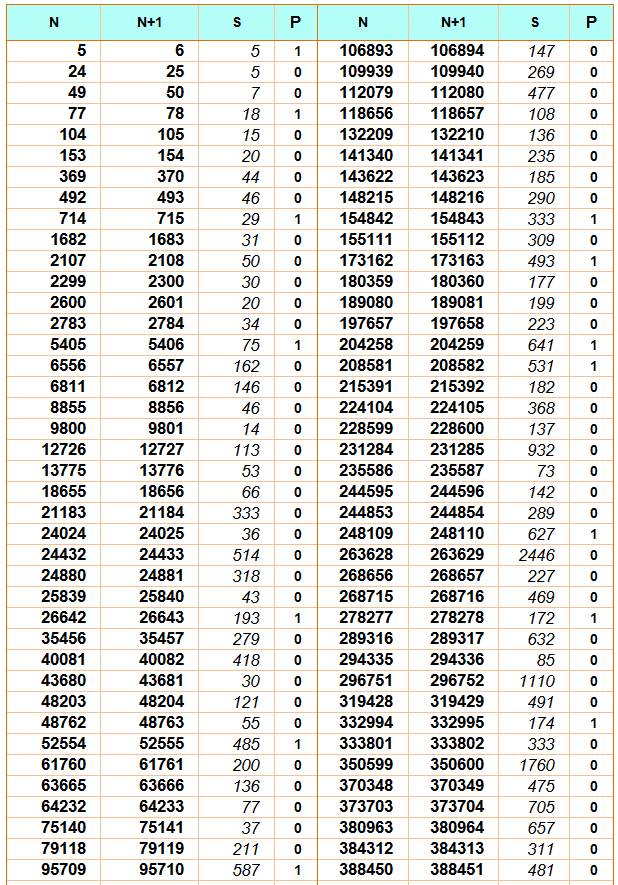
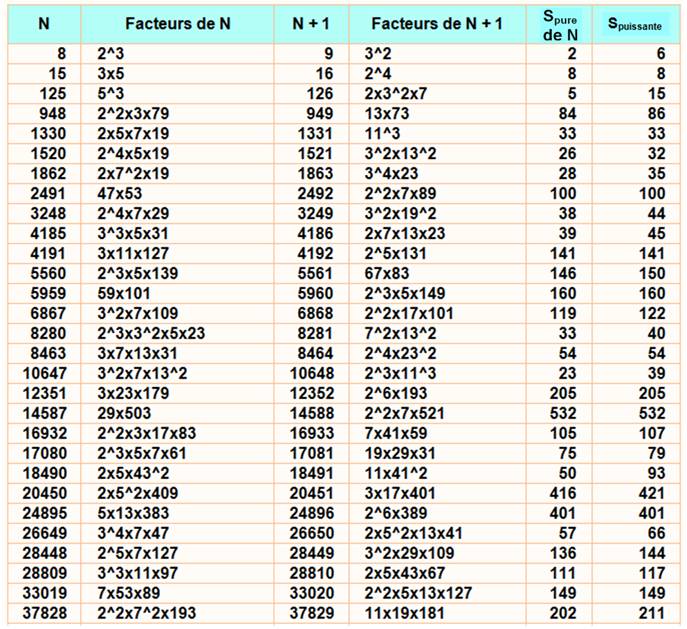
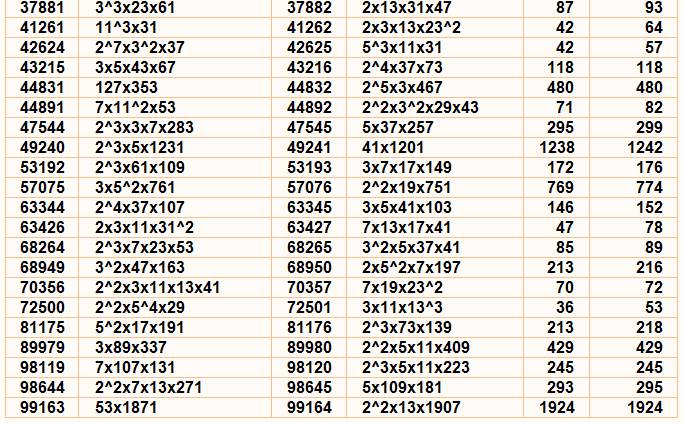
Paires avec indication des facteurs jusqu'à 10000

Paires de Ruth-Aaron simples et purs (en rouge)

N	Facteur de N	N + 1	Facteurs de N+ 1	Somme
5	5	6	2 x 3	5
24	2^3 x 3	25	5^2	5
49	7^2	50	2 x 5^2	7
77	7 x 11	78	2 x 3 x 13	18
104	2^3 x 13	105	3 x 5 x 7	15
153	3^2 x 17	154	2 x 7 x 11	20
369	3^2 x 41	370	2 x 5 x 37	44
492	2^2 x 3 x 41	493	17 x 29	46
714	2 x 3 x 7 x 17	715	5 x 11 x 13	29
1 682	2 x 29^2	1 683	3^2 x 11 x 17	31
2 107	7^2 x 43	2 108	2^2 x 17 x 31	50
2 299	11^2 x 19	2 300	2^2 x 5^2 x 23	30
2 600	2^3 x 5^2 x 13	2 601	3^2 x 17^2	20
2 783	11^2 x 23	2 784	2^5 x 3 x 29	34
5 405	5 x 23 x 47	5 406	2 x 3 x 17 x 53	75
6 556	2^2 x 11 x 149	6 557	79 x 83	162
6 811	7^2 x 139	6 812	2^2 x 13 x 131	146
8 855	5 x 7 x 11 x 23	8 856	2^3 x 3^3 x 41	46
9 800	2^3 x 5^2 x 7^2	9 801	3^4 x 11^2	14

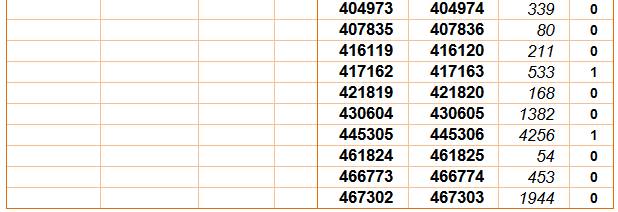
Paires simples jusqu'à 500 000

La colonne P est à 1 pour les paires pures

Liste des paires de Ruth-Aron – Puissantes
Paires puissantes jusqu'à 100 000 Notation: 2^3 = 2^3

Triplets de Ruth-Aaron
Triplets purs Seuls connus (Les trois derniers sont dus à Giovanni Resta)	89 460 294 = 2 × 3 × 7 × 11 × 23 × 8 419 89 460 295 = 5 × 4 201 × 4 259 89 460 296 = 2 × 2 × 2 × 31 × 43 × 8 389 et 2 + 3 + 7 + 11 + 23 + 8 419 = 5 + 4 201 + 4 259 = 2 + 31 + 43 + 8 389 = 8 465 151 165 960 539 = 3 × 11 × 11 × 83 × 2 081 × 2411 151 165 960 540 = 2 × 2 × 5 × 7 × 293 × 1 193 × 3 089 151 165 960 541 = 23 × 29 × 157 × 359 × 4 021 Somme = 4589 3 089 285 427 491 = 23 x 37 x 79 x 89 x 521 x 991 3 089 285 427 492 = 2^2 x 3^3 x 11 x 19 x 283 x 563 x 859 3 089 285 427 493 = 43 x 419 x 457 x 821 Somme = 1740 6 999 761 340 223 = 109 x 1693 x 10 487 x 3 617 6 999 761 340 224 = 2^6 x 17 x 241 x 1 949 x13 697 6 999 761 340 225 = 3^2 x 5^2 x 23^2 x 37 x 101 x 15 737 Somme = 15 906 7 539 504 384 825 = 3^2 × 5^2 × 7^2 × 43 × 251 × 63 361 7 539 504 384 826 = 2 × 19 × 367 × 10 181 × 53 101 7 539 504 384 827 = 17 × 457 × 26 309 × 36 887 Somme = 63 670
Triplets puissants Seuls connus jusqu'à 10^13	417 162 = 2 × 3 × 251 × 277 417 163 = 17 × 53 × 463 417 164 = 2 × 2 × 11 × 19 × 499 et 2 + 3 + 251 + 277 = 17 + 53 + 463 = 2 + 2 + 11 + 19 + 499 = 533 6 913 943 284 = 2 × 2 × 37 × 89 × 101 × 5 197 6 913 943 285 = 5 × 283 × 1 259 × 3 881 6 913 943 286 = 2 × 3 × 167 × 2 549 × 2 707 et 2 + 2 + 37 + 89 + 101 + 5197 = 5 + 283 + 1259 + 3881 = 2 + 3 + 167 + 2549 + 2707 = 5428

Suite	Liste des types de nombres selon leurs facteurs Nombres dont le plus grand facteur est égal à la somme de leurs chiffres.
DicoNombre	Nombre 714 Nombre 510 510
Site	Puzzle 173. Ruth-Aaron Triplets Ruth-Aaron Numbers revisited – C. Pomerance – Niveau avancé. OEIS A006145 OEIS A039752 OEIS A227654 Ruth-Aaron pairs – Numbers aplenty
Cette page	http://villemin.gerard.free.fr/aNombre/TYPDIVIS/RuthAaro.htm