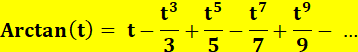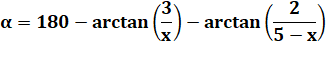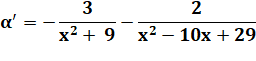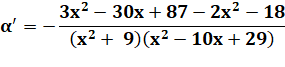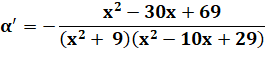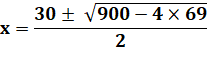NOMBRES – Curiosités, Théorie et Usages

 

Accueil                           DicoNombre            Rubriques           Nouveautés      Édition du: 13/11/2021

Orientation générale        DicoMot Math          Atlas                   Actualités                       M'écrire

Barre de recherche          DicoCulture              Index alphabétique        Références      Brèves de Maths

        

Trigonométrie

 

Débutants

Pente

CALCULS AVANCÉS

 

Glossaire

Opérations

 

 

INDEX

 

Calculs

 

Trigonométrie

Arctan

Cosécante

Congruence avec trigonométrie

Réciproques – arcsin, arccos, arctan

 

Sommaire de cette page

>>> Approche

>>> Tangente & arc tangente

>>> Formule de Grégory

>>> Cas de l'angle de 45°

 

>>> Calcul de Pi

>>> Formule de Machin

>>> Formule d'Euler

>>> Arctan & Fibonacci

>>> Arctan et dérivation

 

 

 

 

ARC TANGENTE d'un nombre

 

Où il est question de pentes, de Fibonacci et de Pi.

 

L’arc tangente d'un nombre réel  est la mesure d'un angle orienté dont la tangente vaut ce nombre.

 

 

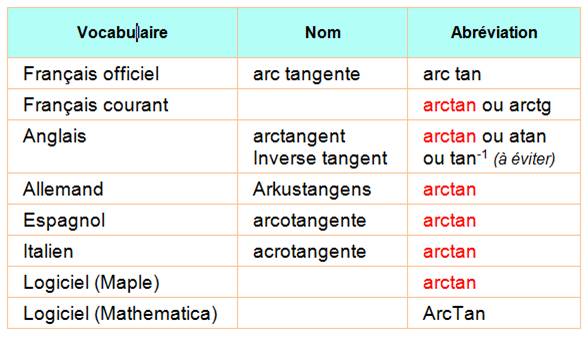
Arc tangente selon les pays

 

 

APPROCHE

 

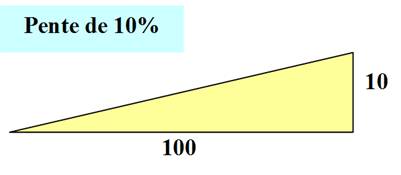
Pente

*      On mesure la pente d'une route en donnant un pourcentage.

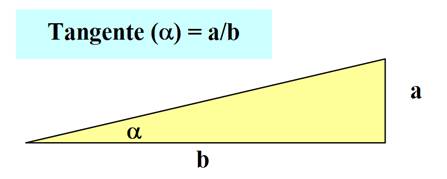
Combien de mètres de montée pour 100 mètres de route.

La pente ainsi définie est appelée tangente de l'angle

Voir Pourcentage

 

 

*      Tangente (angle) = 10/100             =>      angle    = 5,7°

Pente                   de 10%                 =>      angle de 5,7°

 

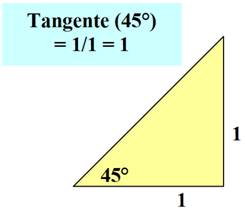
*      Parfois, on donne la hauteur par rapport à la distance parcourue sur la route.

Ce n'est pas le cas en mathématiques.

Voyons, à titre d'exemple, une même montée:

 

Classique

Attention

Montée de 100 m

Sur une distance horizontale de 100 m

Sur une route de 100 m

=> Route à 45°

=> Route verticale

& Pente = 1 (100%)

& Pente infinie

 

 

 

 

 

 

 

 

TANGENTE & ARC TANGENTE

 

La fonction inverse

 

Les deux notations suivantes sont équivalentes

 

Tangente () = a / b = t

Arctan (t) =

Avec le ratio

On calcule l'angle

Avec l'angle

On calcule le ratio

Tangente (45°) = 1 / 1 = 1

Arctan (1) = 45°

 

 

 

 

FORMULE DE GRÉGORY

 

 

Formule de Gregory (1638-1675)

 

 

 

*      La série converge si t est inférieur ou égal à 1; alors chacun des termes devient de plus en plus petit.

*      Justement dans le cas où   = 45°, alors  t = 1, et:

45° = Arctan (1) = 1 – 1/3 + 1/5 – 1/7 + 1/9 – …

 

 

 

Mesure des angles

On mesure classiquement les angles en degrés

1 tour complet = 360°

On peut aussi donner la longueur de l'arc

1 tour complet = 2  R

En général on simplifie en prenant le cercle de rayon unité

1 tour complet = 2

On a créé une nouvelle unité

1 tour complet = 2  radians

 

On déduit les égalités suivantes

Radians

Degrés

2

= 360

= 180

 / 2

= 90

 / 4

= 45

 

 

 

 

CAS DE L'ANGLE DE 45°

 

Magie de la formule de Grégory

 

*      Reprenons la formule ci-dessus

45° =  / 4 = Arctan (1) = 1 – 1/3 +1/5 – 1/7 + 1/9 – …

 

 

*      C'est Gottfried Leibnitz (1646-1716) qui a trouvé cette valeur à partir de la formule de Grégory

 

Un filon de formules

 

*      À condition que t soit inférieur à 1, on peut calculer toutes les formules que l'on veut

*      Voyons avec 30° =  / 6

Tangente (30°) = 1 / 3

Arctan (1 / 3) =  / 6

*      Et avec la formule:

 / 6 = 1/3 - 1/(3 x 33) + 1/(5 x 93) - …

*      Avec 1/3 en facteur:

 / 6 = (1/3) ( 1 - 1/(3 x 3) + 1/(5 x 9) - …

*      Soit la nouvelle formule pour

 

 

 

 

 

CALCUL DE PI

 

Calcul de  avec ces formules

 

*      En fait, la formule initiale converge très lentement.

Pour 6 décimales, il faut calculer 5 millions de termes.

La seconde formule produit 6 décimales avec 10 termes calculés.

Mais, inconvénient, il faut être capable de calculer la racine de 3.

*      Par contre les premiers termes sont esthétiques!

 

 

 

Termes de la formule en

1

 

1

1/3

–

0,333333333333333333

1/5

+

0,2

1/7

–

0,142857142857142857

1/9

+

0,111111111111111111

1/11

–

0,090909090909090909

1/13

+

0,076923076923076923

Somme algébrique

36 979 / 45 045

=

0,820934620934620934

 

x 4 =>

3,28373848

Et…

3,14

 

 

Termes de la formule en

1

 

1

1/9

–

0,111111111111

1/45

+

0,022222222222

1/189

–

0,005291005291

1/729

+

0,001371742112

1/2673

–

0,000374111485

1/9477

+

0,000105518624

Somme algébrique

3 309 041 / 3 648 645

=

0,9069232550714032195

 

x 23   =>

3,1416743126988376716

Et…

3,1415926535897932385

 

 

 

 

 

 

FORMULE DE MACHIN

 

 

Combinaisons

Formule de Machin (1680-1752)

 

 / 4 = 4 arctan (1/5) – arctan (1/239)

 

Calcul

1/5

 

0,200000000000000

1/375

–

0,002666666666666

1/15625

+

0,000064000000000

1/546875

–

0,000001828571428

1/17578125

+

0,000000056888889

1/537109375

–

0,000000001861818

1/15869140625

+

0,000000000063015

1/457763671875

–

0,000000000002184

1/12969970703125

+

0,000000000000077

1/362396240234375

–

0,000000000000002

Total A = arctan (1/5)

=

0,197395559849880

 

1/239

+

0,004184100418410

1/40955757

–

0,000000024416591

Total B = arctan (1/239)

=

0,004184076002074

 

A = arctan (1/5)

=

0,197395559849880

B = arctan (1/239)

=

0,004184076002074

= 16A – 4B

=

3,141592653589792

Et… 

=

3,1415926535897932385

 

 

 

 

 

FORMULE D'EULER

 

 

Formule d'Euler (1707-1783)

 

 / 4 = arctan (1/2)  + arctan (1/3)

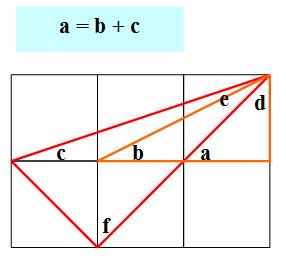
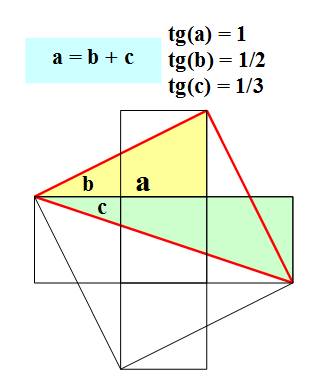
arctan(1/1) = arctan (1/2)  + arctan (1/3)

 

Interprétation géométrique (les lettres représentent des angles)

 

 

 

Calcul

Somme des angles = 180° dans un triangle rectangle

a + d + 90 = 180

c + (e + d) + 90 = 180

f = 2 x 45°est bien un angle droit

tg (b) = 1/2

tg (e) = 1/2

b = e

En remplaçant dans la formule du haut

c + e + d = 90

c + b + d = 90

c + b + (90 – a) = 90

a = c + b

 

Conclusion

tan ( a )

= 1 / 1

tan ( b )

= 1 / 2

tan ( c )

= 1 / 3

a = c + b  =>

arctan(1/1)

= artg(1/2) + arctan(1/3)

 

Autre illustration astucieuse

 

 

 

 

 

PI calculé par arctan – Remarques

 

*       Pour calculer  avec beaucoup de décimales une bonne méthode consiste à utiliser l'arc tangente. Notez que: interroger un ordinateur en utilisant ses propres fonctions arctan n'est pas la solution pour obtenir des milliers de décimales, sauf si le calcul utilise explicitement les techniques qui sont développées ci-dessous.

*       Le développement en série de arctg est :

  

Pour x < 1, cette série converge; et

Pour x = 1 elle converge aussi mais très lentement vers arctg 1 =  /4.

  

*       Dans la mesure où chaque terme suivant de la série est réduit par x², il est intéressant de prendre x très petit. On prendra pour x, l'opposé d'un nombre entier pour faciliter les calculs.

 

Voir Liste de formule en arctan pour calculer Pi

 

 

ARCTAN & FIBONACCI

 

Généralisation

Introduction des Fibonacci

 

 =

arctan(1)

=

arctan(1/2) + arctan(1/3)

=

arctan(1/2) + arctan(1/5) + arctan(1/8)

=

arctan(1/2) + arctan(1/5) + arctan(1/13) + arctan(1/21)

=

arctan(1/2) + arctan(1/5) + arctan(1/13) + arctan(1/34) + arctan(1/55)

 

Etc.

 

*      On note que chaque dénominateur et la somme de deux dénominateurs précédents (selon deux motifs de calcul):

5 = 3 + 2

13 = 8 + 5

21 = 8 + 13

 

 

Arctan et dérivation

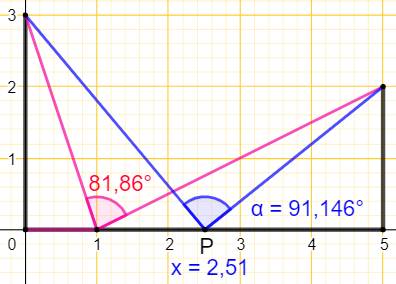
Construction

Une forme en U avec base de 5 cm et deux bords de 3 et 2 cm.

Comment placer le point P sur la base pour obtenir le plus grand angle alpha ?

 

En rose, position quelconque.

En bleu, position avec angle alpha maximum, assez proche du point milieu. Ce serait le milieu si les bords étaient de même taille.

Valeur de l'angle

Dérivée

 

Voir Dérivées  Formulaire 

 

Angle maximum pour  selon hauteur y d'un des bords

 

Dérivée nulle

Valeur dans l'intervalle

 

 

 

 

 

Suite en 

*    Pente - Débutant

*    Calcul de Pi avec les Arctan

*    Tangente

Voir

*    Multiplications védiques

*    Calcul des carrés

*    Calcul mental

*    Théorie des nombres

*    Calcul de Pi avec les Arctan

*    Fibonacci

Sites

*    Fibonacci Numbers and the Golden Section

Cette page

http://villemin.gerard.free.fr/Calcul/Arctg.htm