|
||||||||||||
|
PIONS
BLANCS et NOIRS Possibilité pour un pion d'une couleur
de se retrouver toujours voisins d'un pion de même couleur. |
|
|
|
|
Situation de proximité
Exemple
Note: marron adjectif
est invariable |
|
|
|
||
|
Un pion
|
0 +
1 = 1 |
|
|
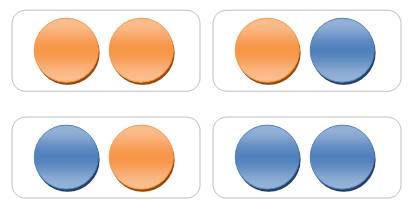
Deux pions
|
1 + 0 + 0 + 1 = 2 |
|
|
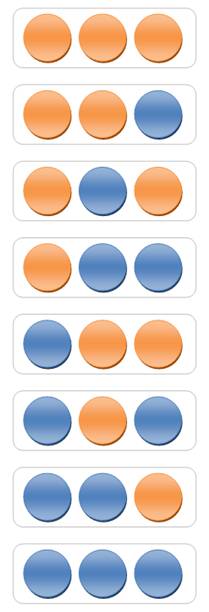
Trois pions
000 001 010 011 100 101 110 111
|
1 + 1 + 0 + 0 + 1 + 0 + 0 + 1 = 4 |
|
Quatre pions
|
0000 0001 0010 0011 0100 0101 0110 0111 =>3 cas Note: le 100
était valide; mais avec le 0 en tête, 0100 n'est plus valide car le 0 en tête
est seul, sans 0 voisin. |
1000 1001 1010 1011 1100 1101 1110 1111 =>4 cas Note: le 100
était valide et, il le reste avec l'ajout du 1 en tête. |
|
Cinq pions
|
00000 00001 00010 00011 00100 00101 00110 00111 =>5 cas |
01000 01001 01010 01011 01100 01101 01110 01111 =>0 cas |
10000 10001 10010 10011 10100 10101 10110 10111 =>3 cas |
11000 11001 11010 11011 11100 11101 11110 11111 =>3 cas |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Décompte selon n pions
Généralisation P(n) = 2P(n–1) – P(n – 2) + P(n – 3) P(n+1) / P(n) = 1,754877666247... Ratio = 1,754 877 666 24... = Racine de
x3 – 2x2 + x – 1 = 0 Trois voisins
Ratio = 1,618 … et 0, 618 = nombre d'or et son inverse Racines de x4 – 2x3 + x2
– 1 = (x² - x – 1)(x² - x + 1) = 0 0, 5 + i x 0,8660254040
et 0, 5 – i x 0,8660254040. Quatre voisins Ratio = 1,528946355 … Racine de x5 – 2x4 + x3
– 1 Plus quatre racines complexes 0,7362751327
+ i x 0,8216467855 0,7362751327
– i x 0,8216467855 - 0,5007483100 + i x 0,5353363226 - 0,5007483100
– i x 0,5353363226 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
D'après The book of numbers – Conway et Guy – Copernicus – 1996 – page 205
|
Suite |
|
|
Voir |
|
![]()