|
Édition du: 09/03/2024 |
|
INDEX |
QUADRILATÈRES – Compter |
||
|
|
|||
![]()
|
Quantité de triangles rectangles
Une grille régulière (m, n). Combien de triangles
rectangles de dimension (p, q) ? Dénombrement utile pour compter la quantité de
droites passant par k points dans une grille. |
||
|
|
Sommaire de cette page >>>
Approche: triangle (2, 1) et grille (4, 4) >>>
Cas: triangle (2, 1) et grille (5, 4) >>>
Cas:
triangle (2, 1) et grille (6, 5) >>>
Cas: triangle (3, 1) et grille (7, 5) >>> Quantité de lignes par 2 points – Grille (4, 4) |
Débutants Glossaire |
Triangles équilatéraux, hexagones, carrés
|
Il est impossible de dessiner un triangle
équilatéral comme un hexagone sur les sommets d'une grille >>> Les carrés entiers sur une grille ont pour côtés
la suite des nombres sommes de deux carrés >>> |
|
|
||
|
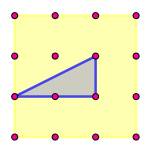
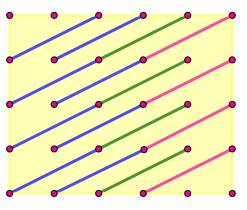
Une
grille (m, n) = (4, 4) et un triangle rectangle dont les côtés mesurent (p,
q) = (2, 1). On ne
dessine que l'hypoténuse pour la clarté de la représentation. Ici on
dénombre 6 segments bleus. Avec les rotations, il y en a 4 fois plus. La
quantité de triangles rectangles de base (de segments bleus) est égal à: Note: m et q pour l'horizontale et n et p pour la
verticale. |
|
|
|
|
||
|
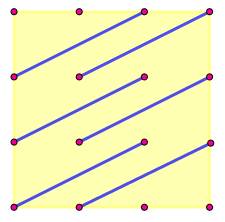
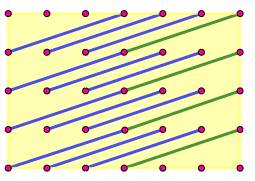
Grille
précédente prolongée, créant trois triangles rectangles supplémentaires: 3
segments verts dont 2 dans le prolongement de traits bleus existants. La
quantité de segments dans le
prolongement est égal à: Soit la
quantité de droites obliques: |
|
|
|
|
||
|
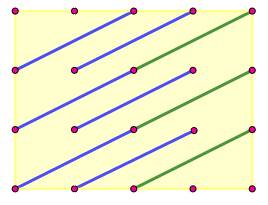
Q(6521) = (6 – 2) (5 – 1) = 4 x 4 = 16 P(6521) = (6 – 2x2) (5 – 2x1) = 2 x 3 = 6 O(6521) = 16 – 6 = 10 La quantité de droites passant par 2 points (ou plus)
selon une oblique (2, 1) est 4 x 10 = 40. |
|
|
|
|
||
|
Q(7531) = (7 – 3) (5 – 1) = 4 x 4 = 16 P(7531) = (7 – 2x3) (5 – 2x1) = 1 x 3 = 3 O(7531) = 16 – 3 = 13 |
|
|
|
|
|||
|
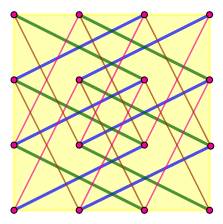
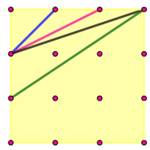
Sur cette
grille, on peut former quatre types de triangles rectangles dont a visualisé
l'hypoténuse. |
|
||
|
Bleu Q(4411) = (4 – 1) (4 – 1) = 3 x 3 = 9 P(4411) = (4 – 2x1) (4 – 2x2) = 2 x 2 = 4 O(4411) = 9 – 4 = 5 Total: 2 x 5 = 10 avec obliques dans l'autre
sens. VOIR Suite du calcul pour les autres cas. |
|
||
|
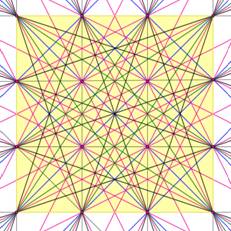
Bilan grille 4 x4 Avec les 2x4 droites horizontales et verticales: 8 + 10 + 24 + 12 + 8 = 62 Sur une grille 4x4, on peut tracer 62 droites qui
passent par deux points ou plus. |
|
||
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()