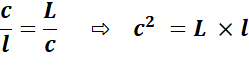|
|||||||||||||||||||||||||||||||||||||
![]()
Humour
|
Peut-on c |
Voir J-L Fournier
/ Expression
avec le mot "carré"
Énigme
|
|
Voir Solution
|
CARRÉ ou TÉTRAGONE Un carré est un parallélogramme.
Un carré est:
Mesures principales:
Le carré possède:
|
Voir Nombres
carrés / Aire du carré et de la couronne carrée
/ Square
|
|
||
|
Quatre angles droits
Voir Nombre
360 |
|
|
|
|
||
|
Symétrie
|
|
|
|
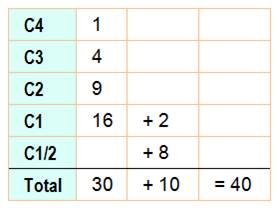
Bilan
|
|
|
Voir
Racine de 2 / Doubler
le volume du cube / La ville
idéale de Platon / Jeux divers
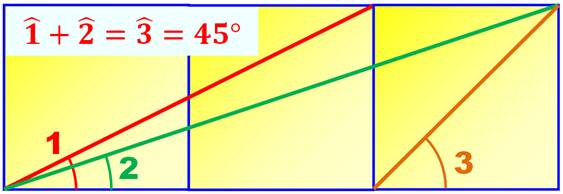
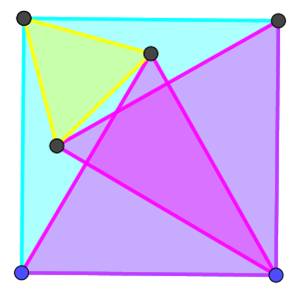
Propriété amusante avec trois carrés identiques

Angle 1 = 26,56° et angle 2 = 18,44°
Voir Démonstration / Brève 54-1077
|
Une
piscine flanquée de quatre arbres aux
coins. La
famille grandit et le propriétaire souhaite doubler la surface de la piscine. S'il
est prêt à refaire le dallage, il ne veut pas sacrifier ses arbres. Comment
s'y prendre? |
|
|
DOUBLER LE CARRÉ |
|
|
|
Problème
Tentative
1
Tentative
2
Solution
Solution
imaginée par Platon ( 428 - 348 av. J.-C.) dans son dialogue sur la vertu |
|
|
|
Deuxième
solution
appliqué ici, donne: c² = a² + a² = 2a².
|
|
|
|
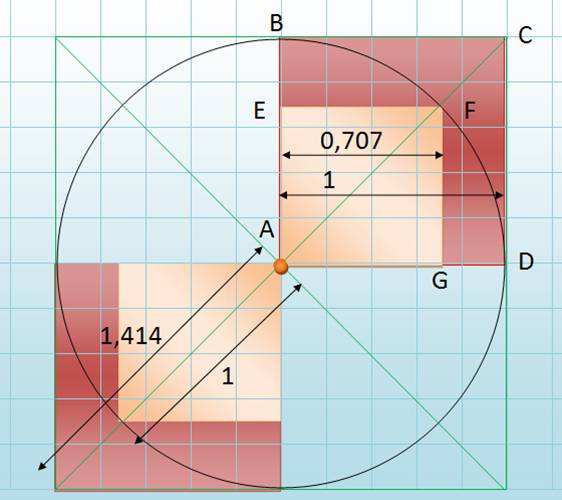
Les
arbres sont conservés en tournant la piscine de 45° La
surface sera doublée en agrandissant chacun des côté par un facteur égal à
racine de 2 = 1,414… |
|
|
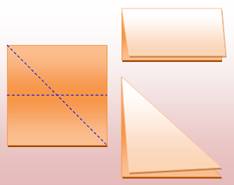
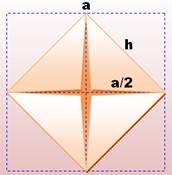
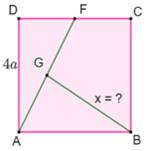
Question Un carré est plié
exactement en deux
et son périmètre est
12 cm. Quelle est la longueur
du côté du carré originel?
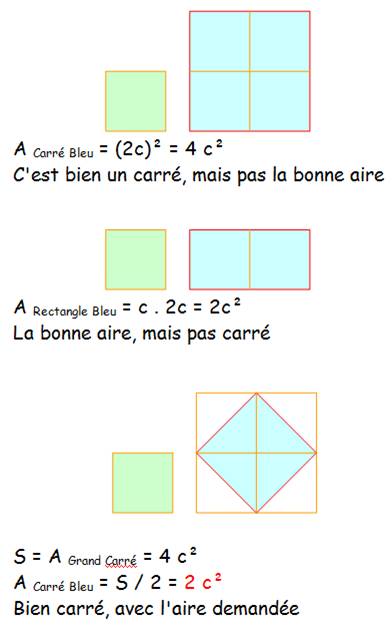
1) Plié en rectangle, par une médiane:
2) Plié en triangle par une diagonale: Avec le théorème
de Pythagore
Aire du grand
carré = 2 fois celle du petit (cf. rubrique précédente) comme il est demandé dans l'énoncé. |
Voir Énigmes
– Index
Merci à J-P M. pour ses remarques
|
|
||
|
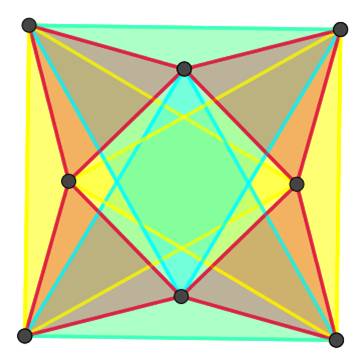
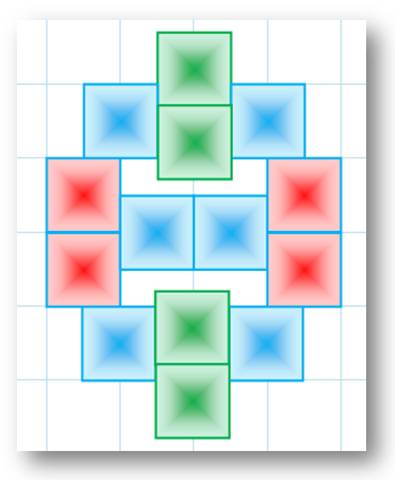
Figure formées en traçant les quatre
triangles équilatéraux sur les côtés du carré. Les quatre sommets des triangles forment un
nouveau carré sur lequel on dessine les triangles équilatéraux extérieurs.
Les nouveaux sommet sont les sommets du carré initial. Remarquez l'octogone central. Il n'est pas
régulier. Ses angles sont alternativement 120° et 150°. |
|
|
Voir Octogone
|
|
|
|
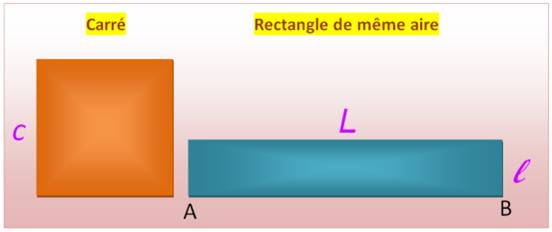
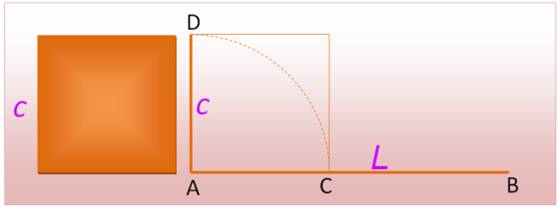
Périmètre
et aire Lorsque deux
champs, un carré et l'autre rectangulaire, ont le même périmètre, celui qui
couvre la plus grande surface est le champ carré. Voir Somme et produit Transformation
Départ
avec AB = L
Comment trouver la
largeur l connaissant la
longueur L? Préparation avec
AC = AD = c
Construction avec EC // DB
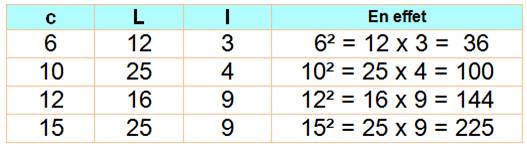
Aire carré = Aire rectangle Exemples
|
|
|
Quel
sont les deux seuls drapeaux nationaux carrés
dans le monde? |
|
|
|
|
|
|
Moucharabié à base de carrés, observé à Djerba - Tunisie
|
|
|
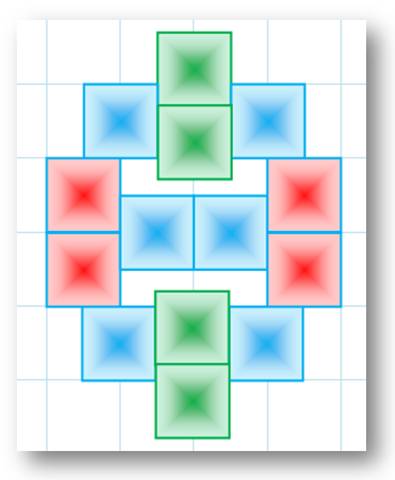
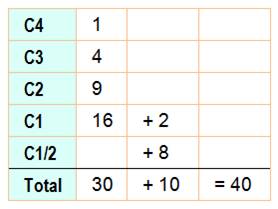
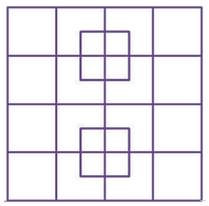
Le
maximum possible est 14
carrés accolés, chacun en touchant trois autres. Aucune solution avec chacun
en touchant quatre. |
Voir Jeux
et énigmes / Problème des quatre couleurs
|
Les
deux seuls carrés du monde: Vatican et
Suisse. Le
drapeau de la Croix-Rouge, inverse de celui de la Suisse, est rectangulaire.
|
Retour / Géographie /
Vatican / Croix
![]()
|
|
|
|
Carré: du
latin quadratus, devenu quarré ou carrez. Carré d'agneau:
le carré est un morceau de viande d'agneau, de mouton ou de porc rassemblant
l'ensemble des côtes découvertes, secondes et premières. Carré du
cimetière: il regroupe des défunts de même confession. Carré d'as: quatre
as dans un jeu de cartes. Ou autres cartes. Carré des
officiers: pièce commune sur un navire, donnant accès
aux cabines des officiers. Carré Hermès:
foulard en twill de soie de 90 cm x 90 cm. Nom officiel donné en 1960. Son
coût dépasse les 360 euros. Voiles carrées:
voile de bateau carrée, traversée verticalement par le mât qui la porte. |
Autre
acceptions sur le Wiktionnaire / Voir DicoMot
![]()
![]()