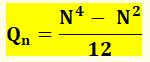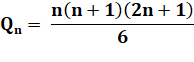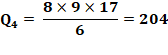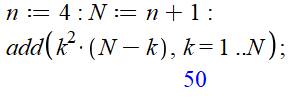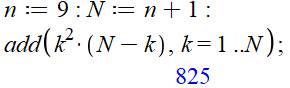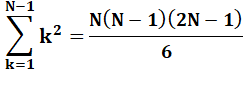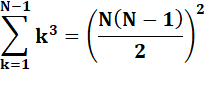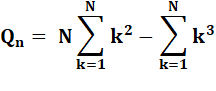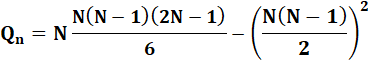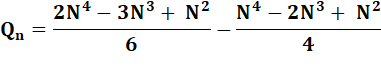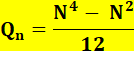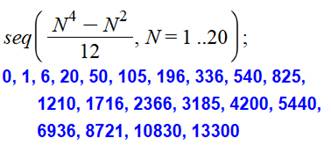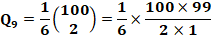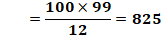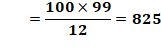|
Édition du: 28/12/2024 |
|
INDEX |
QUADRILATÈRES – Compter |
||
|
|
|||
Faites
un double-clic pour un retour en haut de
page
![]()
|
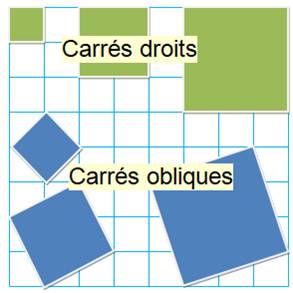
Quantité de CARRÉS droits ou obliques dans le quadrillage d'un carré
La
formule, pour N points par côté, est celle
indiquée. Sur les pages précédentes:
|
||
|
|
Sommaire de cette page >>> Types: droits ou
obliques >>> Carrés droits >>> Carrés obliques >>> Calcul de la formule |
Débutants Glossaire |
|
Problème Soit
une grille de dimension finie n × n. n
est la quantité de cellules sur un côté. N
est celle des points sur un côté N = n + 1 Quels
sont tous les carrés qui peuvent être dessinés dans cette grille, les sommets
étant sur les points de croisement du quadrillage ? Et,
surtout, en quelle quantité ? Autre
formulation: combien de carrés peut-on former en reliant quatre points d'une
grille ? Carrés de deux types Les carrés droits
sont ceux qui sont alignés sur le quadrillage. Il
est possible de dessiner d'autres carrés; ce sont les carrés obliques. |
|
|
Voir Brève
48-942
|
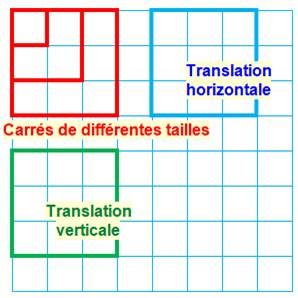
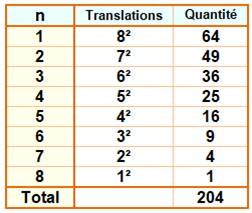
Décompte des carrés droits On
compte les carrés de taille n, n – 1, n – 2, … , 2, 1. (exemples en rouge) Ici,
il y a 8 ×
8 = 64 carrés de taille 1. Avec
le carré de taille 2, il y a 7 translations
horizontales possibles et 7 en vertical: soit 49 carrés de taille 2. Avec
le carré de taille 3, ce sera 6 translations et 36 carrés de taille 3. Etc. Quantité de carrés droits Il
s'agit de la somme des
carrés de 1 à n:
|
Types da carrés
Quantité de carrés selon le type
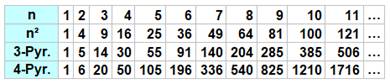
Voir Tableau pour
autres valeurs de n |
|
|
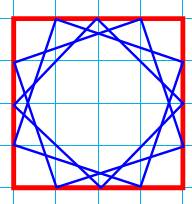
Quantité de carrés obliques inscrits dans un droit k × k Dans
le carré n × n, on choisit un "sous-carré" k ×
k. Les
sommets d'un carré oblique inscrit (bleu) sont nécessairement sur le
périmètre du carré droit (rouge). On
compte les possibilités (en bleu): k – 1 ou, k en comptant le carré droit
(bleus + rouge). Sur une grille k × k, il y a k carrés inscrits. Quantité de tous les carrés inscrits et internes Nous
venons de voir que le carré droit considéré compte k carrés inscrits droits
et obliques. Le
carré de taille inférieur en compte k – 1, et il est répété par translations
horizontales et verticales 2² fois. Le
carré de taille inférieur suivant en
compte k – 2 et il est répété par translations 3² fois. Etc. |
|
|
|
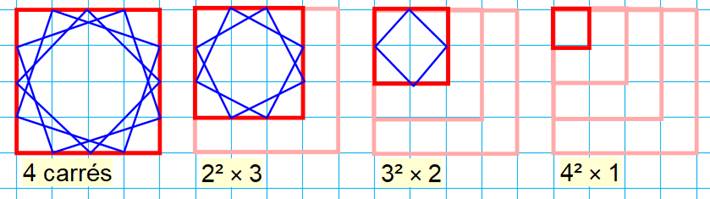
Principe du dénombrement des carrés dans le cas où n = 4 (N =
5)
Total: 4 + 18 + 11 + 16 = 50 carrés |
||
|
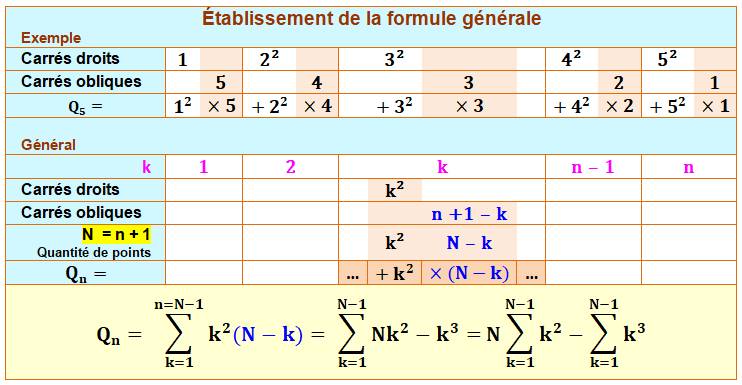
Formulation Établissement
pas à pas à partir de l'exemple de n = 5 carrés par côté (et N = 6, la quantité de points sur le
côté). On
introduit un indice k qui numérote les étapes (type carrés rouges) de 1 à n. Avec 5, il a cinq étapes ou cinq tailles
différentes de carrés.
Exemples de programme pour vérification
|
||
|
Somme des carrés & Somme des cubes Attention jusqu'à N – 1
=> signes moins Voir Somme des
carrés / |
|
|
|
Développement de la formule Exemple numérique Avec
n = 4 => N = 5 Qn = (54 – 52) / 12 =
(625 – 25) / 12 =
600 / 12 =
50 Avec
n = 9 => N = 10 Qn = (104 – 102) / 12 =
9900 / 12= 825 |
|
|
|
La
suite des nombres construite avec cette formule est donnée ci-contre. On
y retrouve bien 50 en position N = 5. |
|
|
|
Construction Ces
sont aussi les nombres pyramidaux de dimension 4. Ils
sont construits comme le cumul des nombres
pyramidaux à base carrée de dimension 3, eux-mêmes construis comme le
cumul des nombres carrés. |
|
|
|
Coefficient du binôme Le
nombre Qn est un coefficient dans le triangle de
Pascal. |
|
|
|
Combinatoire Quantité
de façons d'introduire deux paires de parenthèses entre N – 1 lettres |
Exemple: il
y a 6 cas pour 2 lettres ((a))b, ((a)b), ((ab)), (a)(b),
(a(b)), a((b)) |
|
Anglais: square pyramidal numbers, 4-pyramidal numbers
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Vidéos |
Vidéo YouTube: tapez le texte dans le moteur de
recherche
|
|
Cette page |
![]()