NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 02/12/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Géométrie
Débutants Géométrie	CONSTRUCTIONS				Glossaire Géométrie
INDEX Constructions Géométrie	Élémentaires	Triangles	Carrés	Yin Yang
		Cercle sans centre	Angles
	Collège	Sommaire de cette page >>> Index (Accès aux rubriques de cette page)

Constructions géométriques élémentaires

La panoplie de toutes les constructions de base apprises au collège. Indispensables pour la réalisation de constructions plus élaborées. Constructions avec règle, compas et dans certains cas avec rapporteur.

Un art de la géométrie consiste à oublier la règle graduée et le rapporteur, ce sont les constructions avec règle et compas uniquement >>>

Constructions géométriques – INDEX
Nom de la construction élémentaire suivis du (des) numéro(s) de page(s), puis du lien d'accès direct
GÉNÉRAL Perpendiculaire: 3, 4 >>> Parallèle: 10 >>> Milieu et médiatrice: 3 >>> Division du segment: 11 >>> Fraction >>> Angles 60°, 45° et 30°: 7 >>> Angle – Copie: 9 >>> Angle – Addition et soustraction: 9 >>> Angles égaux sur deux droites >>> Triangle: 13 >>> Carré: 12 >>> Carré inscrit dans le cercle: 12 >>> Rectangle: 12 >>> Parallélogramme: 10 >>> Pentagone: 21 >>> Hexagone: 8 >>> Rosace: 8 >>> Cercle – Centre: 19 >>> Cercle par trois points: 5 >>> Tangente au cercle: 20 >>>	TRIANGLES Trois côtés: 13 >>> Deux côtés et un angle: 15 >>> Un côté et deux angles: 14 >>> Trois angles: 14 >>> Rectangle: 16 >>> Isocèle: 17, 18 >>> Équilatéral: 8 >>> Hauteurs (orthocentre): 4 >>> Bissectrices (cercle inscrit): 6 >>> Médianes (centre de gravité): 5 >>> Médiatrices (cercle circonscrit): 5 >>> Cercle inscrit: 6 >>> Cercle circonscrit: 5 >>> Cercles exinscrits: 6 >>> AUTRES >>>

Perpendiculaires
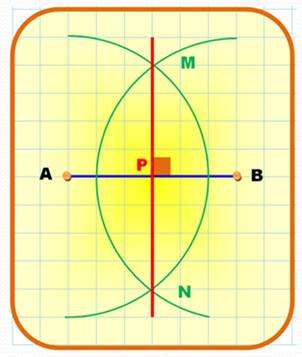
Perpendiculaire au milieu de AB: médiatrice Cercle de centre A, puis cercle de centre B de même rayon. Joindre les intersections M et N. Le point P, intersection de MN et de AB, est le milieu de AB. MN est perpendiculaire à AB.
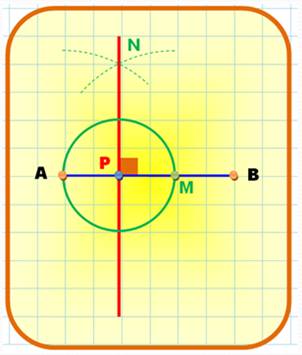
Perpendiculaire en P, un point de AB Cercle de centre P et de rayon AP, coupe AB en M. Médiatrice PN de AM. PN est perpendiculaire à AB.

Voir Perpendiculaire / Médiatrice / Cercle

Perpendiculaires et hauteurs
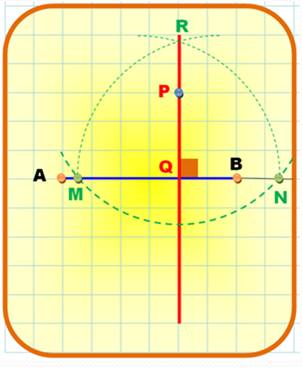
Perpendiculaire en P, un point quelconque Cercle de centre P qui coupe AB en M et N. Médiatrice RQ de MN. PQ est perpendiculaire à AB.
Hauteurs du triangle ABC Perpendiculaire en C à AB Perpendiculaire en A à BC Le point O d’intersection est le point de concours des hauteurs (orthocentre). La troisième hauteur BN passe également par le point O.

Voir Hauteurs

Médiatrices et médianes
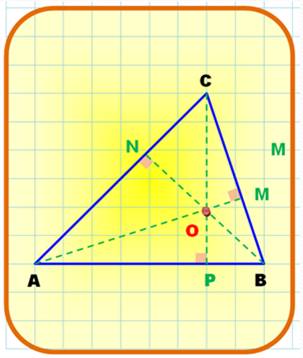
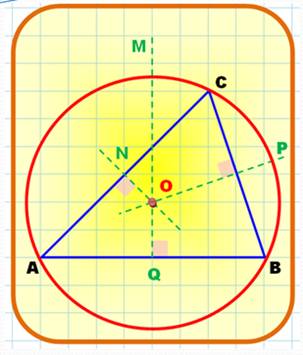
Cercle circonscrit au triangle Médiatrice de AB. Médiatrice de AC. Point d’intersection O. Le point O est le centre du cercle circonscrit au triangle ABC. La troisième médiatrice (de BC) passe également par le point O. Méthode qui permet également de construire le cercle passant par les trois points A, B et C.
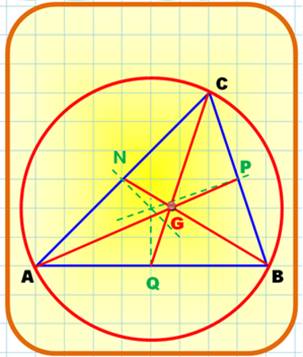
Médianes du triangle Avec la même construction: Les points N, P et Q sont les pieds des médianes AP, BN et CQ. Le point de concours G des médianes et le centre de gravité du triangle.

Voir Médiatrices / Médianes

Bissectrices
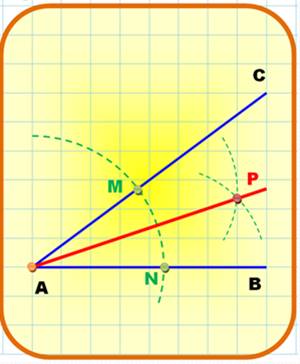
Bissectrice: partage de l’angle en A en deux angles égaux Cercle de centre A, qui coupe AB et AC en M et N. De M et N comme centre, cercles de même rayon qui se coupent en P. La droite AP est la bissectrice de l’angle BAC.
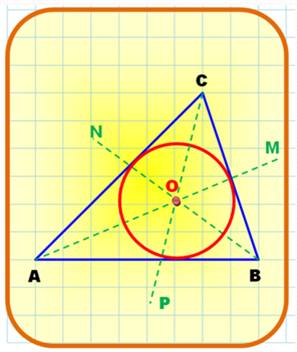
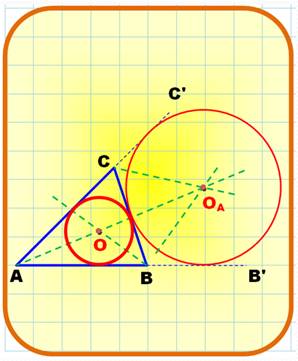
Centre du cercle inscrit à un triangle Bissectrice AM de l’angle en A. Bissectrice BN de l’angle en B. Intersection au point O qui est le centre du cercle inscrit du triangle ABC. La bissectrice CP de l’angle C passe également par le point O.
Trois centres exinscrits Prolonger AC et AB. Bissectrice de BCC’ et de CBB’ qui se coupent en OA. Le point OA est le centre d’un des trois cercles exinscrits du triangle ABC. Les trois triplets de ces bissectrices sont concourantes en OA, OB et OC.

Voir Bissectrices / Cercle inscrit et les autres

Angles 60°, 30° et 45°
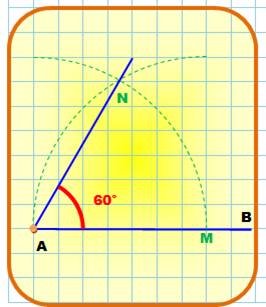
Angle de 60° Demi-droite AB, un côté de l’angle. Cercle de centre A, de rayon quelconque. Cercle de centre M de même rayon. Intersection en N. Angle MAN = 60°.
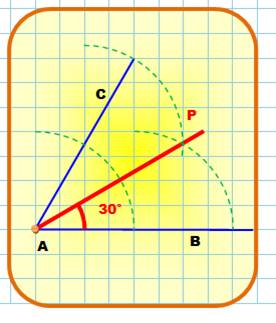
Angle de 30° Demi-droite AB, un côté de l’angle. Angle de 60° à partir de AB. Bissectrice. Angle PAB = Angle CAP = 30°.
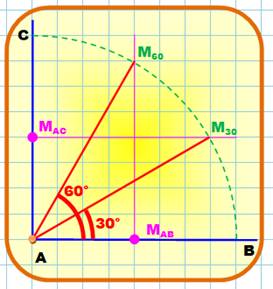
Angle de 30° et 60° en pratique Un quart de cercle avec AB et AC. Milieux de ces segments : MAB et AAC. Parallèles à ces segments en ces points Elles coupent le cercle en deux points qui définissent les angles de 30° et 60°. Construction utile pour situer rapidement ces angles dans le cercle, d’un simple coup d’œil. Voir Trigonométrie de ces angles
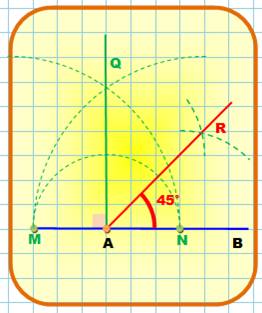
Angle de 45° Demi-droite AB, un côte de l’angle. Cercle en A qui coupe AB en M et N. Perpendiculaire en A à MN. Bissectrice de l’angle droit QAB. Angle RAB = Angle QAR = 45%. A l’œil, évidemment, il suffit de tracer la diagonale d’un carré.

Voir Angles

Triangles équilatéraux
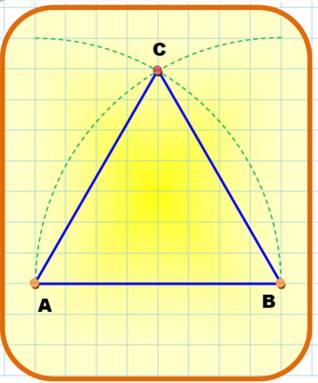
Triangle équilatéral Côté AB. Angle 60° en A. Angle 60° en B. Intersection en C. ABC est un triangle équilatéral.
Hexagone Triangle équilatéral ABC, à partir du côté AB. Triangle équilatéral, à partir du côté BC, etc. Le polygone en rouge est un hexagone (six côtés) réguliers (côtés et angles égaux).
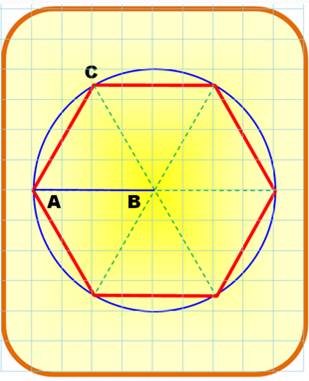
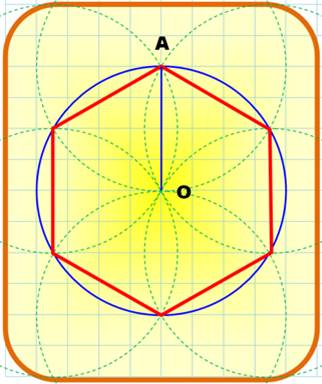
Hexagone et rosace Cercle de centre O et de rayon OA. Cercle de centre A de même rayon, puis cercles de même rayon avec pour centre la nouvelle intersection. Hexagone en rouge et rosace en pointillés verts.

Voir Triangle équilatéral / Hexagone

Angles
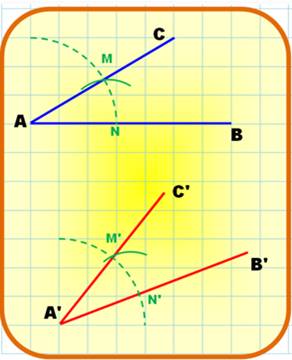
Copier un angle: BAC Dessiner une demi-droite A’B’. Cercle de centre A de rayon quelconque qui coupe les côtés de l’angle en M et N. Cercle de même rayon de centre A’ qui coupe A’B’ en N’. Avec le compas prendre la mesure NM. Cercle de centre N’ et de rayon la mesure prise (NM) qui coupe le cercle en M’. Tracer la demi-droite A’M’. L’angle B’A’C’ est la copie de l’angle BAC.
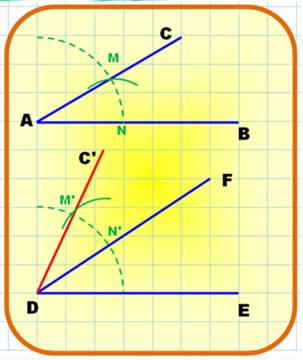
Additionner deux angles: BAC + EDF Copie de l’angle BAC à partir de DF qui joue le rôle de A’B’ (Selon les explications à gauche). Méthode semblable pour la soustraction

Voir Angles / Addition

Parallèles
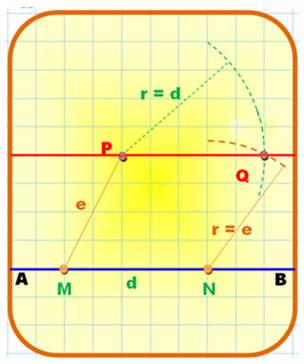
Parallèle en P à AB Deux points M et N sur AB (de préférence de part et d’autre de P). Cercle de centre P et de rayon MN = d. Cercle de centre N et de rayon MP = e Intersection en Q La droite PQ est parallèle à la droite AB. Autre solution Médiatrice de AP pour disposer du point M. Cercle de centre M de rayon MB, pour avoir le point Q. La droite PQ est parallèle à la droite AB.
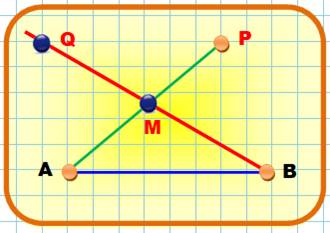
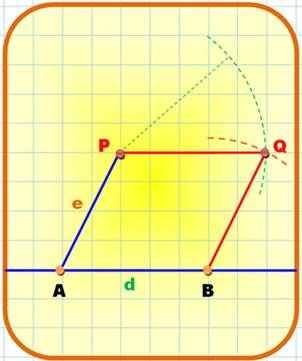
Parallélogramme avec A, B et P Cercle de centre P et de rayon AB = d. Cercle de centre B et de rayon AP = e Intersection en Q Le quadrilatère ABQP est un parallélogramme: AB = PQ = d et AP = BQ = e.

Voir Parallèles / Parallélogramme

Division du segment
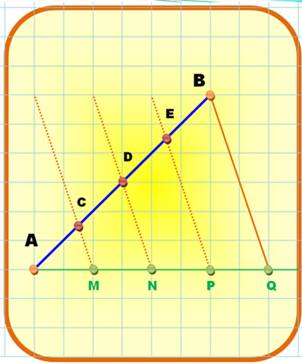
Division du segment AB en quatre parties égales Dessiner une demi-droite AQ. Avec un compas, marquer les points M, N P et Q à égale distance les un des autres. Relier BQ. Tracer les parallèles à BQ en P, N et M. Les points d’intersection C, D et E partagent le segment AB en quatre segments de même longueur.

Voir Division / Droite

Carré et rectangle
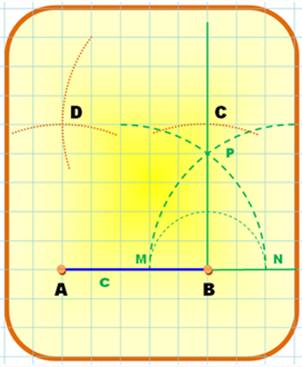
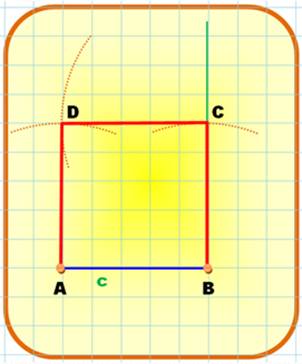
Carré de côté AB = c Perpendiculaire BP en B. Cercle de rayon c de centre B qui coupe la perpendiculaire en C. Cercle de rayon c de centre A et C qui se coupent en D. ABCD est le carré demandé. Rectangle Même type de construction en ouvrant le compas selon la longueur puis la largeur.
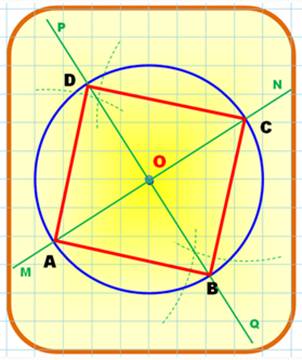
Carré inscrit dans le cercle Tracer une droite MN quelconque passant par le centre O. Perpendiculaire en O à MN. Les quatre intersections A, B, C et D avec le cercle sont les sommets du carré.

Voir Carré / Rectangle

Triangles – Côtés
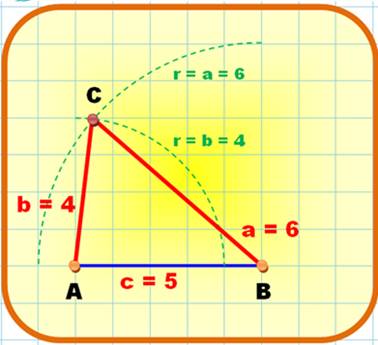
Triangle (a = 6, b = 4 et c = 5) Segment AB de longueur c = 5. Cercle de centre A et de rayon r = b = 4. Cercle de centre B et de rayon r = a = 6. Intersection en C. Le triangle ABC est le triangle demandé.
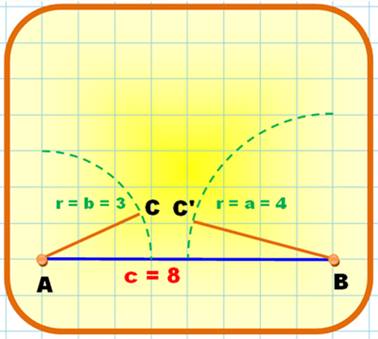
Triangle (a = 4, b = 3 et c = 8) Segment AB de longueur c = 8 (le plus long côté). Cercle de centre A et de rayon r = b = 3. Cercle de centre B et de rayon r = a = 4. Intersection impossible. C’est le cas chaque fois que c > a + b (inégalité triangulaire).
Cette construction est parfois baptisée (LLL) pour (Longueur, longueur et longueur); en anglais: (SSS) pour Side, side and side.

Voir Triangles / Construction des triangles / Résolution du triangle

Triangles – Angles
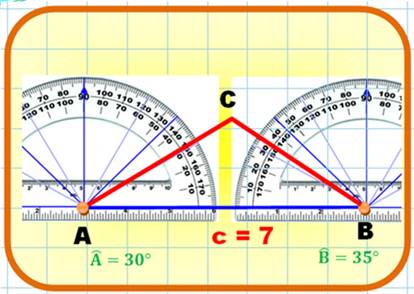
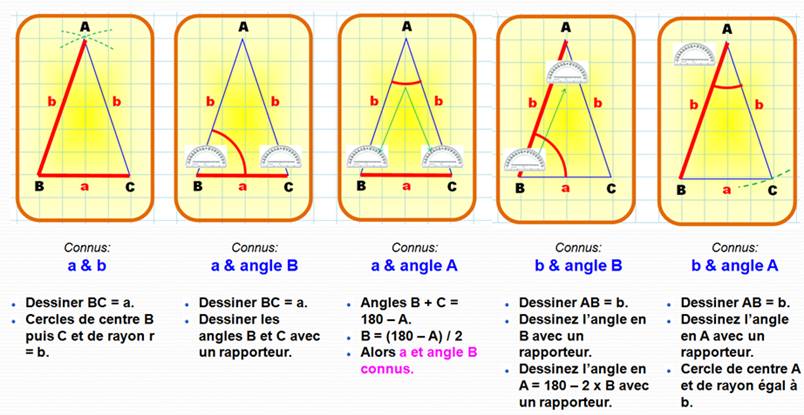
Triangle (c = 7; angles: 30° et 35°) Segment AB de 7 unités. Rapporteur pour 30° en A. Rapporteur pour 35° en B. Intersection en C. Le triangle ABC est conforme à la demande.
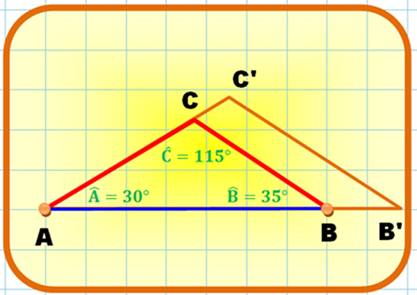
Triangle (Angles: 30°, 35° et 115°) Segment AB quelconque. Rapporteur pour 30° en A. Rapporteur pour 35° en B. Intersection en C, avec un angle en C = 180° – 30° – 35° = 115°. Le triangle ABC est conforme à la demande, MAIS, AB’C’ également. Il existe une infinité de solution selon la position de B.

Triangles – Angles (suite)
Triangle (a = 4, c = 7 et angle en A = 30°)
Solution n°1: ABC Segment AB de longueur c = 7 Cercle de centre B et de rayon a = 4 Rapporteur centré en A, aligné sur AB et trait AC à 30°. Le triangle ABC est le triangle demandé.	Solution n°2: ABC’ En prolongeant la demi-droite AC, elle coupe le cercle une seconde fois en C’ Le triangle ABC’ est un second triangle qui répond à la demande.

Triangle rectangle
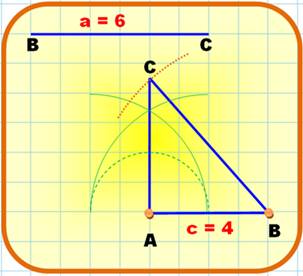
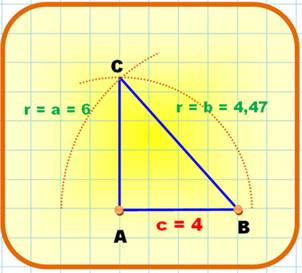
Triangle rectangle c = 4 et a = 6 (hypoténuse) Perpendiculaire à AB en A. Mesure de BC= a = 6 avec un compas. Cercle de centre B avec cette mesure, qui coupe la perpendiculaire en C. ABC est le triangle rectangle demandé.
Alternative Théorème de Pythagore dans le triangle. rectangle ABC donnerait: b² = a² – c² = 36 – 16 = 20 et b = 4,47 unités. Puis, construire le triangle dont on connait les trois côtés (a = 6, b = 4, 47 et c= 4). Note: le tracé des cercles est indiqué pour mémoire.

Voir Triangle rectangle

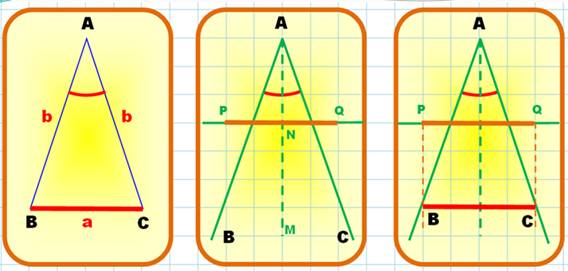
Triangle isocèle

Voir Triangle isocèle – Construction avec règle et compas

Triangle isocèle (a, A)
Connus: a & angle en A (alternative) Avec un rapporteur dessiner l’angle BAC connu en A. Bissectrice AM de l’angle BAC. Perpendiculaire en N (quelconque) à AM. Porter la longueur a/2 de part et d’autre de N: NP = NQ = a/2. Perpendiculaires en P et Q à PQ. Les points d’intersection B et C sont les deux autres sommets du triangle isocèle demandé.

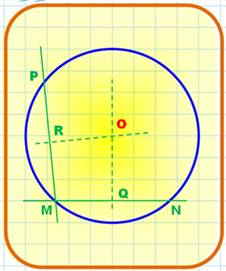
Centre du cercle
Centre du cercle (1) Un point M quelconque sur le cercle; deux droites MN et MP, issues de ce point. Leurs médiatrices (RO et QO) se coupent en O. Le point O est le centre du cercle bleu.
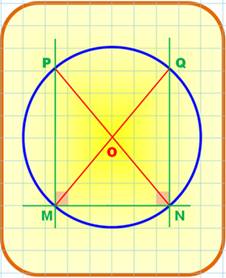
Centre du cercle (2) Une droite coupe le cercle en M et N. Perpendiculaires MP et NQ à MN en M et N. Tracer MQ et PN qui se coupent en O. Le point O est le centre du cercle bleu. Les triangles rectangles MNP et MNQ sont inscrits dans le cercle.
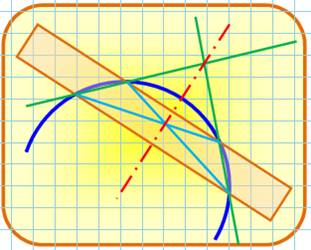
Centre du cercle avec une règle La règle à bords parallèles coupe la circonférence en quatre points. Deux paires de droites reliant ces quatre points (verte et bleue). Elles se coupent en deux points et, la droite (rouge) qui les réunit passe par le centre du cercle. L'opération est renouvelée pour obtenir une seconde droite. L'intersection avec la première est le centre du cercle.

Voir Cercle / Construction du centre (suite) / Cercle et les trois points / Théorème de Monge / Brève 341

Tangente au cercle
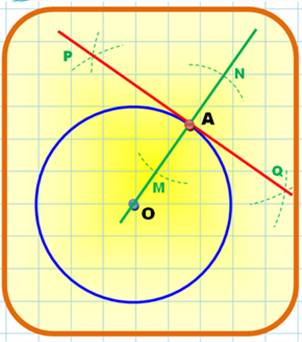
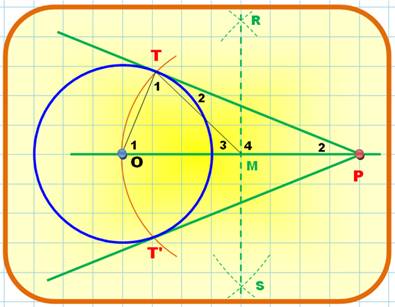
Tangente en A au cercle Cercle de centre O (bleu). Droite OA. Perpendiculaire PQ en A à OA. La droite PQ est la tangente en A au cercle initial. Tangentes à partir du point P externe Cercle de centre O (bleu). Droite OP. Médiatrice RS de OP. Cercle de centre M et de rayon OM. Intersections avec le cercle en T et T’. Les droites PT et PT’ sont les deux tangentes au cercle. Explications (angles repérés par un nombre) Triangle isocèle MOT: 1 + 1 + 3 = 180°. Triangle isocèle MPT: 2 + 2 + 4 = 180°. Somme: 1 + 1 + 2 + 2 + 180° = 180° + 180° 1 + 2 = 90° => OTP est un angle droit. 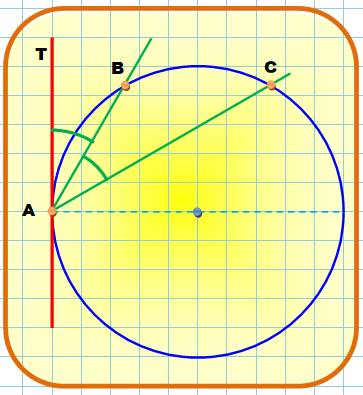Tangente sans le centre Arc de cercle (bleu; ici cercle complet). Le centre est non connu Point A quelconque. Point B et C tel que arc AB = arc BC. Angle BÂT tel que BÂT = BÂC. AT est la tangente en A au cercle. Cette construction est souvent intéressante même si le centre est connu. Explications Les angles BÂT et BÂC sont égaux (construction). Ils interceptent des arcs égaux. Pour BÂC, c'est l'arc BC. Pour BÂT, c'est forcément AB (= BC). L'angle qui intercepte l'arc AB est formé du segment AB et l'autre côté est nécessairement la tangente en A. Voir Tracé du cercle sans le centre

Pentagone
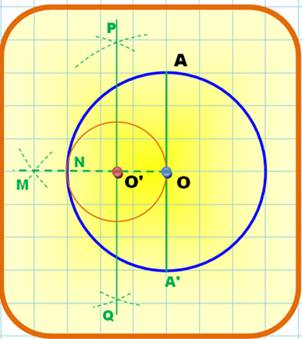
Construire O’ le milieu de ON Un cercle de centre O (bleu). Un diamètre quelconque AA’. Perpendiculaire OM à AA’. Médiatrice PQ de ON. Cercle de centre O’ et de rayon OO’.
Construire le pentagone Tracer A’O’. Cercle de centre A’ et de rayon A’R. Cercle de centre A’ et de rayon A’S. ABCDE est le pentagone régulier inscrit dans le cercle de départ.

Voir Pentagone – Construction détaillée et justification

Suite	Carré en rectangle Construction géométriques des nombres Constructions – Index
Voir	Carrés parfaits Constructible Construire les fractions Géométrie – Index Heptagone Quadrature du cercle Triangle de Calabi
Logiciel	Geogebra est un logiciel mathématique gratuit réalisant toutes ces constructions et bien plus … Euclidea – The Largest Collection of Interactive Geometric Puzzles – Jeux avec énigmes consistant à trouver la construction géométrique d'une figure.
Cette page	http://villemin.gerard.free.fr/Construc/ConsElem.htm