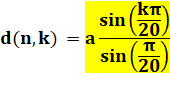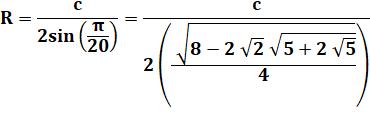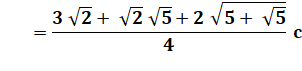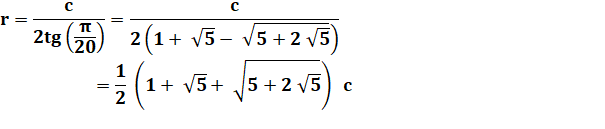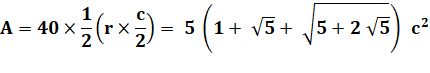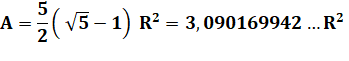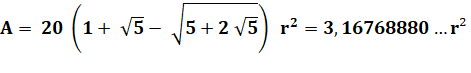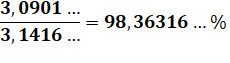|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
ICOSAGONE Icosagone: polygone à vingt
côtés ou vingt angles (du grec:
eikosi, vingt et gonia, angle). Icosaèdre: polyèdre à vingt
faces. Icosaèdre régulier: un des
cinq solides
platoniciens. |
Anglais: an icosagon is a 20-sided polygon / regular icosagon
|
|
||
|
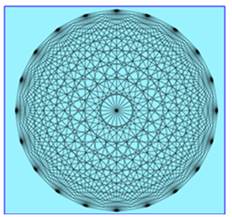
Quelconque Polygone
à 20 sommets, 20 côtés et 20 angles. Quantité
de diagonales: ½ 20 x 19 – 20 = 170. Régulier Somme des
angles: (20 – 2) x 180° = 3 240 ° Angle au
sommet: 3 240 / 20 = 162° Angle au centre
interceptant un côté: 360 / 20 = 18° L'icosagone
régulier est constructible. Étoilés Les trois polygones qui relient un sommet sur
trois, sur sept et sur 9. {3, 7 et 9} sont les trois nombres premiers
inférieurs à 20 et premiers avec 20. |
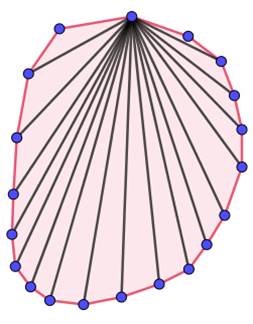
Icosaèdre convexe quelconque
|
|
|
Convexe: en parcourant
le périmètre dans le sens horaire par exemple, on pivote toujours vers la
droite pour tracer le côté suivant. Autre définition: le segment qui joint deux points
quelconques du polygone, y compris du périmètre, est toujours à l'intérieur du polygone. |
||
|
|
||
|
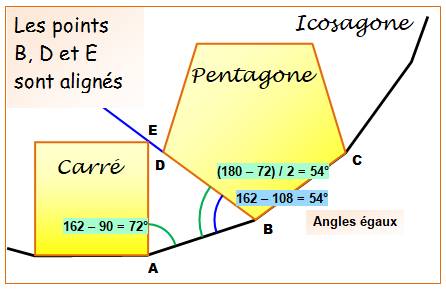
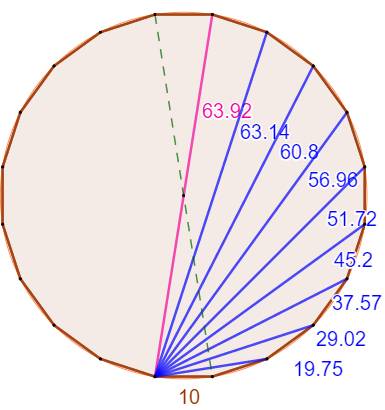
Un carré
et un pentagone
régulier construits sur les côté d'un icosagone. Montrer
que les points B, D et E sont alignés. Mesure de
l'angle ABE:
Mesure de
l'angle ABD
Les angles
ABE et ABD ont même mesure (54°), les points B, D et E sont alignés. |
L'angle en B est évalué de deux manières: avec ABE et avec ABD.
L'égalité montre que les trois points sont alignés. |
|
|
|
|||||||||||||||||||||||
|
Longueur
de la diagonale k, avec k la quantité de côtés interceptés par la diagonale. |
|
||||||||||||||||||||||
|
|
||||||||||||||||||||||
Voir Son calcul / Tables / Quantité
d'intersections des diagonales
Icosaèdre
régulier avec ses trois versions étoilées
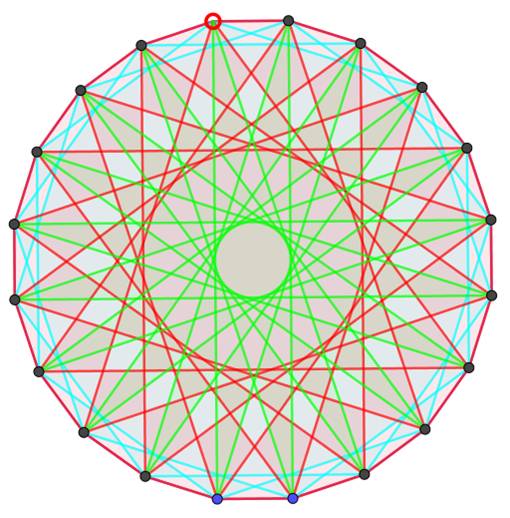
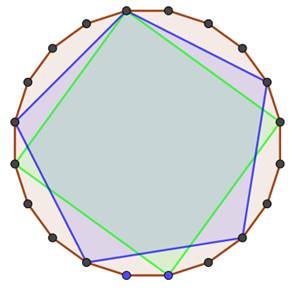
Icosagone
et triangles équilatéraux (tous les quatre sommets)
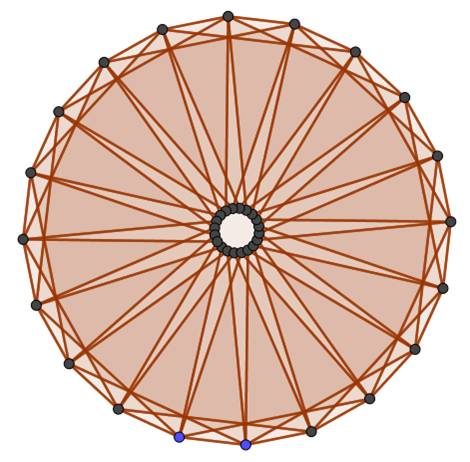
|
|
||
|
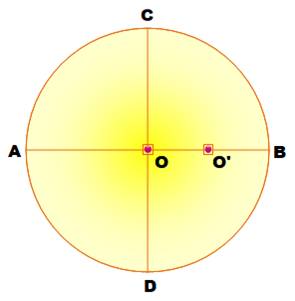
Étape 1 Construction
de la figure 1 par la méthode classique de construction
des médiatrices Le point
O est le milieu de AB et O' celui de OB. Étape 2 Tracez le
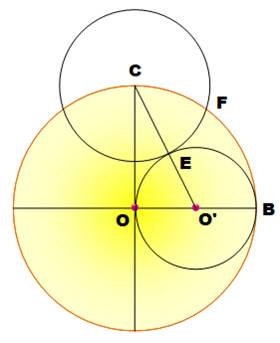
cercle de centre O' et de rayon OO'. Tracez le
segment CO' qui coupe le petit cercle en E Tracez le
cercle de centre C et de rayon CE qui coupe le grand cercle en F Étape 3 Tracez le
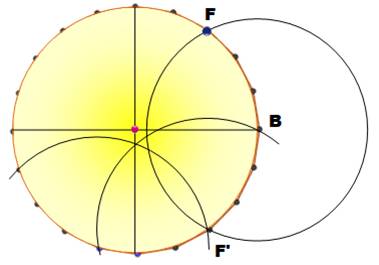
cercle de centre B et de rayon BF. Gardez
cette ouverture du compas Tracez le
cercle de même rayon à partir de chacun des nouvelles intersections avec le
grand cercle (comme F'). Les 20
sommets de l'icosagone sont ainsi définis tour à tour. |
Figure 1
Figure 2
Figure 3
|
|
|
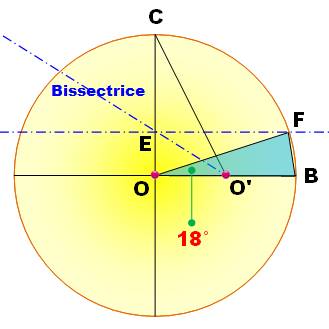
Autre possibilité Étape 1
identique. Tracez la
bissectrice de OO'C qui coupe OC en E. Tracez en
e la parallèle à OB qui coupe le cercle en F. L'angle
BOF vaut 18°. Pour
tracez l'icosagone, reportez la longueur FB de proche en proche. |
|
|
*Voir Construction
animée sur Icosagone
- Wikipédia
|
|
|||
|
Relation entre
|
|
||
|
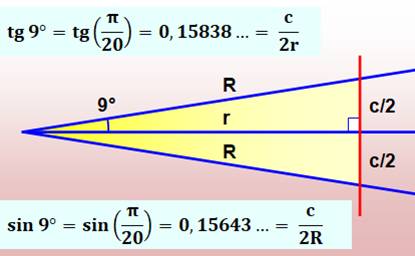
Cercles circonscrit (R) et inscrit (r) |
Voir Trigonométrie
de l'icosagone / Multiplication
par conjugué |
||
|
Aire de l'icosagone régulier |
À comparer à l'air du cercle: Ac =
3,14 … R² L'icosagone remplit le cercle dans cette
proportion:
|
||
Validation
des formules par mesures sur un icosagone (via Geogébra)
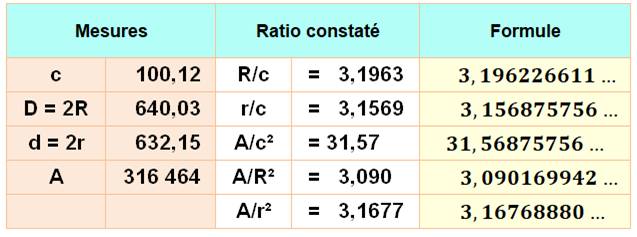
|
|
|||
|
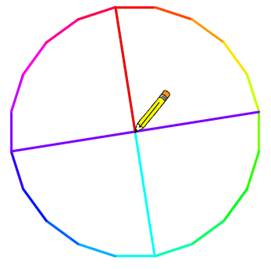
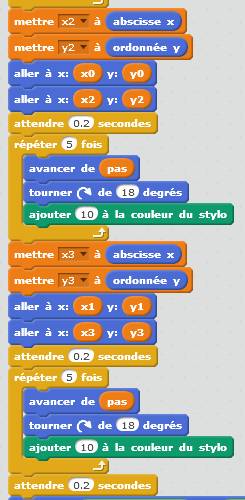
Ce
programme est très simple à réaliser Commentaires Le programme exécute 20 fois "avancer de la
quantité pas = 50" et
"tourner de 18° ". Pour tracer deux diagonales et le centre, quatre
couples de variables (x, y) sont mémorisés à la fin de chaque quart de tour
(5 côtés). Pour finir sur le centre, le crayon est envoyé au
milieu de l'une des diagonales. Dessin réalisé
|
|
Suite
|
|
|
Dernière instruction |
|||
Voir Programmation – Index / Programmation
du cercle avec Scratch
|
|
||
|
Les
colonnes doriques comportent vingt cannelures. Le Tholos
de Delphes compte vingt colonnes à sa périphérie. Construit vers 380-370
avant J.-C. Chaque colonne est creusée de vingt Le
swastika (illustration) est un
icosagone irrégulier. |
L'icosagone
(20) est le mariage du carré
(4) et du pentagone
(5) avec 20 = 4 x 5.
|
|
|
Livre de H.S.M. Coxeter, P. DuVal, H.T.Flather et
J.F. Petrie. Énumération des
stellations de l'icosèdre. Exemples
… |
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Polygone/Icosagon.htm
|
![]()