|
Édition du: 03/07/2021 |
|
INDEX |
TRIANGLES Éléments remarquables |
||
|
Éléments remarquables – Index |
|||
![]()
|
Éléments remarquables du triangle Centre de SPIEKER (X10) Spieker center / Spieker-Punkt Point
remarquable triangle: c'est le centre de masse du périmètre ou centre de
gravité des "tiges" homogènes donnant sa forme au triangle. On le
construit en prenant le centre du cercle inscrit au triangle médian. Theodor
Spieker (1823-1913) – Mathématicien allemand. |
||
|
|
Sommaire de cette page >>> Cercle de Spieker |
Débutants Glossaire |
|
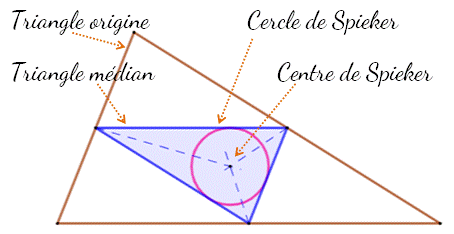
Construction Le triangle médian est construit en reliant les
trois points milieux des côtés du triangle. Le centre du cercle inscrit du triangle médian est le point de concours
des bissectrices (pointillés bleus). Une perpendiculaire en ce point à un des côtés
donne le point de tangence, ce qui permet de construire le cercle inscrit à
l'aide d'un compas. |
|
|
|
Centre de Spieker |
C'est aussi le centre de masse (centre
de gravité) du périmètre (périmètre formé de tiges d'un matériau
homogène). Chaque de ses droites découpent le triangle en
deux polygones (triangle et trapèze) de même périmètre. C'est le point de rencontre des trois droites-couperets
(cleaver) du triangle. |
|
|
Numéro |
Le centre
de Spieker est le point X10 de la classification de Kimberling. |
|
|
Coordonnées |
Trilinéaires: bc (b +c)
: ca (c+ a) : ab (a+ b) Barycentriques: b + c
: c + a : a + b |
|
|
Propriété |
Le point de Spieker (S), le centre du cercle inscrit
(I), le centre de gravité (G) et le point de Nagel (M) sont alignés et: IS = SM; IG =
2GS; MG = 2 IG. |
|
Anglais
|
The Spieker center of a triangle ABC is the
center of gravity of a homogeneous wire frame in the shape of triangle ABC |
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Remarqua/Spieker.htm
|