Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 28/03/2023 M'écrire Brèves de Maths

INDEX Graphe Topologie Dénombrement Logique	GRAPHES
	Graphes – Introduction	Arbres – Introduction	Chemin le plus court
	Chemin eulérien	Cinq pays	Voyageur de commerce
	Graphe planaire	Trois maisons	Multiple et diviseurs
	Graphe de Delaunay	Petit monde	Nombres de Delannoy
	Ivrogne	Colonies de fourmis

Faites un double-clic pour un retour en haut de page

VOYAGEUR DE COMMERCE Problème du commis voyageur Le problème P = NP Problème de recherche opérationnelle: Comment minimiser le trajet du voyageur de commerce allant de villes en villes. Problème d'une simplicité déconcertante. Mais d'une extrême complexité dès que croît le nombre de villes. Pourtant certains insectes, comme les abeilles, sont capables de résoudre ce problème >>> Plus généralement en mathématiques (informatique théorique), on cherche à savoir si la résolution d'un problème gourmand en capacité de calculs (NP) ne pourrait pas se réduire (toujours) à un problème plus simple (P) >>> Ona prouvé que le problème du voyageur de commerce est un problème NP-difficile, c'est-à-dire que son temps de résolution est exponentiel et qu'on ne pourra jamais trouver un algorithme en temps polynomial. Voir Dénouer les nœuds
	Sommaire de cette page >>> Le chemin en cercle >>> Voyageur de commerce >>> Solution >>> Problèmes polynomiaux >>> Problème P = NP >>> Les abeilles	Débutants Dénombrement Glossaire Combinatoire

Angl. Traveling Salesman Problem (TSP) / Hamilton Path Problem / Generalized Directed Rural Postman problem

(Traveling US ou Travelling UK)

Le chemin en cercles concentriques

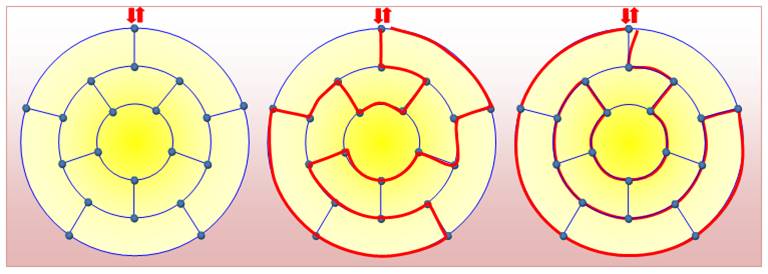
Caractérisation de l'énigme

La tournée d'inspection

Déplacement

Raisonnement

Classique

Primaire

Trouver le chemin permettant de passer sur chacun des nœuds du circuit, une seule fois, à la manière d'un poseur de prospectus qui doit visiter chacune des boites aux lettres ou celle d'un agent qui relève les compteurs d'électricité ou les compteurs d'eau. Quel est le chemin le plus court?

Deux solutions

Le parcours dessiné au centre est plus court que celui de droite (voir l’estimation donnée par le tableau =>). Remarquez que celui de droite procède selon un algorithme plus simple: faire la boucle externe, la boucle moyenne puis la boucle interne.

	Grand	Moyen	Petit
Au centre	3/5	6/10	3/5
À droite	4/5	8/10	4/5

Voir Cercles / Énigme des cercles qui tournent l'un sur l'autre / Cercles concentriques

Le voyageur de commerce – Caractérisation du problème
Avec ma voiture, je propose de raccompagner deux de mes amis – Alain et Bernard – chez eux. Je commence par Alain puis Bernard ou l'inverse	2 destinations 2 possibilités (combinaisons)
Le lendemain, aussi généreux, je propose aussi à Claude Alain puis Bernard puis Claude Alain puis Claude puis Bernard Bernard puis Alain puis Claude Bernard puis Claude puis Alain Claude puis Alain puis Bernard Claude puis Bernard puis Alain	3 destinations 6 possibilités (combinaisons) Calcul: 3 choix pour la première destination puis 2 pour la deuxième et 1 seul pour le dernier Soit N = 3 x 2 x 1 = 3!
En se serrant un peu la semaine suivante c'est Daniel qui nous rejoint Alain puis Bernard puis Claude puis Daniel Alain puis Claude puis Bernard puis Daniel Etc.	4 destinations 4! = 4 x 3 x 2 x 1 = 24 combinaisons
C'est un minibus qu'il me faut, ils sont dix cette fois …	10 destinations 10! = 10 x 9 … x 3 x 2 x 1 = 3 628 800 combinaisons
Avec 100!!! Le problème devient vite hors de portée de calcul	100 ! = 0, 933 10 ^158

Pour se donner une idée de ce nombre gigantesque

Même à la vitesse maximum des ordinateurs d'aujourd'hui.

Prenons 1 nanoseconde pour examiner une combinaison.

Il faudra 10¹⁵⁸ ns pour examiner le tout, soit 10 ¹⁴⁹ secondes.

À raison de 32 millions de secondes par an, soit en gros, 10⁷ secondes par an (en fait 3,15… 10⁷).

Il faudra 10¹⁴² années.

L'univers à 13 milliards d'années, soit en gros 10¹⁰ ans.

Il faudra 10¹³² fois l'âge de l'univers.

STOP!!!

Le voyageur de commerce – Solution

La solution donnant le chemin optimum du voyageur de commerce n'est pas simple. Durant les siècles passés, on publiait des guides pour aider à organiser la tournée. Il n'existe pas encore de solutions vraiment générales quel que soit le nombre de destinations ou les longueurs entre étapes. Ci-dessous, une méthode possible. Le voyageur de commerce souhaite passer par tous les points d'un parcours, en fait: par le trajet le plus court, sans passer deux fois au même endroit. Quel est le trajet le plus court qui passe par tous les points? Supposons que les points soient les sommets d'un parallélépipède à n dimensions. 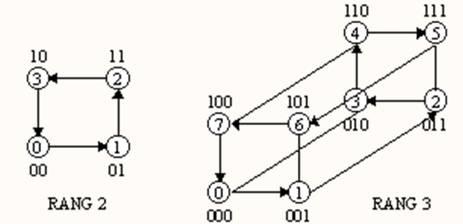On note les sommets 000...00, 000...01, 000...10, etc. On organise les longueurs du parallélépipède de la plus grande à la plus petite, et on commence par le sommet 000...00. Ce faisant, la généralité du problème n'est pas altérée. La solution est unique. Elle consiste pour le voyageur à passer d'un sommet à l'autre en utilisant le code Gros - Gray.

Par ordinateur

Adleman a réussi à construire un ordinateur à ADN qui a résolu une version du problème du voyageur de commerce. L'ordinateur à ADN a mis une semaine, là où un ordinateur classique aurait mis des années.

PROBLÈME POLYNOMIAL

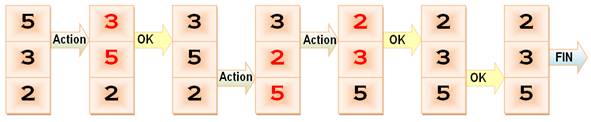
Problème de tri Trier un million d'articles devrait prendre environ 1 000 fois plus de temps que d'en trier seulement 1000. En fait, les programmes de tri les plus simples (algorithme du tri à bulles) prennent un temps proportionnel au carré du nombre d'articles à trier. Le tri à bulle consiste à faire remonter progressivement les plus grands éléments d'une liste par succession de comparaisons. Le pointeur désigne les deux premiers nombres de la liste, le programme constate que 3 est plus petit que 5, il doit remonter le 3. Action d'inversion des deux nombres. Le pointeur retourne en position initiale, le programme constate que les deux premiers nombres sont bien placés, et demande au pointeur de passer au couple suivant. Etc. Les théoriciens de la complexité ont pu démontrer que le programme de tri le plus rapide possible demanderait un nombre de pas proportionnel au nombre d'articles, multiplié par son logarithme. Problème polynomial Les problèmes dont la solution peut être calculée en une durée au plus proportionnelle à une puissance donnée de la taille du problème sont dits de type polynomial, ou P. A l'ère des ordinateurs, ils sont considérés comme faciles. Il existe alors un algorithme capable de trouver une solution effective en un nombre de pas de calcul inférieur à une fonction polynomiale de la taille des données d'entrée. NP = Nondeterministic Polynomial time: temps polynomial non déterministe   Problème du voyageur de commerce Trouver le chemin le plus court pour visiter une fois et une seule un ensemble donné de villes. Les meilleures solutions exactes que l'on ait trouvées viennent toutes à faire examiner par le programme la quasi-totalité des itinéraires possibles. Le nombre croît de manière exponentielle avec le nombre de villes. Voir  Solution du problème du voyageur de commerce Problème non déterministe Pour résoudre le problème du voyageur, on peut imaginer un ordinateur capable d'explorer simultanément tous les chemins possibles. Arrivé à un embranchement, la machine se divise en deux et emprunte simultanément les deux chemins. Dès lors, elle pourrait, en principe, résoudre le problème en un temps polynomial. Ces problèmes sont dits NP NP = Nondeterministic Polynomial time: temps polynomial non déterministe   L'implantation des composants sur un circuit intégré est de ce type. De même que le raisonnement automatique. La classe des problèmes NP sont ceux qui ne peuvent pas être résolus par déterminisme. Manière de dire qu'il faudra un nombre non déterminé de choix heureux pour atteindre une solution. Un problème est classé NP si une solution est trouvée malgré tout en un temps polynomial grâce à un algorithme devinant la solution et la vérifiant. Il existe des problèmes "plus" que NP, dit NP-complet (NP-complete) Performance des ordinateurs de bureau pour trouver la tournée optimale du voyageur de commerce: n = 10 voyageurs: quelques heures de calcul sans être sûr que la solution est optimale; n = 100 voyageurs: plus de 13 milliards d'années (âge de l'Univers). La durée est une fonction exponentielle de n. Dans la pratique On n'a jamais pu transformer un problème NP en une succession de problèmes de type P. On procède toujours avec des méthodes approximatives qui ne garantissent en rien la qualité de la réponse et sont même parfois très médiocres. Un des sept problèmes du millénaire est de savoir si un problème NP peut se ramener à des problèmes P.

Voir Heuristique / Exponentielle / Satisfiabilité / Algorithmes / Clay problems / Nombre de croisements d'un graphe

À retenir

Réussir à démontrer que P = NP ou au contraire que P ≠ NP constitue l'un des principaux problèmes ouverts de l'informatique fondamentale.

Tout l'enjeu est de savoir si

la classe de complexité P des problèmes admettant un algorithme de résolution s'exécutant en temps polynomial est équivalente à

la classe de complexité NP qui englobe les problèmes de décision dont la vérification du résultat, une fois celui-ci connu, demande un temps polynomial.

Problème P = NP
On distingue plusieurs catégories de complexité de résolution des problèmes: P: pour polynomiaux NP: non polynomiaux NP-complet NP-difficile La distinction P / NP date des années 1970. Il était évident que certains problèmes étaient plus faciles à résoudre que d'autres. La distinction entre les différents types de NP est une affaire d'experts.		Seuls les problèmes de type polynomiaux sont accessibles en un temps de calcul raisonnable. Les autres exigeraient des puissances de calcul inimaginables. À moins: de tomber directement sur la solution (chance); de trouver une astuce! de disposer d'une machine super-intelligente. Si cela peut arriver, la question devient: est-ce qu'il existe toujours une telle possibilité? Peut-on prouver qu'un problème NP est en dernière analyse une variante d'un problème P? Note: un problème P est "facile" à résoudre; une solution d'un problème NP est le plus souvent "facile" à vérifier. La question: les problèmes vérifiables en temps polynomial sont-ils aussi décidables en temps polynomial? Autrement dit, existe-t-il des problèmes dont les solutions sont faciles à vérifier mais sont dures à trouver ? Exemple: facile de vérifier que x = 1 est solution d'une équation du troisième degré; il est plus difficile de résoudre l'équation.
Le problème consiste à démontrer l'une des trois possibilités: P = NP P NP Non-démontrable		L'une des plus grandes énigmes mathématiques à l'heure actuelle. Un des plus fameux problèmes de mathématiques listé en 2000 parmi les sept problèmes du millénaire cités par la fondation Clay. La plupart des mathématiciens pensent que P est différent de NP. Quelques uns pensent le contraire et, il en est qui pensent que la question est indécidable.
La conjecture consiste à miser sur le fait que P = NP		P = NP Autrement dit: quelle que soit la complexité d’un problème, il en existerait toujours une solution simple. Si c'était le cas: il suffirait de mettre au point de meilleurs algorithmes afin de prouver que des problèmes complexes ne sont que des variantes de problèmes plus simples, problèmes que nous savons déjà résoudre avec les supercalculateurs actuels. Si P = NP, cela voudrait dire, en fait, qu’il existerait des solutions économiques à tous les problèmes connus.
En août 2017, Norbert Blum, mathématicien allemand, prétend avoir démontré que P NP. Mais, on a trouvé une erreur dans la démonstration (contradiction d'une hypothèse); admise par Blum.		P différent de NP Si c'était le cas: les problèmes complexes seraient fondamentalement différents des problèmes simples, et nos supercalculateurs ne risqueraient pas de résoudre les problèmes les plus complexes de sitôt.
Cas typiques de problèmes NP	Itinéraire du voyageur de commerce, organisation des tournées de livraison de colis; exemple ayant servi d'introduction à cette page. Mise au point du tableau de service d'un hôpital; Construction de l'emploi du temps d'un lycée; La combinatoire dans les jeux comme typiquement les échecs. Modélisation du jeu Candy Crunch; Cryptage des cartes bancaires: il mise sur le fait que les ordinateurs actuels sont incapables de craquer le code. Explication du repliement des protéines; compréhension qui pourrait permettre se soigner certaines formes de cancer. Etc.

Les abeilles et les bourdons

En 2011 et 2012, une équipe de Queen Mary (Université de Londres) prouve la capacité des bourdons à optimiser leur trajectoire pour butiner les fleurs.

Ils entrainent les bourdons à reconnaitre certaines fleurs et transplantent celles-ci dans la nature à plus de 50 mètres chacune. Les hyménoptères sont équipés de mini-transpondeurs qui permettent de suivre leur déplacement et les fleurs sont équipées de caméra à détection de présence.

Alors que le bourdon parcourt de l'ordre de 2000 mètre la première fois, sa trajectoire se réduit rapidement à 500 mètres. Parmi la centaine de routes possibles, rapidement elles en mémorisent une vingtaine seulement. Incroyable avec seulement un million de neurones.

Le but ultime des chercheurs était l'observation de ces animaux sociaux pour en tirer des principes qu'ils pourraient implanter dans des robots par mimétisme.

Voir Abeille / Parcours de l'abeille et Fibonacci

Suite	Le défi du métro parisien Marche de l'ivrogne Problème du sac à dos Les trajets – compter les itinéraires d'un point à un autre	Algorithme des fourmis Logique formelle Graphe – Index
Voir	Candy Crush Saga, un problème NP-complet Code Gray Énigmes et paradoxes Fractale Intelligence artificielle Jeux – Index	Morpion solitaire Parcours des abeilles Parcours du taxi Problème du pont de Königsberg Raisonnement Tour de Brahmâ
Sites	Voyageur de commerce - Algorithmes – Michel Van Caneghem – 2002 – pdf 7 pages Problème P = NP – Wikipédia Le problème P = NP, la complexité des algorithmes – Arnaud Durand – 2009 – Diaporama – 103 vues The shortest way to visit all metro lines in Paris** – Florian Sikora - September 20, 2017 – pdf 16 pages
Sites – Théorie	On the Generalized Directed Rural Postman Problem** – Michael Drexl – September 2012 On Some Generalized Routing Problem** – Michael Drexl – 2007 – pdf 178 pages
Cette page	http://villemin.gerard.free.fr/LogForm/GrVoyage.htm