|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
CERCLES CONCENTRIQUES Famille de cercles
ayant un centre
commun. La surface comprise entre
deux cercles concentriques s'appelle la couronne. |
Anglais: concentric circles / annulus
|
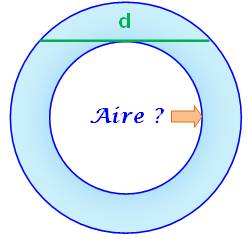
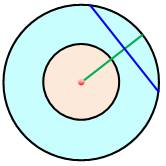
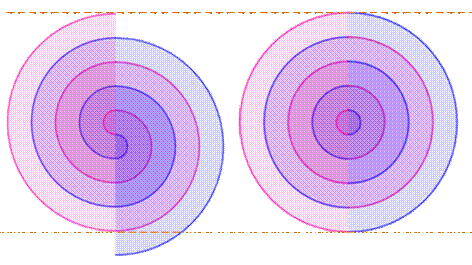
Question Quelle est la surface (l'aire) la plus grande entre la spirale
bleue ou la spirale rose. Construction Il s'agit du tracé de demi-cercles dont les extrémités se fixent sur
des points équidistants sur une verticale. |
|
|
|
|||
|
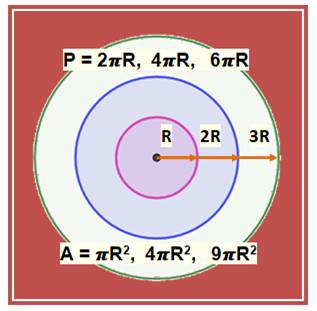
Ces trois cercles sont construits à partir du
même centre, ils sont concentriques. Avec des rayons en progression
arithmétique, le périmètre
progresse de la même manière, alors que, naturellement l'aire progresse comme
le carré du rayon. |
|
||
|
Exemple Un tuyau d'acier à un diamètre extérieur de 8 et intérieur de 7,6.
Mesures en centimètres. Quelle l'aire de la section en acier ? |
Aexterne = 3,14 x
(8/2)² = 50,26… Ainterne = 3,14 x
(7,60/2)² = 45,36… Acouronne = 4,90 cm² |
|
|
|
|
||
|
Aire de la couronne: Aire du disque bleu: Calcul de c avec théorème
de Pythagore.
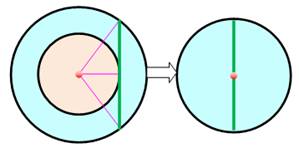
L'aire de la couronne est égale à celle du disque dont le diamètre est
la corde du grand cercle tangente au petit cercle. C'est l'aire séparant les deux traces d'un vélo décrivant un cercle
parfait ou même une courbe convexe quelconque. Le rayon r est alors la
distance entre les deux points de contact des roues. Voir Traces des roues de la bicyclette |
Astuce: pour
connaitre l'aire de la couronne alors que le disque central est inaccessible
(rempli de lave), il suffit de mesurer cette corde (2c). |
|
|
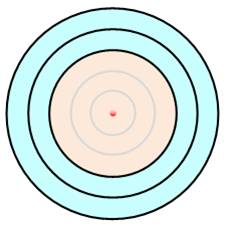
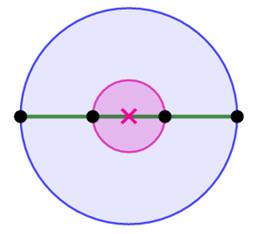
L'aire de la couronne bleue externe
est égale à celle du disque interne rose. Cette figure est souvent montrée comme une illusion d'optique
(the bull's eye illusion). Aire de la couronne externe:
Aire du disque bleu:
|
Illusion de l'œil de boeuf
Voir le
triplet: 3² + 4² = 5² |
|
|
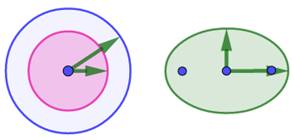
Si l'aire de la couronne est égale à celle de l'ellipse,
alors:
C'est l'équation du nombre d'or. Note: l'ellipse dorée est inscrite dans un rectangle
doré. |
Aire couronne
= aire ellipse => ellipse dorée
|
|
Voir Aire
du secteur, segment / Ellipse
dorée: construction…
|
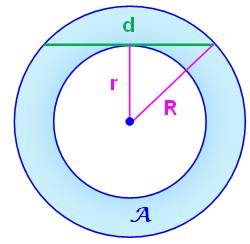
Construction Deux cercles concentriques délimitant une couronne. Une corde
du plus grand cercle est tangente
au plus petit. Connaissant la longueur de la corde, déterminer l'aire
de la couronne. Piste On sait calculer l'aire
des deux disques. Leur différence est l'aire de la couronne. Les deux rayons dessinés en rose forment un triangle
rectangle dans lequel on peut appliquer le théorème
de Pythagore. Calculs
|
Couronne et corde
Notations
|
|
|
|
||
|
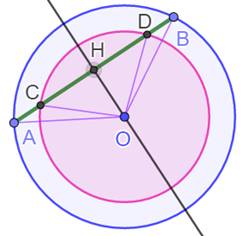
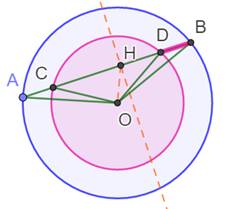
Une corde quelconque (AB) intersecte le petit cercle concentrique en C
et D. Les segments découpés sont de mêmes mesures On trace la médiatrice du segment AB. Elle passe par le centre du cercle.
C'est le cas aussi de la médiatrice de CD. Par symétrie, on a: OA = OB
& OC = OD HA = HD
& HC = HD et par soustraction: AC = BD |
Toute
corde découpe des segments égaux dans la couronne. |
|
|
|
||
|
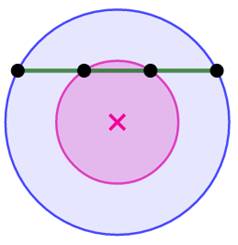
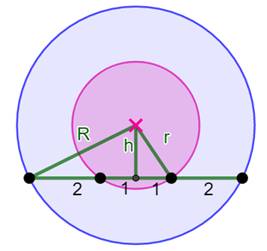
Question Quelle est l'aire e la couronne (bleu clair) ? Construction Deux cercles concentriques. La corde complète (verte) mesure 6 unités. Les quatre points sur la corde sont équidistants. |
|
|
|
Cas de la corde en position de diamètre Corde-diamètre: 6. Rayon du grand cercle: 3 Aire grand cercle: Rayon du petit cercle: 1 Aire petit cercle: Aire de la couronne: |
|
|
|
Cas d'une corde quelconque Utilisation du théorème
de Pythagore. Aire de la couronne: Évaluation de R: R² = h² + 3² Évaluation de r: r² = h² + 1² Aire de la couronne:
Aire de la couronne = constante |
|
|
|
|
||
|
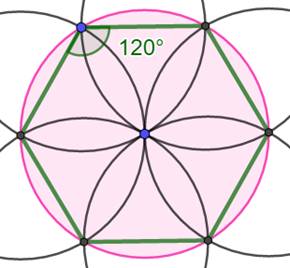
Corde dans un cercle Quelle est la probabilité que la corde d'un cercle soit plus grande
que le rayon du cercle ? Le tracé de l'hexagone
(rosace)
donne immédiatement la solution. Son côté est égal au rayon. Pour tout point A, sommet de l'hexagone, la corde est plus grande que
le rayon si elle est tracée dans l'angle au sommet de l'hexagone, lequel
mesure 120°. La probabilité vaut:
|
|
|
|
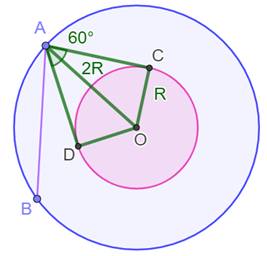
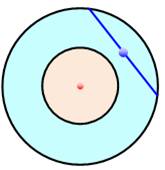
Corde et deux cercles concentriques: Quelle est la probabilité qu'une corde du grand cercle (comme AB)
coupe le petit cercle ? C'est le cas pour tout point A si la corde est comprise dans l'angle
formé par les tangentes de A au petit cercle (dessin en vert). Du fait de la tangence, l'angle en C est un angle droit et le triangle
AOC est rectangle. Ainsi:
La probabilité vaut:
|
Probabilité que la corde AB rencontre le petit cercle: 1/3 Pas que ! Certains disent 1/2 et d'autres 1/4 … Voir ci-dessous |
|
Voir Probabilités / Paradoxes
|
|
||
|
Il existe différentes manières de choisir la corde; elles conduisent à
des probabilités différentes. C'est le paradoxe de Bertrand. Joseph Bertrand
(1822-1900) décrit ce paradoxe dans son livre: Calcul des Probabilités en 1889.
P = 1/3
P = 1/2
P = 1/4 |
Rayon médiatrice
Milieu de la corde
|
|
|
|
||
|
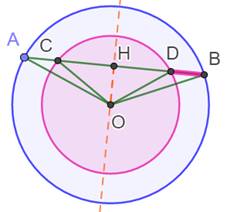
Construction
Quelle est la direction de cette sécante maximisant la longueur des
segments découpés dans la couronne ? Solution Le dessin du bas montre la situation favorable: la perpendiculaire en
H à la sécante passe par le centre des cercles. Longueur de chaque segment:
|
Situation quelconque
Situation optimale
|
|
|
Couper la figure au niveau de la verticale centrale
et faire glisser
|
Retour / Jeux et énigmes –
Index
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Livre |
|
|
Sites |
|
|
Cette page |
![]()