|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
PROBABILITÉS ET LOGIQUE Curieux,
non ? Allons voir … |
Voir Probabilités
|
|
||
|
|
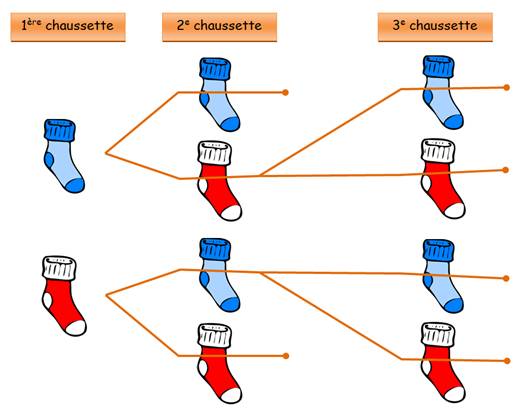
Réponse On répond fréquemment 25, alors que la réponse juste
est 3. En effet, si j’ai trois chaussettes en main, j’ai
forcément une paire. |
|
|
Illustration
Question
complémentaire Combien dois-je en tirer
pour être sûr d’avoir deux chaussettes de couleurs différentes? Réponse 25, car, si je n'ai pas de
chance, je tire toutes les chaussettes rouges (ou bleues) et en 25e
position arrive une chaussette de l'autre couleur. |
||
Voir Jeux et énigmes – Index / Trois
dés dans une urne / Principe des
tiroirs
|
|
||
|
Énigme Dans une
boite, vingt-quatre chaussures sont mélangées, douze vertes et douze rouges. Elles
vont par paires de couleur comme de pieds. Combien
de chaussures faut-il tirer en aveugle pour obtenir une paire bien assortie:
une paire rouge, ou une paire verte ? Solution Dans la
boite se trouvent: 12 paires de chaussures: 6 paires rouges et 6 paires
vertes Le cas le
plus critique: on tire 6 RG puis 6VD (ou l'inverse: 6RD et 6VG) avant de
pouvoir former une paire. Pour être
sûr d'avoir une paire assortie, il faut tirer 13 chaussures. Auteur: Martin Gardner (1914-2010). |
Solution illustrée
(1) Pas de chance du tout: on tire
toutes les chaussures rouges
gauches (RG) et toutes les chaussures vertes droites (VD). (2)
Le tirage suivant permet, à coup sûr, de créer une paire verte (2) ou une
paire rouge (2'). Évidemment,
la majorité du temps, on disposera d'une paire assorttie bien avant. |
|
|
|
||
|
Sur 100 hommes politiques au moins un est honnête.
Parmi deux hommes pris au hasard, il y en a toujours au moins un qui est
malhonnête. Combien sont malhonnêtes? |
Réponse: 99 Chaque fois que je couple l’honnête homme (il y en a au
moins un) avec un autre, cet autre est forcément un malhonnête. Donc tous les
autres sont malhonnêtes. |
|
|
|
||
|
Énigme Un sac contient
un jeton blanc ou noir, on ne sait pas. On y ajoute un jeton blanc. Sachant
que l'on vient de tirer un jeton blanc, quelle est la probabilité de tirer un
nouveau jeton blanc ? Solution Du fait
du tirage blanc, il faut considérer trois cas:
Auteur: Lewis Carroll (1832-1898) |
Après le premier tirage d'un blanc, celui que je viens d'y mettre ou celui qui y
était s'il était blanc, alors reste trois cas possibles pour le jeton restant
dans le sac. Dans
deux cas sur trois il est blanc. La
probabilité et donc de 2/3. (et non 3/4 comme le dirait un calul un peu
rapide) |
|
Voir Jeton pile ou face
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
![]()