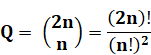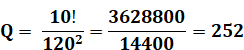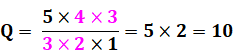|
||||||||||||||||||||||||||||||
![]()
|
Elle
c'est pile, et lui s'efface. C'est au poil, il met la gomme. |
Voir
Pensées & humour
|
PILE ou FACE Une décision à prendre, un choix à faire:
Un bon moyen de s'en sortir consiste à jouer à PILE OU FACE. Effectivement,
avec une pièce normale, les deux possibilités, pile et face, ont une
PROBABILITÉ ÉGALE. C'est donc un bon moyen de trancher un différend à deux
options. On retrouve cette dualité
à la roulette: pair / impair ou rouge / noir … Voici un bon moyen de décider, selon ma
grand-mère: jouez votre choix à pile ou face. Si le hasard donne un choix que
vous regrettez, prenez l'autre. |
|
Sur
une table, dans le noir, sont disposées 10 pièces dont 2 faces et 8 piles. Il
vous est demandé de trouver une solution pour faire deux tas, de tailles quelconques,
avec toutes les pièces et autant de faces dans les deux tas. |
|
|
|
|
Les cinq pièces Avec cinq pièces lancées ensemble, quelle
est la probabilité d'obtenir au moins quatre pièces du même côté. Dénombrement. Total des possibilités: 2 pour la première
pièce, 2 pour la suivante … Au total: 2 x 2 x 2 x 2 x 2 = 25 = 32. Parmi elles:
Probabilité P = cas favorables / total des cas = 12 /
32 = 3 / 8. |
|
Henri Dudeney (1857-1930)
|
Très
tôt (avant 10 ans), il s'intéresse aux problèmes d'échecs et |
Suite de sa biographie / Contemporains
|
|
|
|
Les deux pièces Si on lance deux pièces de monnaie, quelle
est la probabilité de tirer face au moins
une fois?
Historique On lance une seule pièce, deux fois de
suite (ce qui revient au même). Ce problème fut posé par d'Alembert en 1754. Il raisonna
ainsi:
Erreur de raisonnement bien sûr!
C'est le paradoxe de d'Alembert. Ce cas est représentatif de nombreux
cas subtils semblables ou voisins, dont le paradoxe
des deux sœurs. |
|
|
|
|||
|
Extraordinaire ou non ?
Le résultat de chaque lancer est
indépendant des précédents. La probabilité d'obtenir pile ou face lors
d'un lancer quelconque est toujours de 1/2 même
si on a déjà obtenu que des piles ou que des faces précédemment. Avec plusieurs pièces, chaque pièce tombera
sur pile ou sur face avec une probabilité de 1/2 pour chacune. Chaque pièce
vit sa vie! Aucune influence de l'une sur l'autre. Il n'est pas improbable
qu'elles tombent toutes sur face. Probabilité d'obtenir quatre faces avec
quatre pièces
La probabilité d'obtenir 4 faces de suite
est: (1/2)4 = 1/16 C'est aussi la probabilité d'obtenir 4
piles ou PFPF ou encore toute combinaison de 4 piles ou faces. Illustration |
|||
|
|
Avec 4 pièces:
Avec n pièces:
Au loto
1 2 3 4 5 6 ou 2 4 6 8 10 ou 1 2 4 8 16 32
… ne sont chacune qu'une combinaison comme
une autre, avec la même probabilité
de sortir. |
||
|
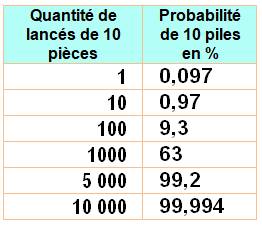
Probabilité de 10 piles avec 10
pièces Avec un seul lancer de 10 pièces, toutes en même temps, la probabilité
de trouver une configuration de 10 piles est quasi-nulle. En revanche avec énormément de lancers, la probablité de
trouver parmi eux une configuration de 10 piles devient un événement
quasi-certain. À partir de 5 000 lancers de 10
pièces, on est quasiment sûr d'obtenir au moins une configuration de 10 piles parmi tous ces lancers. Formule
|
|
||
|
|
||||
|
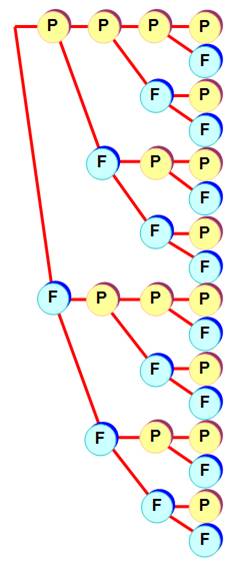
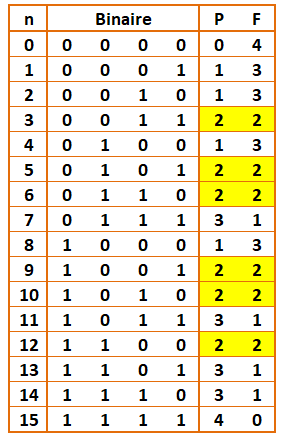
Avec 4 pièces, combien de fois 2 piles et
2 faces exactement ? Nous disposons de quatre pièces. Notons 0 pour Pile et 1 pour Face.
Lors d'un lancer, nous formons alors des nombres binaires de quatre bits. À chaque lancer, la configuration
des Piles et des Faces correspondra à un nouveau mot binaire ou à un mot déjà
rencontré. Avec une infinité de lancers,
chacune des configurations sera représentée un même nombre de fois (lois des
grands nombres). Il y a 24 = 16
possibilités. Le mot binaire de quatre bits peut
donc prendre 16 valeurs. On compte la quantité de 1 (Piles) et la quantité de
0 (Faces). Le tableau montre la présence de six
cas pour 2 Piles et 2 Faces exactement. |
Avec 4 pièces: 6 cas pour 2 faces et 2
piles exactement
|
|||
|
Liste pour 2n pièces avec n de chaque
sorte exactement |
[2, 2], [4, 6], [6, 20], [8, 70], [10, 252], [12, 924], [14, 3432], [16,
12870], [18, 48620], [20, 184756], … OEIS
A000984 |
|||
|
Formule Combinaisons
de n objets parmi 2n |
|
|||
|
Exemple Combinaisons de 5 objets parmi 10 |
Calcul par simplification de fraction
|
|||
|
|
|||
|
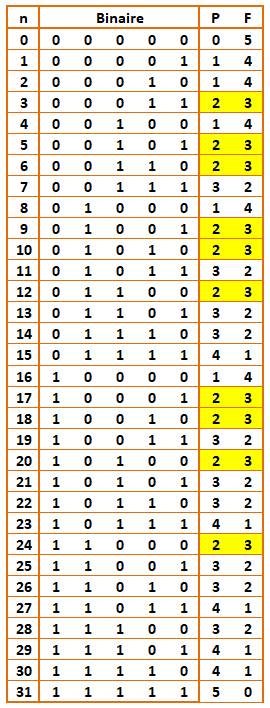
Avec 5 pièces, combien de fois 2 piles et
3 faces exactement ? Le tableau illustre la situation
avec ses 32 possibilités Nous dénombrons 10 cas avec 2 piles
et 3 faces exactement et réciproquement. |
|
||
|
Liste pour 2n + 1 pièces exactement n
piles et n + 1faces |
[1, 1], [3, 3], [5, 10], [7, 35], [9, 126], [11, 462], [13,
1716], [15, 6435], [17, 24310], [19, 92378], [21, 352716], … |
||
|
Formule Combinaisons
de n objets parmi 2n |
|
||
|
Exemple Combinaisons de 3 objets parmi 5 => n = 2 |
|
||
|
|
|||
|
Le joueur observe le déroulement des
lancers piles ou faces (pair et impair au casino). Il compte le surplus de fois que pile (ou
face) est arrivé. |
Quantité
de piles et quantité de faces = quantité n de lancers. Pn + Fn = n |
||
|
Le joueur déclenche ses paris dès qu'un
excédent lui convient (5 par exemple) |
Alors,
le joueur joue face (ou pile) jusqu'à ce que le surplus soit nul. Il
devrait gagner 5 fois sa mise initiale. |
||
|
Inconvénient majeur, le retour à l'équilibre peut être extrêmement long. |
De
plus, s'il s'agit d'un jeu de casino, la banque se rétribuera et annihilera le faible gain escompté. Martingale
à déconseiller ! |
||
Incroyable!
|
Au
jeu de pile ou face, nous avons une chance sur 8 de voir quatre fois le même
côté de la pièce:
C'est
beaucoup plus que ce que nous pensons généralement. Pour quelqu'un qui a
l'habitude (prof de proba. par exemple), il est facile de reconnaître une
suite de piles ou faces réelle par rapport à une suite qui serait imaginée
par le cerveau d'un homme. Celui-ci se censurera dès qu'il verra une certaine
continuité; il fera alterner les piles et les faces plus vite que le hasard
ne le ferait. |
|
Pour
les numismates, pile est le revers de la
pièce tandis que face est l'avers. Le côté
pile indique la valeur de la pièce. En 781, Charlemagne fait frapper son
monogramme, une croix, sur le revers.
Puis, à partir de la renaissance, les souverains y font figurer leur
portrait. Les
Anglais disent heads or tails, tête ou queue; Les
Allemands parlent de Kopf oder Zahl, tête ou nombre; Les
Espagnols, cara o cruz, face ou croix; Les
Italiens, testa o croce, tête ou croix. Pascal
utilisait l'expression: croix ou pile. Il prenait croix
pour Dieu dans son célèbre pari. |
|
Énigme Sur
une table, dans le noir, sont disposées 10 pièces dont 2 faces et 8 piles. Il
vous est demandé de trouver une solution pour faire deux tas, de tailles
quelconques, avec toutes les pièces et autant de
faces dans les deux tas. Solution Faites
deux tas avec 8 pièces et 2 pièces, puis retourner ces deux pièces. Exemple 1
Exemple 2
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Probabil/PileFace.htm |
![]()