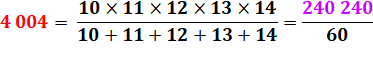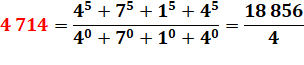NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/01/2025 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
Débutants Nombres		DicoNombre NOMBRES								Glossaire Nombres
1 10 100 500 1000 1500 1900 2000 3000		4 000 à 4 999								5000 10 000 20 000 50 000 100 000 10^6 10^9 10^100
		Quatre mille Anglais: Four thousand
4 000	4 100		4 200	4 300	4 400	4 500	4 600	4 700	4 800		4 900

4 000

Quantité	4 000 fois chacun des chiffres de 1 à 9 dans les nombres de 0 à 9999. Seulement 2 890 fois le "0".	>>>
Informatique	4004 Premier microprocesseur. Lancé le 15 novembre 1971. 740 Hz; 2300 transistors. Ce petit boitier remplace une ou plusieurs cartes électroniques de l'époque. Expédience vécue par moi-même, concepteur de tels circuits à l'époque. Le 8008 sera lancé en 1976.	>>>
Cosmologie	4 004 Âge de l'Univers selon James Ussher.	>>>
	4 104 exoplanètes détectées au 1^er janvier 2020.	>>>

4 002 = 23 x 174 = 58 x 69 5 886 = 9 x 654 = 18 x 327			Double produit pannumérique, le plus petit; suivi du plus grand.
					Motif avec factorielle tronquée. Coquetterie: répétition de chiffres.
4 030 = 130 x 31 = 310 x 13					Nombre EPRN.
4 031 = 2^3 + 3^3 + 5^3 + 7^3 + 11^3 + 13^3				Somme des cubes de six premiers consécutifs.
4 051	Il existe 4 051 façons de classer six éléments en suites ordonnées.
4 070 = 2 × 5 × 11 × 37		Exemple de décomposition d'une fraction en somme de fractions égyptiennes en utilisant l'algorithme glouton. Record de dénominateur.

4 095 = 2^12 – 1 = 90 × 91 / 2		Le plus grand nombre de Mersenne triangulaire.
4 095 = 3^2 x 5 x 7 x 13 4^n – 1 est divisible par 4 095 pour n = 6k		Diviseurs: 1, 3, 5, 7, 9, 13, 15, 21, 35, 39, 45, 63, 65, 91, 105, 117, 195, 273, 315, 455, 585, 819, 1365, 4095.
4 095 = 2^12 – 1^12 = 45 x 91		Divisible par 91 comme toutes ces formes en puissances de 12.
1+ 2 + 3 + … + 4 095 = 8386560 = 208 x 8!	La somme des nombres de 1 à 4095 est divisible par 8! = 40 320 Avec la somme des nombres jusqu'à n: S = n (n + 1) / 2:

4 096 = 2^12 = 1 000 000 000 0002 = 4^6 = 8^4 = 10 0008 = 16^3 = 1 0003 = CBA18 = 64^2	en binaire. en octal. en hexadécimal . 12, 11, 10 en base 18 (curiosité).
4 096 = 2^3 + 4 + 5	Opération avec chiffres successifs.
4 096 = 4^6 x 9^0	Opération avec ses chiffres.
	Carré et cube à la fois. Autres motifs semblables.
4 096 = 64^2 9 604 = 98^2	Motif avec permutation des chiffres.
	Puissances avec les chiffres de 4 096.
4 096 = 136² – 120² = 64² = 16² x 4² 4 096 = 514² – 510² = 64² = 32² x 2²	Nombre complètement carré.
4096 = 260^2 – 252^2 = 8^3 x 2^3 = 16^3	Différence de carré = produit de cubes.
4 096 = 585 x 7 + 1	Tout nombre carré et cube à la fois est de la forme 7k ou 7k + 1.
4 096 = (2 + 2i)^6 = (2 – 2i)^6	Entier = puissance de nombre complexe..
	Motif avec deux "4", contributeur du jeu du quatre 4.

4 100

Cosmologie

4 104 exoplanètes détectées au 1^er janvier 2020.

>>>

	Calculer rapidement cette somme. La réponse la plus fréquente est 5000, alors que la réponse exacte est 4100. Voir Additions fallacieuses Anglais: Tricky algebra sum riddle
4 104 = 16^3 + 2^3 = 4096 + 8 = 15^3 + 9^3 = 3375 + 729 = 18^3 – 12^3 = 5832 – 1728 = 2^3 x 3^3 x 19 = 6^3 x 19 4 104 + 12^3 = 18^3 = 5 832	Deuxième somme de deux cubes après 1729. Trois fois somme de deux cubes avec nombres négatifs autorisés. Ce nombre n'est pas un cube, mais contient un facteur premier en cube. Voir Table En ajoutant 12^3, on forme un cube qui devient ainsi somme deux fois de trois cubes.
4 123 = sigma(44²) = 1 + 2 + 4 + 8+ 11 + 16 + 22 + 44 88 + 121 + 176 + 242 + 484 + 968 + 1 936 = sigma(55²) = 1 + 5 + 11 + 25 + 55 + 121 + 275 + 605 + 3 025	Somme des diviseurs de 44² = 1 936 et de 55² = 3 025. Deux solutions pour n jusqu'à un million au moins.
4 140	Nombre de Bell (8^e).
4 150 = 4^5+1^5+5^5+0^5 4 151 = 4^5+1^5+5^5+1^5	Narcissiques de Keith Somme avec ses chiffres et ceux de ses puissances. Voir Table des nombres de Keith
4 181 = 37 x 113	19^e nombre de Fibonacci non premier bien que 19 le soit. Nombre de Markov.
4 195 = 5 x 839 4 196 = 2² x 1 049 4 197 = 3 x 1 399 4 198 = 2 x 2099 4 199 = 13 x 17 x 19	Plus petite suite de cinq nombres dont le plus grand facteur se termine par 9.

4 200

Géométrie

4 205: taille du premier carré parfait Trouvé en 1939 par Roland Sprague.

>>>

4 200 = 24 x 75			Nombre divisible par son retourné.
			4 225: plus petit nombre, 5 fois somme de 2 carrés, dont un avec 0. 8 125: plus petit nombre, 5 fois somme de 2 carrés, sans 0.
4 210	Semi-méandrique.
4 225	Ce nombre n'a pas de diviseur en 4k – 1 et neuf en 4k + 1. Record.
4 225 = 65² & 34 225 = 185²		Reste carré en lui ajoutant un chiffre à gauche.
400 = 20² et 5(4+0+0) = 20 2 025 = 45² et 5(2+0+2+5) = 45 4 225 = 65² et 5(4+2+2+5) = 65			Nombres dont la racine carrée est cinq fois la somme des chiffres.
4 225 = 97² – 72² = 65² = 13² x 5²			Nombre complètement carré.
4 225 = 0² + 65² = 16² + 63² = 25² + 60² = 33² + 56² = 39² + 52²			Plus petit nombre cinq fois somme de deux carrés avec 0. Sinon, c'est 8 125.
4 228 = 3×1^4 + 3×2^4 + 3^4 + 8^4 8 228 = 4×1^4 + 2×2^4 + 2×8^4			Plus petit nombre cinq fois somme de huit bicarrés. Suivants: 4403, 4468, 5443, 5508 … OEIS A345837 A noter ce cas avec un nombre semblable
4 240 = 2^12 + 12^2 = 4096 + 144			Nombre de Leyland.
4 244 = 2^7 x 3 x 11			Palindrome. Plus petit à neuf facteurs (répétitions comprises).

Géographie / Géologie	4 250 ans – Début de la période Meghalayen de la Terre. Nom complet de notre époque géologique: Phanérozoïque, à l’ére Cénozoïque, durant la période Quaternaire, à l’époque Holocène, âge Meghalayen.	>>>
Géométrie	4 257 triangles dans un hendécagone et ses diagonales.	>>>
Nombre	4 260 nombres premiers résistants par la gauche.	>>>

4 300

4 320	Fortement totient (ou hautement indicateur).
4 320 = 7! – 6! = 5 040 – 720 = 6² x 5! = 6! x 6	Différence de factorielles: toujours du type: (n+1)! – n! = n · n! = n² ·(n-1)!
4 356 = 66² = (2 x 3 x 11)² 5 476 = 74² = (2 x 37)²	Carré formé avec quatre chiffres consécutifs. Les deux seuls à quatre chiffres.
4 356 = 1^3 + 2^3 + … + 11^3	Somme des onze premiers nombres au cube.
4356 x 1,5 = 6534 = 4 x 1 089 43956 x 1,5 = 65934 439956 x 1,5 = 659934 …	Ce produit (nombre + sa moitié) donne le nombre retourné. Voir Nombre 1 089 Même motif sans fin avec un 9 intercalé. Même type avec 45 × 1,2 = 54.
4 359	Totient parfait.
4 375	Totient parfait.
4 343 = 2 110 968 / 486	Avec 2 110 968 = somme des facteurs les plus grands jusqu'à 4 343.
4 396 = 157 x 28	Produit pannumérique.

4 400

Unité

4 4448 m = 4,4448 km = 1 lieue = 1/20 du degré terrestre sur un grand cercle.

>>>

4 421 = 7! – 6! + 5! – 4! + 3! – 2! + 1!		Factorielle alternée.
4 425 = 1^5 + 2^5 + 3^5 + 4^5 + 5^5		Somme de puissance des nombres successifs
4 444 = 7 + 8 + … + 93 + 94		Repdigit: somme d'entiers consécutifs.
4 444 12² = 144 38² = 1444		N'est jamais la fin d'un nombre carré.
		Curiosité rare avec les décimales des racines carrées
etc.	Tous les repunits avec 2k fois le "4" ont une racine carrée qui commence avec 2k fois le "6".
4 464 = 4 x 6 x 186	Plus petit nombre en 4 et 6, divisible par 4 et 6.
4 472^12 ≈ 3 987^12 + 4 365^12 4 472^12 = 6,39… 10^43 3 987^12 + 4 365^12 = 6,39 … 10^43 Écart, tout de même: 1,21 … 10^33			Ce "presque Fermat" a été cité dans un épisode des Simpson (The Wizard of Evergreen Terrace).
4 480 = 8! / 3² = 9! / 9² = 9! / 3^4 = 9! / (9 x 9) = 362 880 / 81			Factorielle divisée Formule en trois 9

Calendrier

4713 av. J.-C. – 1er janvier Origine du calendrier des astronomes

>>>

4 500

4 500 = (1×5)^3 + (2×5)^3 + (3×5)^3			Somme de cube dans le ratio1, 2 et 3. Liste: 36, 288, 972, 2304, 4500, 7776, 12348, 18432, 26244, 36000, 47916, 62208, 79092, 98784, 121500, 147456, 176868, 209952, 246924, 288000, …
4 523		Première suite de quatre décimales de e = exp(1) qui forment un nombre premier.
4 536 = 9 x 9 x 8 x 7		Quantité de nombres de quatre chiffres avec chiffres tous différents. Notez la coquetterie avec 3, 4, 5 et 6.
4 545 = 5/6 x 5 454		Relation particulière avec son retourné.
4545 = 54540 / 12 45045 = 540540 / 12 … 454545 = 5454540 / 12 45454545 = 545454540 / 12 …			Nombre et son retourné. Motif infini. Autre motif également infini.
4 567	Premier horloge: les chiffres se suivent. Premier oscillant.
4567 => 5335	Chacun des chiffres est mis au carré et les chiffres obtenus sont soustraits pour donner 5335, un nombre palindrome. Ex: 4 => 16 => 6 – 1 = 5.
				Un des nombreux nombres heureux. Cycle des sommes des carrés des chiffres qui se termine par 1.

Géométrie	4 500 régions avec les diagonales de l'icosagone (20 côtés).	>>>
Histoire	4 500 m et Arche de Noé.	>>>
Transport	4 500 radars routiers en 2021.	>>>

4 600

4 608 = 2 . 48^2 = 9 . 2^9	Motif en double fois a . b^a.
4 624 = 4^4 + 4^6 + 4^2 + 4^4	Motif avec les chiffres en puissance.
4 649 x 1195 = 5 555 555 x 1434 = 6 666 666 x 1673 = 7 777 777 x 1912 = 8 888 888 x 2151 = 9 999 999	Générateur de repdigits par multiplications à 4 x 4 chiffres.
4 662 = 678 + 687 + … + 876 = 222 (6 + 7 + 8)	Somme des permutations des nombres formés des trois chiffres 6, 7 et 8.

Littérature

4 600 vaches – Pantagruel – Rabelais – 1532 Mais Pantagruel estant encores au berseau feist cas bien espouventables. Je laisse icy a dire comment a chascun de ses repas il humoit le laict de quatre mille six cens vaches. Titre complet: Les horribles et épouvantables faits et prouesses du très renommé Pantagruel Roi des Dipsodes, fils du Grand Géant Gargantua.

Romans

4 700

Géographie

4 700 m = 4, 7 km Horizon pour un homme de 1,73 mètre au bord de la mer.

Horizon

Cité par L'express-style mai 2011

Voir Sexe

4 714 = 2 x 2 357		Narcissique fraction (IJ Taneja).
4 727 = 2^2 + 3^2 + 5^2 + 7^2 + 11^2 + 13^2 + 17^2 + 19^2 + 23^2 + 29^2 + 31^2 + 37^2		Somme des carrés des douze premiers consécutifs.
4 753 = 1^3 + 3^3 + 5^3 + 7^3 + 9^3 + 11^3 + 12^3	Somme des sept premiers impairs au cube.
1 764 = 42^2 4 761 = 69^2	Motif avec permutation des chiffres.
4 762² = 22 676 644	Plus petit carré ayant les mêmes chiffres que son nombre. Suivants: 4 832, 10 376, 10 493 …

4 800

Géographie	4 807,81 m Altitude du Mont-Blanc en 2021. 4 808,72 m Altitude du Mont-Blanc en 2017. 4 810,90 m Altitude du Mont-Blanc en 2007. 4 792 m Altitude du pic rocheux recouvert par une calotte glacière décalée de 40 m à l'ouest. 4 807 m Altitude qui était officielle depuis 1863	Mont-Blanc Everest
Géométrie	4 850 diagonales dans un polygone à 100 côtés (hécatogone).	Polygones

4 832² = 23 348 224	Deuxième plus petit carré ayant les mêmes chiffres que son nombre. Précédent: 4 762; suivants: 10 376, 10 493 …
4 879² = 23 804 641 238 + 4641 = 4 879	Nombre de Kaprekar avec coupure en 3/5 et non au milieu (4/4).
4 884 = 76 x 66	Multiplication à 2 chiffres produisant le maximum de chiffres identiques.
4 888 = 2 + 3 + 5 + … + 223 + 227	Somme des 49 plus petits premiers. Curiosité de forme en 4 et 8.
4 890 = 1^6 + 2^6 + 3^6 + 4^6	Somme de puissance des nombres. Divisible par le nombre suivant 5; propriété générale.

4 900

4 900 = 70² = 1² + 2² + 3² + ...+ 24²	Seul nombre pyramidal carré, également carré. Trouvé par Lucas en 1875. Prouvé par Watson en 1918.
4901² = 4900² + 99² 24 019 801 = 24 010 000 + 9 801	Triangle pythagoricien.
	Appartient à une séquence récurrence en 49 et 99.
4 905 = 100 + 101 + … + 999	Somme des nombres à trois chiffres.
4 09510 = 77778= FFF16	Plus grand nombre à quatre chiffres en base 8 et plus grand à trois chiffres en base 16.
4 913 = 17^3 17 = 4 + 9 + 1 + 3	Nombre de Dudeney. Nombre digipuissant.
4 936 = 4 + 44 + 444 + 4444	Somme des nombres en 4.
4 940^3 = 3^3 + 17^3 4 941^3 = 13^3 + 14^3	Somme de deux cubes pour deux nombres successifs. Voir Nombre 854
4 950² = 24 502 500 2450 + 25000 = 4950	Nombre de Kaprekar
4 988 = MMMM DCCCC LXXX VIII	Le plus grand chiffre romain en taille.
4 999 => 4 + 9 + 9 + 9 = 31 6 899 => 6 + 8 + 9 + 9 = 32	Plus petit nombre premier dont la somme des chiffres est 31. Exemples de la conjecture: il est toujours possible d'obtenir k, non-multiple de 3, avec la somme des chiffres d'un nombre premier.

Physique

4 987 °C Température de la flamme la plus chaude. Oxygène + dicyanoacétylène (C4N2, sous-nitrure de carboné, non stable et à tendance explosive) 2 000 °C pour propane / oxygène 3 300 °C pour acétylène / oxygène 5 500 °C pour surface du Soleil.

>>>

Suite	Nombres 5 000
Voir	Nombre Chanceux Semaine Palindrome Triangle Tectroèdre Raisonnement Rep Unit Suites Nombre Têtus
Cette page	http://villemin.gerard.free.fr/NombDico/N1000/N4000.htm