|
Édition du: 08/07/2023 |
![]()
|
|
Nouvelle
orthographe avec
des traits d'union partout |
||||||||
|
![]()
Addition
et soustraction
|
350 =
2 + 73 + … + 26 |
|
|
350 = 44 + 46 + … + 56 = 7 + 73 |
|
|
350
= 1.2² + 2.3² + 3.4² + 4.5² + 5.6² |
|
|
350 = 5² × 14 351 = 3² × 39 352 = 2² × 88 |
|
|
|
|
Le plus petit cas pour six. Diviseurs de 350 Suite
ci-dessous |
|
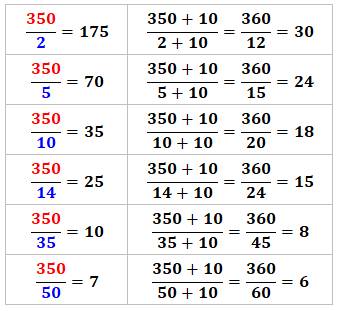
Nombres tels que n + k est divisible par certains de ses
diviseurs + k
|
Liste: ces nombres ne sont pas rares. En voici la liste pour k = 10 et pour
plus de deux occurrences jusqu'à 1000. En jaune l'exemple explicité
ci-dessus. [50, 3], [80, 3], [110, 3], [144, 3], [150, 3],
[170, 3], [200, 4], [230, 3], [270, 3], [276, 3], [290, 3], [320, 3], [350, 6], [390, 4],
[410, 3], [432, 3], [440, 4], [470, 3], [510, 3], [518, 3], [530, 3], [540,
4], [560, 3], [590, 3], [620, 3], [630, 4], [650, 5], [672, 3], [704, 3],
[710, 3], [770, 4], [782, 4], [800, 4], [830, 3], [840, 4], [870, 4], [890,
3], [900, 4], [935, 3], [950, 5], [980, 4], [990, 4]. |
|
Records d'occurrences jusqu'à 100
000 pour n+ k et d + k k = 1 [3, 1], [15, 2], [63, 3], [224, 4], [1539, 5],
[8855, 6], [73359, 7] k = 2 [4, 1], [10, 2], [40, 3], [70, 4], [448, 6],
[3078, 7], [17710, 8], [23560, 9] k = 3 [5, 1], [9, 2], [45, 4], [357, 5], [1152, 6],
[4617, 7], [9405, 8], [17952, 9] k = 4 [6, 1], [20, 2], [36, 3], [140, 5], [896, 7],
[5936, 8], [6156, 9], [23936, 10], [47120, 11] k = 5 [7, 1], [25, 2], [75, 3], [175, 4], [715, 5],
[2200, 6], [10075, 7], [10395, 9], [90475, 10] k = 6 [8, 1], [18, 2], [64, 3], [90, 4], [120, 5],
[330, 6], [624, 7], [2304, 8], [7050, 9], [9234, 10], [12474, 11], [35904,
12], [74250, 14] k = 7 [[9, 1], [33, 2], [105, 3], [273, 5], [1568, 6],
[6545, 8], [54873, 9]] k = 8 [10, 1], [28, 2], [64, 3], [112, 4], [280, 6],
[1792, 9], [11872, 10], [12312, 11], [47872, 12] k = 9 [10, 1], [28, 2], [64, 3], [112, 4], [280, 6],
[1792, 9], [11872, 10], [12312, 11], [47872, 12] k = 10 [12, 1], [50, 3], [200, 4], [350, 6], [2240, 7],
[4400, 9], [20790, 13] |
Avec les
puissances
|
350 = 5² + 10² + 15² |
|
|
350 = 13 + 23 + 53 + 63 |
|
La casse d'un
matériau avec le poing (japonais: shiwari) relève d'un pur problème de
physique: -
le poing doit se réduire à une partie
minimale de la main: articulation des phalanges de l'index et du majeur. -
la masse du poing au repos (600 g)
" pèse " 350 kg au
moment du choc, avec une vitesse de 60 km/h. C'est largement plus qu'il n'en
faut pour casser une pile de briques. -
au lieu d'impact, le matériau est comprimé,
alors que sa face inférieure, subissant une élongation, casse la première.
L'onde de choc poursuit le travail. Plus le matériau est dur, plus la casse devient un jeu d'enfant, avec... de l'entraînement tout de même. |
|
![]()
|
|
Voir Diviseurs, Quantité,
Somme,
Fonctions
arithmétiques
|
Numération: base, [chiffres] |
Repdigit (Brésilien) |
||
|
2,
[1, 0, 1, 0, 1, 1, 1, 1, 0] 3,
[1, 1, 0, 2, 2, 2] 4,
[1, 1, 1, 3, 2] 5,
[2, 4, 0, 0] 6, [1, 3, 4, 2] 7, [1, 0, 1, 0] 8,
[5, 3, 6] 9, [4, 2, 8] 10,
[3, 5, 0] 11,
[2, 9, 9] |
12, [2, 5, 2] 13,
[2, 0, 12] 14,
[1, 11, 0] 15,
[1, 8, 5] 16,
[1, 5, 14] 17,
[1, 3, 10] 18,
[1, 1, 8] 19,
[18, 8] 20,
[17, 10] 21,
[16, 14] |
22,
[15, 20] 23,
[15, 5] 24, [14, 14] 25,
[14, 0] 26,
[13, 12] 27,
[12, 26] 28,
[12, 14] 29,
[12, 2] 30,
[11, 20] 60,
[5, 50] |
24,
[14, 14] 34,
[10, 10] 49,
[7, 7] 69,
[5, 5] 174,
[2, 2] 349,
[1, 1] |
Voir Bases
/ Brésiliens
![]()
|
Retour Suite |
|
|
Voir |
|
|
Voir |
![]()