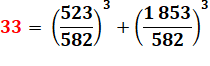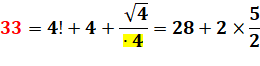Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 19/11/2024 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	… / 0,001 / 0,1		0 à 99			100 / 200 / 300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100 / Infini
	-0-	10		20	30		40	50	60	70	80	90
	30	31		32	33		34	35	36	37	38	39

Nombre 33	Maths générales du 33	Maths détaillées du 33	Nombre 33 insolite
			Expressions 33

Trente-trois

Thirty-three

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	10 0001
Bases	10203
Romain	XXX III

Suite

33 = 1! + 2 ! + 3 ! + 4!

Caractérisation du nombre

Blum (facteurs = 3 mod 4)

Chanceux

Composé

Composé inévitable (ou minimal)

Cunningham

Curzon

Déficient

Docile (amenable)

D-nombre

Idonéal

Impair

Narcissique de Keith

Palindrome

Palindrome en binaire

Proth

Queneau

Repdigit

Semi premier en triplet

Simple

Dodécagonal (3)

Voir

Nom des nombres

Nombres selon langues

Nombres selon bases

Fonctions arithmétiques

Exercices de prononciation en anglais et en italien Virelangue ou en anglais: tongue twister
Thirtythree thin Finns throw fortythree frogs into four Thracian theatres. Trente-trois Finlandais maigres jettent trente-trois grenouilles dans quatre théâtre de Thrace. Une des phrases anglaises pour exercice de prononciation (tongue twister).	Trentatré trentini entrarono a Trento tutti e trentatré trotterellando. Trente-trois habitants de Trente arrivèrent à Trente, les trente-trois en trottant et en se dandinant. Une des phrases italiennes pour exercice de prononciation.

J'ai l'âge du sans-culotte Jésus ;

c'est-à-dire 33 ans, âge fatal aux révolutionnaires."

Camille Desmoulins (1760 – 1794)

Voir Pensées & humour / Langue / Chiffres romains / Expressions avec 33

CARTE D'IDENTITÉ
Nombre	Composé	Département	GIRONDE
Facteurs	33 = 3 x 11	Élément	ARSENIC As
Pté Typique	33 = 1! + 2 ! + 3 ! + 4!	Mnémo	MAMAN
	Suite Maths		Suite Culture

PROPRIÉTÉS GÉNÉRALES

Numération	Les îliens du Détroit de Torrès comptent jusqu'à 33 (le petit orteil du pied droit) en passant par 8 (épaule droite), 26 (hanche droite) et 28 (cheville droite), ce qui donne une bas 33 pour leurs calculs.
Géométrie	33 régions créées par les côtés prolongés de l'octogone.	>>>
Jeux	33 = 99 – 66 = 62 – 29 Chaque terme avec son retourné sur une calculette (ex: 29 devient 62).	>>>
	33 ou 37 cases Au jeu classique du solitaire.	>>>
	33 allumettes pour dessiner 4 cubes adjacents.	>>>
	33 = a^3 + b^3 + c^3 solution trouvée en 2019 34 = 5^3 + (–4)^3+ (–3)^3 On connait les solutions pour une grande majorité des nombres. En 2017, on conjecturerait qu'elle n'existait pour 33.	>>>

Biologie	33 vertèbres Chez l'humain.	>>>
	33 chez le docteur.	>>>
	Le corps de la sangsue comporte 33 segments.
	Le rorqual bleu peut atteindre 33 m de longueur et peser 150 tonnes. Le plus grand et le plus gros animal de la planète.
Chimie	33 éléments chimiques connus de Lavoisier (1789). On en connaîtra le double en 1825.	>>>
Multimédia	Il faut composer le 33 pour atteindre la France au téléphone.
Construction	L'Empire State Building est situé entre la trente-troisième et la trente-quatrièmement rue dans la cinquième avenue de New York.	>>>
Histoire	33 de notre ère Mort de Jésus-Christ. Âge du Christ à sa mort.	>>>
	Les Trente-Trois insurgés à l'origine de l'indépendance de l'Uruguay, obtenue en 1828.
Géographie	Le royaume de Bahreïn est constitué de 33 îlots.
Social	La robe noire de l’avocat est ornée de 33 boutons. Ils représentent l’âge du Christ à sa mort. D’origine religieuse, la robe de l’avocat est au départ un symbole de dignité et de puissance.
Religion	Année 33 – Mort de Jésus-Christ.	>>>
	33 ou 99 grains d'ambre. du chapelet de l'islam.	>>>
	Que 33 jours de pontificat pour Jean-Paul I^er en 1978.
	Le roi des dieux (Indra) et 33 dieux princes chez les hindous Dieux des anciennes religions de Perse et d'Inde.	>>>

Autour du nombre

Nombre	33,3	33, 333… = 100 / 3 Tiers de 100.
Multimédia	33,3	Trente-trois-tours Disque 33 tours (ou disque vinyle). Long playing record (LP) – Langspielplatte. Disque dont la vitesse de rotation est de 33 1/3 tours par minute. Il y avait aussi des 45 tours et autrefois des 78 tours.	>>>
Histoire	33,5	33 h 30 min. Durée de la traversée de l'Atlantique par Lindbergh.	>>>

Propriétés MATHÉMATIQUES

Chiffres et numération

3310 = 1000012	Palindrome en décimal qui le reste en binaire. Le plus petit non trivial. Suivant: 9910 = 11000112 OEIS A007632
33 + 33 = 66 = T11	Devient repdigit et triangulaire en lui ajoutant son retourné.
33 = 30 + 03 = 12 + 21		Nombre sommes de retournés. Propriété générale des repdigits à deux chiffres.
33 = 3+3+3 + 5+9+3+7 33^3 = 35 937 33 = 3 +3 + 1+1+8+5+9+2+1 33^4 = 1 185 921		Narcissique de Keith Somme de ses chiffres et de ceux de son cube ou de sa puissance 4. Voir Table des nombres de Keith
33 = 0 + 1 + 6 + 1 + 6 + 5 + 6 + 1 + 6 + 1		Somme des unités des nombres à la puissance quatre.
3367 x 33 = 111 111 3367 x 66 = 222 222 3367 x 99 = 333 333 3367 x 132 = 444 444 3367 x 165 = 555 555 3367 x 198 = 666 666 3367 x 231 = 777 777 3367 x 264 = 888 888 3367 x 297 = 999 999		Motif avec 33 et ses multiples, formant les repdigits.
33		33 nombres de Harshad jusqu'à 100 compris.

Addition et soustraction

33 = 3 + 4 + 5 + 6 + 7 + 8 = 10 + 11 + 12 = 16 + 17			Trois fois somme de nombres consécutifs >>>
33 = 12 + 21 66 = 11 + 12 + 21 + 22			Somme des formes permutées distinctes à deux chiffres 1 et 2.
33 = 1 + 11 + 21			Troisième Nombre figuré d'ordre 12 (dodécagonal).
33 = 2 + 2 + 29 = 3 + 7 + 23 = 3 + 11 + 19 = 3 + 13 + 17 = 5 + 5 + 23 = 5 + 11 + 17 = 7 + 7 + 19 = 7 + 13 + 13 = 11 + 11 + 11				Plus petit nombre neuf fois somme de trois nombres premiers.
33	Plus grand nombre non somme de nombres triangulaires distincts.
33 = 1! + 2! + 3! + 4! = 1 + 2 + 6 + 24		Somme de factorielles. Toutes les sommes de factorielles à partir de là se terminent par 3.
33 = 4! + !4 = 24 + 9		Factorielle plus sous-factorielle. Forme palindrome.
33 = Triangles ?		Nombre non décomposable en somme de nombres triangles distincts. C'est le plus grand.

Multiplication, division, diviseurs

33 = 3 × 11		Nombre simple. Nombre composé. Repdigit. Palindrome. Voir palindrome à retard
33 = 3 × 11 34 = 2 × 17 35 = 5 × 7 36 = 2² × 3²	Quatre nombres consécutifs comportant deux facteurs distincts. Plus petit cas.
1 + 3 + 11 = 15 Somme des diviseurs propres < 33		Nombre déficient. Le plus petit terminé par 3.
		Motif avec factorielle tronquée.
Il y a 11 nombres premiers inférieurs à 33 et, 33 est multiple de 11		Nombre MulQprem.
33 × 34 = 1122 333 × 334 = 111222		Motif itératif
33 x 31 = 1023 33 x 7 = 231 33 x 70 = 2310 33 x 94 = 3102		Permutations des multiples de 33 à quatre chiffres, divisibles par 33.

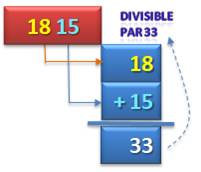
	Clé de divisibilité par 33. Constituer des blocs de 2 chiffres et les additionner. Le résultat doit être divisible par 33. Même méthode pour 99.
(33) = t(34) = t(35) = 4	Triplets de nombres consécutifs ayant même quantité de diviseurs. Le plus petit.
(33) = (35) = 48	Même somme de diviseurs pour deux nombres consécutifs de même parité. Liste: 33, 54, 284, 366, 834, 848, 918, 1 240, 1 504, 2 910, 2 913, 3 304, 4 148, 4 187 …
		Oméga est la quantité de facteurs distincts. Leur somme pour quatre nombres consécutifs est égale à 8. Le plus petit cas.
33 est semi-premier	33, 34 et 35 plus petit triplet de semi-premiers successifs.
33 | 10^33+1 – 1	Cas de divisibilité aussi observé pour: 3, 9, 11, 33, 77, 99, 143, 303, 369, 407, 707, 959, 1001, …

Avec les puissances

33 = 1² + 4² + 4² = 2² + 2² + 5² = 2² + 2² + 3² + 4² = 1^3 + 2^3 + 2^3 + 2^3 + 2^3 = 1^4 + 2^4 + 2^4 = 1^5 + 2^5	Toutes les sommes de puissances de 2 à 5 avec deux à cinq termes (sans doublons de 1).
33 = Aucune 34 = 16 + 9 + 4 + 4 + 1 35 = 9 + 9 + 9 + 4 + 4	Aucune somme de cinq carrés pur 33. Mais, tout nombre supérieur à 33 est somme d'exactement cinq carrés non nuls.
33 = 8 866 128 975 287 528^3 + (–8 778 405 442 862 239)^3 + (–2 736 111 468 807 040)^3 = (6,969… – 6,764… – 0,205…) 10^47	Solution trouvée en 2019 par Andrew Booker au problème de la somme des trois cubes.
33 = 1^5 + 2^5 = 11 x 3	Somme de puissance de nombres consécutifs, divisible par le nombre suivant. Propriété générale .
33 = 1^5 + 2^5	Somme de puissance 5 de nombres successifs.
33 = 7² – 4² = (7 – 4) (7 + 4)	Dénombrement des cases du solitaire.
33 = 0^0 + 1^1 + 2^2 + 3^3	Somme de puissance et nombre identiques.
33 = 17² – 16² = 17 + 16 = 7² – 4²	Différences de carrés. Début d'une suite pour les repdigits. Motif général pour tout nombre impair.
	Somme de deux cubes rationnels.

En puissance

33² = 1089 et 10 + 89 = 99 99² = 9801 et 98 + 01 = 99 66² = 4356 et 43 + 56 = 99	Autour des nombres de Kaprekar. Tous les repdigits en 9 sont Kaprekar d'ordre 2. Les nombres en 3 et 6 ont leurs sommes correspondantes en 9. Voir Brève 634
33² = 55² – 44² = 65² – 56²	Curiosités avec différences de carrés. Aussi avec 333, 3333, …
33² = 1089 99² = 9801	Motifs palindromique: le carré de son symétrique est le symétrique de son carré.
33² = 1122 – 33 333² = 111222 – 333	Curiosité qui produit un motif répétitif. Voir Nombre 333
33² + 12² = 1 233 33² + 88² = 8 823	Motifs avec coquetterie: 12 + 88 = 100.
33^2 = 1 089 33^4 = 1 185 921 33^6 = 1 291 467 969 33^7 = 42 618 442 977 33^8 = 1 406 408 618 241 33^12 = 1 667 889 514 952 984 961	Jamais de chiffre 3 dans toutes ces puissances de 33.
33^2 = 1 089 33333^2 = 1 111 088 889 33…3^2 = 11…108…889	Tous les 3-repdigits au carré ne comportent jamais les chiffres {2, 3, 4, 5, 6, 7}.
33^3 = 35 937 333^3 = 36926037	Tous les 3-repdigits au cube ne comportent jamais les chiffres {1, 4, 8}.
Rang, Nombre, Son Cube
33^10 = 1 531 578 985 264 449	Plus petite puissance 10 avec les chiffres de 1 à 9.
2^33 = 8 589 934 592 => 599 359 premier	La suite des chiffres impairs forme un nombre premier. Voir Nombre 20

Dénombrement, jeux et curiosités

	Jeu du quatre 4. Avec la notation anglaise: .4 = 0,4 = 2/5 Plus petit nombre nécessitant cette astuce.
33	Nombre chanceux d'Ulam.

Autour du nombre

33! – 1 = 0,868331761… 10³⁷

Générateur de nombre premier factoriel.

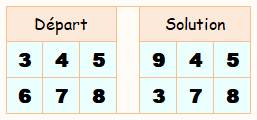
Voir Jeux et puzzles

Énigme (à gauche) de l'inversion

Soit les deux rangées de cartes suivantes.

Bouger seulement deux cartes pour avoir la même somme sur les deux rangées.

Solution (à droite)

Ah oui! Il faut retourner une carte

La somme 3+4+5+6+7+8 = 33 n'est pas divisible par 2.

Alors que 3+4+5+9+7+8 = 36 est divisible par 2.

33 dieux dans les anciennes religions védiques:

33 Deva Symbolisent l'ordre, la vérité. Gouvernent le ciel, l'air et la terre. Disposent de pouvoirs bénéfiques pour l'humanité.

et les Asura Symbolisent le désordre, le mensonge. Veulent s'approprier les pouvoirs divins. Sorte de diables.

Voir Hindous

Littérature

21 février 1933, je suis dans ma trente-troisième année. Trente-deux fois j'ai passé le jour et l'heure de ma mort comme on passe devant la porte d'une maison qu'on habitera un jour et qu'on ne pense même pas à regarder. Julien Green

Voir Pensées & humour

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 0, 0, 0, 0, 1] 3, [1, 0, 2, 0] 4, [2, 0, 1] 5, [1, 1, 3] 6, [5, 3] 7, [4, 5] 8, [4, 1]	9, [3, 6] 10, [3, 3] 11, [3, 0] 12, [2, 9] 13, [2, 7] 14, [2, 5]	15, [2, 3] 16, [2, 1] 17, [1, 16] 18, [1, 15] 19, [1, 14] 20, [1, 13]	10, [3, 3] 32, [1, 1]

Voir Bases / Brésiliens

Suite	Voir le menu en haut de page Nombre 33 insolite Nombre 34
Voir	Primorielle Cristaux Palindrome retard Solitaire
Site	Références Internet
Cette page	http://villemin.gerard.free.fr/NombDico/Nb30a50/Nb33.htm

Renvois de liens

>>> MOTIF 34

>>> NOMBRE 34

>>> NOMBRE 35

>>> EMBOUTEILLAGES

>>> GRILLE MAGIQUE

>>> VERTÈBRES

>>> CYCLE DE VIE

>>> INDE