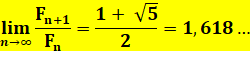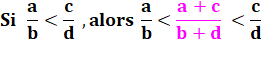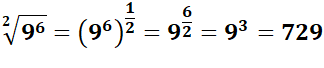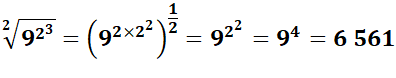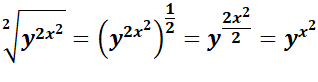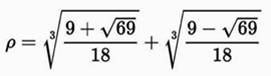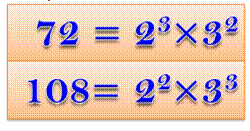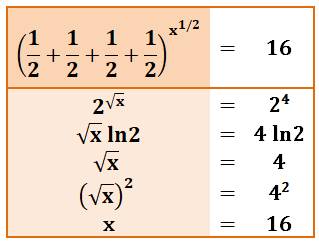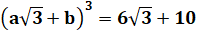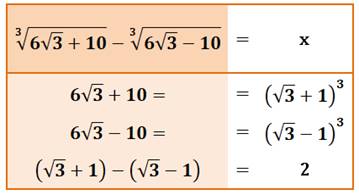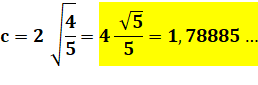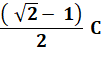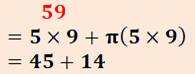|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
BRÈVES de MATHS – Page 32 Un millier de faits et chiffres sur les nombres et les
mathématiques
En principe ces pages sont très abordables sans
connaissances particulières de maths. Elles sont proposées dans un ordre
quelconque favorisant la découverte de sujets multiples. |
Anglais: Facts and figures about numbers and mathematics
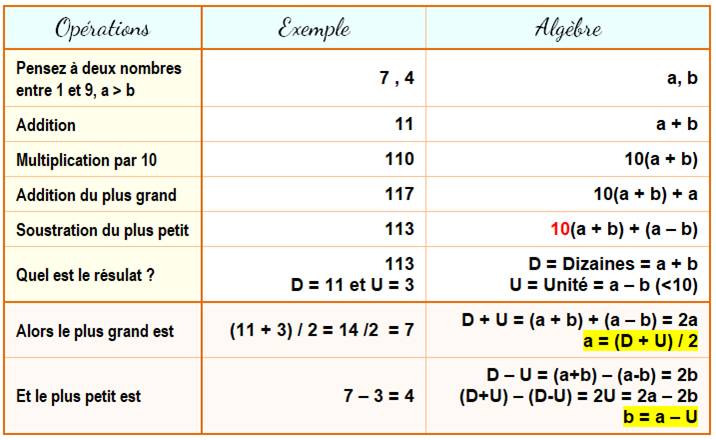
620. Magie – Devinez deux nombres |
|
||
|
Extension aux
nombres à deux chiffres en multipliant par 100. |
|||
|
Brèves associées |
>>>
Deviner
quatre nombres consécutifs |
>>>
Brèves Magie – Index |
|
|
Pour en savoir plus |
>>>
Les quatre opérations |
>>>
Magie – Index |
|
621. Magie – Danemark |
|
||||
|
Le tour |
Exemple |
||||
|
Prendre un nombre quelconque. Multiplier par 9. Retirer 5. Ajouter les chiffres. Recommencer pour obtenir un
seul chiffre. |
123 456 1 111 104 1 111 099 1+1+1+1+9+9 = 22 2 + 2 + 4 |
||||
|
Associer ce chiffre à la
lettre correspondante dans l'alphabet. Trouvez un pays d'Europe
commençant par cette lettre. Sans que tu me dises quoi
que ce soit |
4 => A, B, C, D Danemark
|
||||
|
Vous aurez retenu la
propriété de la preuve par 9. Le nombre multiplié par 9
donnera En retranchant 5, nous
aurons toujours Le tour n'est faisable
qu'une seule fois ! |
|||||
|
Brèves associées |
>>>
Deviner
quatre nombres consécutifs |
>>>
Brèves Magie – Index |
|||
|
Pour en savoir plus |
>>>
Preuve par neuf |
>>>
Magie – Index |
|||
622. Pavage et Fibonacci |
|
|||
|
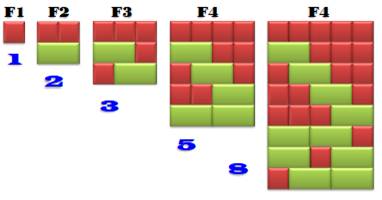
La suite de Fibonacci: 1, 1, 2, 3, 5, 8, 13 … Chacun est la somme des deux précédents. Une utilisation des nombres de Fibonacci: pavage sur une longueur n avec
des dalles carrées (1x1) ou rectangulaire (1x2). La quantité de possibilités
pour n donné est le nombre Fn de Fibonacci. |
|
|||
|
Brèves associées |
>>>
Les
nombre de Fibonacci |
>>>
Brèves Suites – Index |
||
|
Pour en savoir plus |
>>>
Suite de Fibonacci |
>>>
Pavage dominos |
||
623. Fibonacci et nombre d'or |
|
|||
|
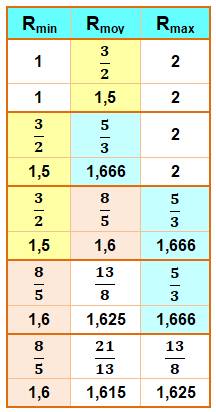
Propriété Le rapport entre deux nombres de Fibonacci successifs tend vers le
nombre d'or lorsque ces nombres tendent vers l'infini.
Explications Prenons trois nombres de Fibonacci successifs
comme 3, 5 et 8 et leurs deux rapports: 5/3 = 1,666… et 8/5 = 1,6. Ces deux rapports sont décroissants et cette
propriété est valable pour la suite de Fibonacci. On a ainsi deux rapports tels que a/b < c/d. Dans ce cas, on sait trouver une fraction médiane:
Convergence Progressivement, la fraction médiane est enfermée
dans un intervalle qui se réduit. Elle converge vers 1, 618 …, le nombre
d'or. Le tableau montre (code couleur) la naissance et
la destinée de chacun des rapports. Une fraction naissante (au centre)
devient soit la plus petite des deux lignes suivantes ou la plus grande. |
|
|||
|
Brèves associées |
>>>
Les
nombre k-bonacci |
>>>
Brèves Suites – Index |
||
|
Pour en savoir plus |
>>>
Fibonacci et nombre d'or |
>>>
Fraction médiane |
||
624. Racine carrée de puissances |
|
|||
|
Résultat peu intuitif pour ce calcul de la racine
d'un nombre à une puissance. En fait, la racine carrée est équivalente à une
puissance 1/2. Il suffit donc de diviser l'exposant par 2. |
|
|||
|
Brèves associées |
>>>
Puissances
négatives |
>>>
Brèves Puissances – Index |
||
|
Pour en savoir plus |
>>>
Puissances fractionnaires |
>>>
Puissances – Index |
||
625. Nombre plastique (Padovan) |
|
|||
|
Une constante qui est l'unique racine réelle de
cette équation du troisième degré. Cousin du nombre d'or. Rapport de convergence de
la suite de Padovan cousine de la suite de Fibonacci. |
= 1,324717957244746026… |
|||
|
Brèves associées |
>>>
Nombres d'or
et d'argent |
>>>
Brèves Types de nombres – Index |
||
|
Pour en savoir plus |
>>>
Nombres plastiques |
>>>
Suite de Fibonacci et nombre d'or |
||
626. Nombre d'ACHILLE |
|
|||
|
Nombres d’Achille Comme le héros
mythologique Achille, ces nombres sont puissants, mais pas puissance
parfaite. Nombre dont deux
facteurs au moins ont des exposants différents supérieurs à 1. Un nombre
puissant (ou plénipotent), non puissance parfaite, est un nombre d’Achille. |
Nombres d'Achille – Deux exemples
Puissants parfaits, mais pas
Achille 36 = 22
x 32 = 62 216 = 23 x 33 = 63
|
|||
|
Brèves associées |
>>>
Nombres
carrés |
>>>
Brèves Types de nombres – Index |
||
|
Pour en savoir plus |
>>>
Nombres d'Achille >>>
Nombres puissants |
>>>
Puissance parfaite >>>
Facteurs des nombres |
||
627. Calcul avec radicaux |
|
|||
|
But Résoudre cette équation avec des 1/2 et
l'inconnue en exposant. Possible ? Commentaires du tableau de
résolution D'abord les quatre fois 1/2 font 2. Cette écriture
est présente pour un simple effet esthétique. Tout comme la puissance 1/2 qui
est en fait une autre manière de noter la racine carrée. En remplaçant 16 par 24 , on met en
évidence un 2 à une puissance de chaque côté. Même si l'égalité semble évidente, passons par
les logarithmes pour confirmer. L'exposant 'une puissance devient un
coefficient. En divisant par ln(2), non nul, on retrouve bien ce qui semblait
évident. Une élévation au carré termine le calcul en
révélant que x = 16. |
Résolution de l'équation
En effet:
Seul cas de k puissance racine de x = x (sauf cas trivial
avec 1)
|
|||
|
Brèves associées |
>>>
Racine cubique – Deux chiffres |
>>>
Brèves Calculs – Index |
||
|
Pour en savoir plus |
>>>
Racines carrées |
>>>
Équations |
||
628. Équation en racine cubique |
|
|||
|
But Résoudre cette équation avec ces deux racines
cubiques bien encombrantes. Commentaires du tableau de
résolution S'il s'agit d'un exercice scolaire, il y a une
grande probabilité que l'expression sous radical soit un cube. Sinon la
résolution est particulièrement ardue. On cherche les coefficients d'un expression telle
que:
On note que a3 ne peut pas dépasser 6,
soit a = 1. On essaie b = 1 et ça marche ! |
Résolution de l'équation
|
|||
|
Brèves associées |
>>>
Racine cubique – Calcul mental |
>>> Brèves
Calculs – Index |
||
|
Pour en savoir plus |
>>>
Équations avec racines cubiques |
>>>
Racines continues |
||
629. Carré et deux cercles |
|
|||
|
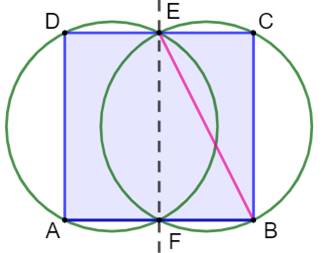
Problème Quel est le côté du plus grand carré recouvert
entièrement par deux cercles de rayon unité. Solution Le cercle 1 passe par A et D. Le cercle 2 passe par B et C. Les deux cercles sont interchangeables. La figure
est symétrique. Les deux cercles passent par E et F, les milieux de AB et DC. Dans le triangle rectangle BCE inscrit dans le
cercle, BE est un diamètre. Avec le théorème de Pythagore:
|
Carré le plus grand couvert par
deux cercles identiques de rayon R. Son côté vaut 1,78 R.
|
|||
|
Brèves associées |
>>>
Carré et
deux triangles équilatéraux |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Carré max couvert par k cercles |
>>>
Cercles – Index |
||
630. Carrés et quatre cercles |
|
|||||||||||||||||||||
|
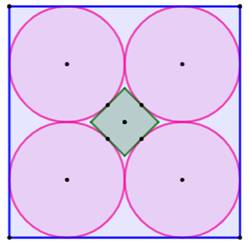
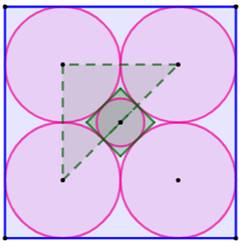
Problème Quelle est la longueur du côté du petit carré
vert ? C'est aussi le diamètre du cercle interne,
tangent aux quatre cercles. Solution Avec C = côté
du grand carré et c pour le petit. La figure de droite, avec le triangle isocèle
rectangle en vert, montre que:
|
|
|||||||||||||||||||||
|
Brèves associées |
>>>
Carré divisé – Aire manquante |
>>>
Brèves Géométrie – Index |
||||||||||||||||||||
|
Pour en savoir plus |
>>>
Sangakus |
>>>
Carrés – Index |
||||||||||||||||||||
631. Périmètre inconnu |
|
||||||||||||||||||||||||||||||||
|
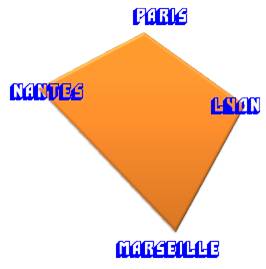
Énigme Quatre villes. Curieusement, on connait les
distances:
Quelle est la distance pour faire le tour complet
? Solution (p = Paris-Lyon, l =
Lyon-Paris, …) La somme des quatre trajets proposés correspond à
trois fois le tour complet comme le montre
ce tableau.
|
Plan
Bonus: calcul des distances entre
villes Quatre équations pour quatre inconnues: il est
possible de retrouver la distance entre villes (distances réelles). p = 381, l =
314, m = 985 et n = 384. |
||||||||||||||||||||||||||||||||
|
Brèves associées |
>>>
Entier manquant – moyenne |
>>>
Brèves Compter – Index |
|||||||||||||||||||||||||||||||
|
Pour en savoir plus |
>>>
Périmètre |
>>>
Énigmes – Index |
|||||||||||||||||||||||||||||||
632. Sous-ensembles de [1,2,3,4] |
|
|||
|
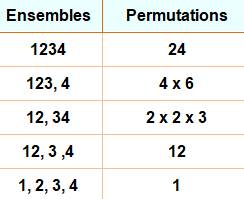
Il existe 73 façons de créer des sous-ensembles
ordonnés de l'ensemble [1, 2, 3, 4] .
|
73
sous-ensembles ordonnés avec
[1, 2, 3, 4]
Il en 501 pour
[1, 2, 3, 4, 5]. |
|||
|
Brèves associées |
>>>
Triangle
de Pascal – Propriétés |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Sous-ensembles ordonnés |
>>>
Compter les nombres |
||
633. Théorème du face à face |
|
|||
|
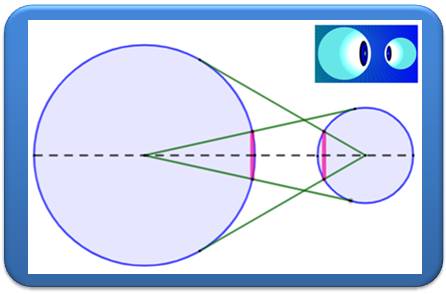
Deux
cercles quelconques (bleus). Les tangentes issues du centre des cercles
(vertes). Les
cordes (roses) sont égales. Le
quadrilatère ayant ces cordes pour côtés est un rectangle. La figure ressemble à deux yeux qui se font face.
D'où le nom en anglais: eyeball theorem,
pour théorème des globes oculaires ou théorème des quinquets. |
|
|||
|
Brèves associées |
>>>
Théorème
de Ptolémée |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Théorème du face à face |
>>>
Cercles – Index |
||
634. Nombres de Kaprekar |
|
||||||||
|
Définition Un nombre
de Kaprekar de n chiffres est tel que les chiffres de sa puissance k peuvent être partagés en k nombres
de n chiffres, et la somme de ces nombres est égale au nombre initial. Exemples
|
Multi-Kaprekar (rare) Le nombre 45 est Kaprekar d'ordre 2, 3 et 4:
Tous les repdigits en 9 sont Kaprekar
d'ordre 2.
|
||||||||
|
Brèves associées |
>>>
Cycle de
Kaprekar |
>>>
Brèves Itérations – Index |
|||||||
|
Pour en savoir plus |
>>>
Nombres de Kaprekar >>>
Nombres de Kaprekar – Tables |
>>>
Nombre 45 >>> Nombre 99 |
|||||||
635. Nombre 39 |
|
|||
|
Le nombre 39 est
égal au produit de ses chiffres ajouté à la somme de ses chiffres,
comme tous les nombres à deux chiffres terminés par 9.
Propriété évidente en décomposant:
|
Le nombre 39 et son penchant pour
le nombre 3
La barre au-dessus des nombres indique que ces
nombres sont concaténés. |
|||
|
Brèves associées |
>>>
Nombre 37 |
>>>
Brèves Nombres – Index |
||
|
Pour en savoir plus |
>>>
Nombre 39 dans le DicoNombre >>>
Nombres somme-produit |
>>>
DicoNombre |
||
636. Compter les chiffres |
|
|||
|
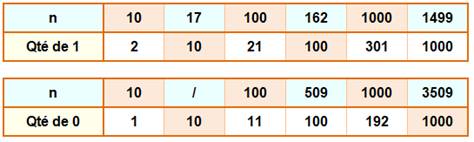
Comment lire le tableau Il y a, par exemple, 21 fois le chiffre 1 pour écrire tous les
nombres de 1 à 100. Un livre de 162 pages utilise 100 fois le chiffre
1 pour sa pagination. |
Jusqu'à 10, il y a les nombres 1 et 10, ce qui
totalise deux fois le 1; et, une seule fois le 0. Pour écrire 10 fois le 1,
il faut tous les nombres de 1 à 17.
|
|||
|
Brèves associées |
>>>
Anagramme
des nombres |
>>>
Brèves Compter – Index |
||
|
Pour en savoir plus |
>>> Compter
les chiffres jusqu'à n |
>>>
Chiffres – Index |
||
637. Puissance des puissances de 2 |
|
|||
|
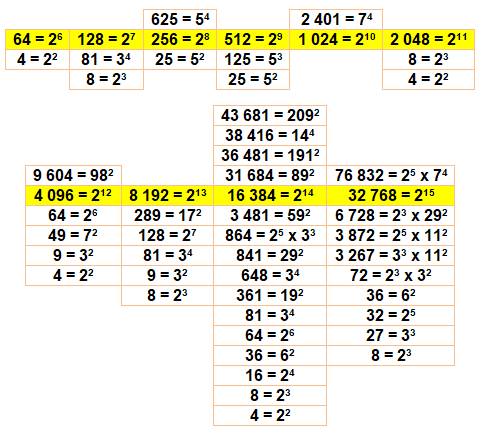
Formation des puissances Amusement avec les chiffres des puissances de 2. Quelles sont les autres puissances que l'on peut
former avec ces chiffres. Exemple Le bicarré de 7 est formé des mêmes chiffres que la
puissance dixième de 2.
On peut former 16 ( = 24) puissances
avec les chiffres de 214. |
|
|||
|
Brèves associées |
>>>
Somme de
puissances |
>>>
Brèves Puissances – Index |
||
|
Pour en savoir plus |
>>>
Chiffres des puissances de 2 |
>>>
Puissances de 2 |
||
638. Pourquoi: 0,999… = 1 |
|
|||||||||||||||||||||||||||
|
Une affaire d'infini Ayant un nombre décimal comme 0,111, il est
toujours possible de trouver un nombre plus grand comme 0,112, ou même
beaucoup comme 0,1111 ou 0,11111111. Non, ce n'est pas toujours possible ! Prenez le nombre 0,999, alors 0,99999999 est plus
grand. D'accord ! Mais s'il y a une infinité de 9, on a: 0, 9999 … (infinité). Et là, impossible d'y loger
une 9 supplémentaire. Bien obligé de passer à 1. Dit-autrement, il n'y a aucun nombre entre 0,999… et 1, c'est donc que
ces deux nombres sont deux écritures différentes du même nombre. |
Constat 1
Constat 2
|
|||||||||||||||||||||||||||
|
Brèves associées |
>>>
Nombre
0,0097… = 1/103 |
>>>
Brèves Nombres – Index |
||||||||||||||||||||||||||
|
Pour en savoir plus |
>>>
Nombre 0,999… = 1 |
>>>
Nombre 0,999… >>>
Nombre 1 |
||||||||||||||||||||||||||
639. Quantité de premiers |
|
|||
|
Compter les nombres premiers La fonction Pi(n) indique quelle est la quantité
de nombre premiers inférieure à n, ce nombre compris. Ainsi, en comptant les nombres premiers jusqu'à
10, on trouve: 2, 3, 5, 7 et P1(10) vaut
4. Il est possible de les compter rigoureusement
jusqu'à une certaine limite. Ensuite, la quantité est estimée avec Pi(n)
proche de n / ln(n). Curiosité unique
|
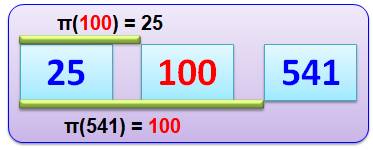
Exemple avec le nombre 100
100 est le vingt-cinquième nombre premier, et 541 est le centième. |
|||
|
Brèves associées |
>>>
Nombre
0,0097… = 1/103 |
>>>
Brèves Premiers – Index |
||
|
Pour en savoir plus |
>>>
Quantité de nombres premiers |
>>>
Nombre 100 |
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()