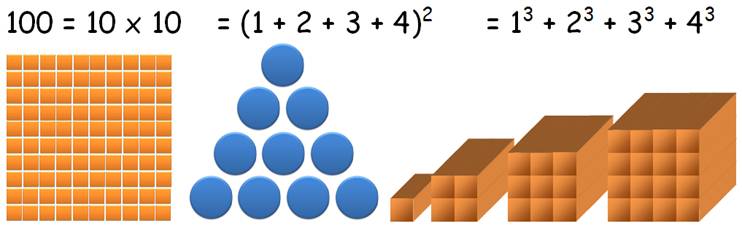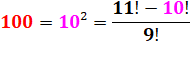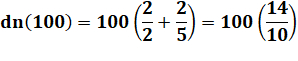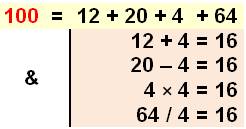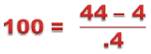Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 06/11/2024 M'écrire Brèves de Maths

Débutant Glossaire Types de nombres Nombres géométriques Nom des nombres Écriture des nombres Table des facteurs Nombres et anglais Langues	Dictionnaire des Nombres
	1 / 10 / 50 / 60 / 70 / 75 / 76 / 77 / 78 / 79 / 80 / 81 / 82 / 83 / 84 / 85 / 86 / 87 / 88 / 89 / 90 / 91 / 92 / 93 / 94 / 95 / 96 / 97 / 98 / 99	100	101 / 102 /103 / 104 / 105 / 106 / 107 / 108 / 109 / 110 / 115 / 120 / 130 / 140 / 150 / 200 / 250 / 300 / 400 / 500 / 1000 / Autres

CENT	Linguistique 100	Maths	Jeux avec 100
Culture 100 (1/2)	Expression 100	Sciences 100	Curiosités
Culture 100 (2/2)	Proverbes 100	Économie 100	Quizz 100
Pluriels détournés

Cent

One hundred

Orthographe / Langues

Facteurs
Diviseurs	1, 2, 4, 5, 10, 20, 25, 50, 100
Quantité	9
Somme	217
Binaire	110 0100
Romain	C

Suite en identité détaillée

100 = C en romain, ce qui place ce nombre en premier par ordre alphabétique en romain.

Abondant

Auto-descriptif

Auto-évitant

Composé

Dihédral

Harshad

Harshad à Q-carré

Harshad trivial

Hecto

Heureux

Holopotentiel

Leyland

Pair,

Pratique

Puissant

Puissance de dix

Semi-parfait

Géométrique

2-pentagonal (8^e)

Carré

Nombre figuré d'ordre 18

Nombre triangulaire au carré et somme de cubes

Configuration remarquable avec 100

Voir Propriété générale des cubes

Voir Pépites / Tétraktys / Holopotentiel

Particularités

Le produit de ses diviseurs: 1 000 000 000

La partition la plus généreuse: 100 = 3x32 + 2x2 => 3³² x 2² = 7 412 080 755 407 364

La somme des diviseurs vaut 2n + 17. Cas unique avec 17.

Voir Analyse des diviseurs de 100 / Partitions généreuses

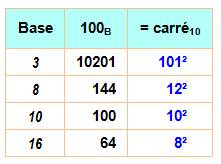
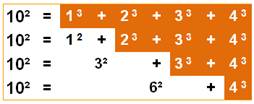
Curiosité: 100 et ses carrés

Le nombre 100 exprimé en certaines bases est aussi un nombre décimal au carré.

Numération

de 0 à 100 => 193 chiffres	Il y a 190 chiffres pour écrire les nombres de 0 à 99 et trois de plus pour aller à 100. Il en faut 2890 pour aller jusqu'à 999. C'est 38 890 pour 9 999 et 488 890 pour 99 999. Etc.
100 = 10²			100 vaut 10 x 10 quelle que soit la base. Normal! En numération de position, le poids suivant est le carré du précédent.
1010 = 10102 10010 = 11001002 100010 = 11111010002		Le binaire contient le nombre. Vrai pour toutes les puissances de 10.

Multiplication

100 = 2² x 5² = 10²

Voir Carte d'identité du nombre 100. Voir Analyse des diviseurs

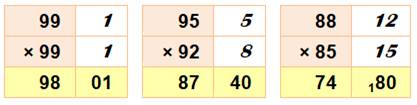
Multiplications rapides de nombres proches de 100

Complément à 100 à droite u et v; Produit u.v pour dizaines et unités; Somme u + v retirée des milliers et centaines.

Voir Suite avec autres cas autour de 100, et autres multiplications rapides

100 = 2 x 2 x 5 x 5 = 2 x 2 x 25 = 4 x 5 x 5 = 2 x 5 x 10 = 2 x 50 = 4 x 25 = 5 x 20 = 10 x 10	Huit multiplications pour donner 100 (hors usage du 1, bien entendu).
100 = 1x2 + 3x4 + 5x6 + 7x8	Somme de produit des nombres successifs.
100 = (5 – 1) (5 – 0) (5 – 0)	Nombre complémenté à 5.
100 / (1 + 0 + 0) = 100	Nombre de Harshad, comme toutes les puissances de10.
100 = (5 + 5) (5 + 5) = 99 + 9/9	Jeu: écrire 100 avec quatre fois le même chiffre.

Division

Recherche des facteurs des nombres de 100 à 112

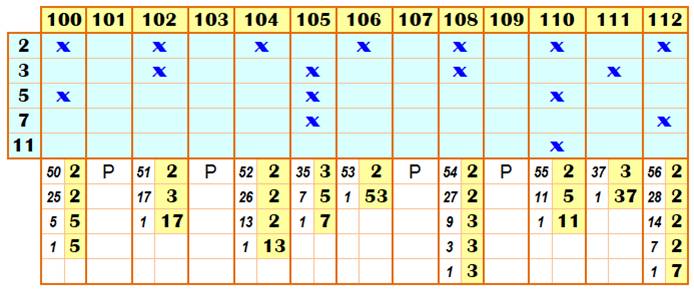
Voir Crible d'Ératosthène

100 = 50 + 25 + 20 + 5	Nombre semi-parfait: somme d'un sous-ensemble de ses diviseurs.
	Carré = cette relation entre factorielles successives.
100 = tau (45 360)	Quantité de diviseurs de 45 360, nombre hautement composé. Quantité de diviseurs du nombre un milliard.
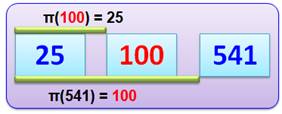
		Fonction Pi(n): quantité de nombres premiers jusqu'à n compris. 100 est le vingt-cinquième nombre premier, et 541 est le centième.
Il y a 25 nombres premiers inférieurs à 100 et, 100 est multiple de 25.		Nombre MulQprem.
Phi(100) = 40	Phi est le totient d'Euler: il y a 40 nombres plus petits que 100 et premiers avec 100. Ce sont (en rose, nombres composés): 1, 3, 7, 9, 11, 13, 17, 19, 21, 23, 27, 29, 31, 33, 37, 39, 41, 43, 47, 49, 51, 53, 57, 59, 61, 63, 67, 69, 71, 73, 77, 79, 81, 83, 87, 89, 91, 93, 97, 99.

Addition: partition en entiers

p(100) = 190 569 292 – toutes 1 116 – en carrés 39 – en cubes 9 – en puissances 4 444 793 – distinctes	Quantité de partitions du nombre 100. Oui ! il existe un peu plus de 190 millions de façons d'écrire une addition dont la somme vaut 100.
100 = 10 + 20 + 30 + 40 = 10 (1 + 2 + 3 + 4)	Pendant de 10 = 1 + 2 + 3 + 4.
100 = 18 + 19 + 20 + 21 + 22 = 9 + 10 + … + 16 (8 termes)	Seules sommes de k nombres consécutifs positifs >>> Nombre 2-pentagonal: somme des huit nombres supérieurs à 8.
100 = 1 + 2 +…+ (1 + 8) + (1 + 9)	Somme des chiffres des nombres de 1 à 19.
100 = 2 + 19 + 79 = 2 + 31 + 67 = 2 + 37 + 61	Trois fois somme de trois nombres premiers. Le nombre 100 est pair ce qui implique la présence du 2.
100 = 2 + 3 + 5 + 7 + 11 + 13 + 17 + 19 + 23	Somme des neuf plus petits nombres premiers. Première telle somme en tant que carré. Le carré suivant n'est obtenu que pour la somme des 2 474^e premiers nombres premiers. Les sommes divisibles par 100 pour p = 23, 563, 937, 2099, 3371, 5407, 6977 …
100 = 1 + 3 + 5 … + 19 = 10² et 19 = 2 x 10 – 1	Somme de 10 impairs successifs. Tous les carrés possèdent cette propriété: somme des impairs consécutifs.
100 = 2 + 6 + 7 + 8 + 21 + 56 & 1/2 + 1/6 + 1/7 + 1/8 + 1/21 + 1/56 = 1	Nombre bon. Il existe 137 partitions de 100 telles que la somme des inverses donne 1. Trois sommes ont des termes uniques.
100 = 8 + 14 + 20 + 26 + 32	Somme de nombres en progression arithmétique de raison 6.
	Une partition singulière du nombre 100 et relation de chaque terme avec les quatre opérations et le nombre 4.
100 = 3 + 97 = 11 + 89 = 17 + 83 = 29 + 71 = 41 + 59 = 47 + 53	Six fois somme de deux nombres premiers.
100 = 18 + 19 + 20 + 21 + 22 = 9 + 10 + … + 15 + 16	Somme de cinq et huit nombres consécutifs.
100 + 101 + … + 110 = 111 + … + 120	Somme de nombres consécutifs. Propriété de tous les carrés.
100 = 15 + 21 + 28 + 36 = 45 + 55 = T5 + T6 + T7 + T8 = T9 + T10	Double somme de nombres triangulaires.
100 = 47 + 53 100 = 41 + 59 100 = 29 + 71 100 = 17 + 83 100 = 11 + 89 100 = 3 + 97	Nombre présentant 198 partitions en somme de nombres premiers distincts, dont voici les 6 présentations à deux termes.
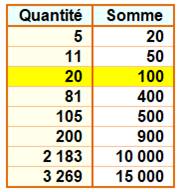
3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5, 8, 9, 7, 9, 3, 2, 3, 8, 4, 6	Somme des 20 premières décimales de pi Le tableau présente la quantité nécessaire de décimales pour atteindre la somme indiquée
100 = 20 +40 +40 = 10² et 20² + 40² + 40² = 60² = 3 600	Somme carrée dont la somme des carrés des termes est aussi un carré.
100 = P13 (hors partition par lui-même)	Les cent partitions propres du nombre 13.
100 = (25+1) + (25-1) + (25x1) + (25/1) = (16+4) + (16-4) + (16x4) + (16/4) = (9+9) + (9-9) + (9x9) + (9/9)	Somme des quatre opérations, trois fois. Forme en 9, typique des carrés.
100 = 2+7+9+…+5 et 27 969 886 988 875 = 30 355^3 100 = 1+0+9+…+1 et 1 099 988 928 898 561 = 5 759^4 100 = 4+9+6+…+8 et 4 968 737 893 838 368 = 1 378^5 100 = 9+5+9+…+1 et 9 598 548 249 896 761 = 461^6	Sommes des chiffres d'une puissance de 3, 4, 5 et 6 Motif qui n'existe pas pour les puissances 2 et 7.

100 [1, 2, 3, 5, 13, 21, 55] [1, 2, 8, 13, 21, 55] [3, 8, 13, 21, 55] [1, 2, 3, 5, 34, 55] [1, 2, 8, 34, 55] [3, 8, 34, 55] [1, 2, 3, 5, 89] [1, 2, 8, 89] [3, 8, 89]

Représentation de Zeckendorf du nombre 100. Pour le nombre 100, il existe neuf sommes faites avec des nombres de Fibonacci distincts. En rouge, les nombres de Fibonacci consécutifs. La dernière (100 = 3 + 8 + 89) est constituée de nombres de Fibonacci distincts et non consécutifs, c'est la représentation de Zeckendorf. Elle est unique pour tous les nombres. Notation binaire de cette somme de Zeckendorf

Partition en carrés

Petite énigme (calcul simple)

n est la quantité de chiffres répétés

Voir Brève 50-991

Autres seuls cas

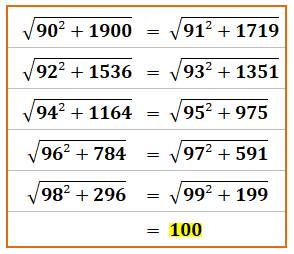
100² = 99 x 101 + 1 = 9 999 + 1

Principe de calcul mental des carrés.

100

Longueur de la période de répétition des trois derniers chiffres d'un carré.

100 = 9 + 10 + … + 16

= 18 + 19 + 20 + 21 + 22 = 5 x 20

Deux seules sommes de nombres consécutifs >>>

Calcul mental facile avec la somme en 20.

n = 100

101² – 99² = 400

102² – 98² = 800

103² – 97² = 1200

Progression de la différence de carrés de nombres autour de 100.
Propriété générale des nombres en 4n.

100 = 10² = 6² + 8² = 36 + 64

= 7² + 5² + 5² + 1²

= 7² + 5² + 4² + 3² + 1²

= 7² + 4² + 7(2² + 1²)
= 6² + 4² + 4² + 4² + 4² = 6² + 4³
= 6² + 5² + 4² + 3² + 3² + 2² + 1²

= 6² + 5² + 5² + 3² + 2² + 1²

= 6² + 6² + 4² + 2² + 2² + 2²

= 5² + 5² + 4² + 4² + 3² + 3²

= 5² + 4² + 4² + 4² + 3² + 3² + 3²

Nombre binomial.

Nombre carré somme de deux carrés.

Et nombreuses somme de carrés.

Autres sommes de carrés >>>

100 = 5² + 5² + 5² + 5²

Somme de carrés de nombres premiers.

100 = 1² + 1² + 7² + 7²

= 1² + 3² + 3² + 9²

= 1² + 5² + 5² + 7²

= 2² + 4² + 4² + 8²

= 5² + 5² + 5² + 5²

Carré somme cinq fois de quatre carrés

100 = 6² + 8² = 6² + 2⁶ = 64 + 36

Nombre de Leyland
Forme sympathique en 2 et 6

100 = (10² + 0²)

= ( 6² + 8²)

= (1² + 1²) (1² + 7²)

= (1² + 1²) (5² + 5²)

= (1² + 2²) (2² + 4²)

= (1² + 3²) (1² + 3²)

= 7² + 7² + 1² + 1²

= 5² + 5² + 5² + 5²

= 8² + 4² + 4² + 2²

= 9² + 3² + 3² + 1²

Somme de carrés, produit de somme de carrés.

Nombre de Brahmagupta.

4 fois produit de somme de deux carrés.

4 fois somme de quatre carrés.

100 = 1 x 5² + 3 x 5²

= 1 x 6² + 4 x 4²

= 1 x 8² + 4 x 3²

= 1 x 8² + 1 x 6²

= 2 x 1² + 2 x 7²

= 4 x 1² + 6 x 4²

= 4 x 4² + 9 x 2²

= …

Autour des triplets de Pythagore.

Carrés et autres puissances.

100	=	2	x	50
6² + 8²		1² + 1²		1² + 7²
100	=	5	x	20
10² + 0²		1² + 2²		2² + 4²

Deux fois: somme de 2 carrés et produit de deux nombres eux-mêmes somme de 2 carrés. La liste est : 4 10 16 20 25 26 34 36 40 50 … Identité de Lagrange

100 = 10² – 0²

= 26² – 24² = 676 – 576

Deux seules différences de carrés pour 100 avec termes inférieurs à 100.

100² = 145² – 105²

10 000 = 21 025 – 11025

Carré = Pentagonal – Triangulaire

Plus grand cas de différence de carrés (ou triplet de Pythagore) avec ce motif géométrique. Le seul autre triplet avec cette propriétés: (3, 4, 5).

J.-M. De Koninck / R.K. Guy

(100 + 1)² – (100 – 1)²

= (100 1) (100 + 1) = 2 x 200

= 101² – 99² = 20²

Triplet de Pythagore autour de 100.

Partition en cubes et autres puissances

100 = 1^3 + 2^3 + 3^3 + 4^3 = 1 + 8 + 27 + 64 = (1 + 2 + 3 + 4) ² = (10) ²	Nombre holopotentiel Somme des cubes des nombres consécutifs = carré de la somme de nombres. Propriété générale: 10 (= 1 + 2 + 3 + 4) est un nombre triangulaire. Le carré 100 est alors somme de cubes. Cycle narcissique de sommes de cubes.
100 = 1^3 + 2^3 + 3^3 + 4^3 = 20 x 5	Somme de puissances de nombres consécutifs divisible par le nombre suivant. Propriété générale.
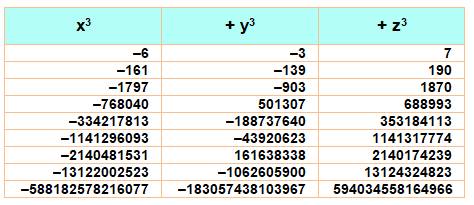
100 = x^3 + y^3 + z^3 = (–6)^3 + (–3)^3 + 7^3 = 343 – 216 – 27		Partition du nombre 100 en sommes de cubes. Solutions du problème de la somme de trois cubes illustrant que dans certains cas les solutions sont nombreuses (infinies?).
100 = 7^3 – 6^3 – 3^3 = 343 – 216 – 27	Somme de trois cubes.
100 = 5^3 – 5^2 500 = 5^4 – 5^3	Différence de puissances d'un même nombre. Seule solution réelle de x^3 – x^2 = 100. Différence de puissances de 5.
100 = 2² (2^4 + 3²) = 4 (16 + 9)	Motif en 2, 3 et 4
100 = 6^2 + 2^6	Nombre de Leyland: nombre en a^b + b^a
100 =	Curiosité de calcul.

Autour du nombre

–100 = (5 + i5)^4 = (5 – i5)^4	Entier = puissance de nombre complexe.
100! = 9,33… 10^157 = 933…000…00024 = 2^97 x 3^48 x 5^24 x 7^16 x 11^9 x 13^7 x 17^5 x 19^5 x 23^4 x 29^3 x 31^3 x 37^2 x 41^2 x 43^2 x 47^2 x 53 x 59 x 61 x 67 x 71 x 73 x 79 x 83 x 89 x 97		Factorielle 100, nombre qui comporte 24 zéros finaux.
10^100	Gogol : un 1 suivis de cent 0.

Jeux et curiosités

Cent		Le premier nombre de la liste alphabétique de tous les nombres écrits en lettres.
10010 = 12104		Le plus petit nombre auto-descriptif en base décimale, car en base 4, on a: Le 1 indique qu'il y a un seul 0 dans ce nombre; Le 2 indique qu'il y a deux 1; Le 1 suivant signifie que le nombre contient un seul 2; et Le 0 final témoigne de la non-présence du 3.
100n = n		Le nombre n au carré, exprimé dans la base n, s'écrit 100.
1 + 2 + 3 … + 100 = 5 050		Calcul de la somme de 1 à 100.
100	Quantité de produits distincts de trois nombres de 1 à 9. Ce sont: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 24, 25, 27, 28, 30, 32, 35, 36, 40, 42, 45, 48, 49, 50, 54, 56, 60, 63, 64, 70, 72, 75, 80, 81, 84, 90, 96, 98, 100, 105, 108, 112, 120, 125, 126, 128, 135, 140, 144, 147, 150, 160, 162, 168, 175, 180, 189, 192, 196, 200, 210, 216, 224, 225, 240, 243, 245, 252, 256, 270, 280, 288, 294, 315, 320, 324, 336, 343, 360, 378, 384, 392, 405, 432, 441, 448, 486, 504, 512, 567, 576, 648, 729.

Les deux jeux les plus classiques pour atteindre 100 avec des calculs

100 = 123 – 45 – 67 + 89	Utilisation de tous les chiffres. – Voir Autres solutions.
	Il existe onze telles fractions pannumériques égale à 100.

	Comment faire 100 avec k fois le même chiffre. À droite, solution avec notation anglaise (.4 = 0,4) – Voir le tableau des solutions des sommes à cinq termes pour tous les chiffres. Aussi, tableau pour k termes. – Voir cas particulier du jeu du quatre 4.
100 = 111 – 11 100 = 33 × 3 + 3/3 100 = 5 × 5 × 5 – 5 × 5 100 = (666 – 66 ) / 6 100 = (7 + 1/7) (7 + 7) 100 = 99 + 9/9

100 = 10 + 23 + 27 + 40	Jeu: Trouver la somme 100.
100 = 81 + 19	Jeu: Avec ces mêmes chiffres faire 79.
Théorème 100: Ce théorème est le dernier de ce livre. Preuve: Évidente.	Énoncé par John Conway dans un de ses livres: Nombres et Jeux.
100 et somme cachée	Deviner la somme.
100 = x^3 + y^3 + z^3 + w^3 …	Système d'équations à résoudre.
100 et 8	Tableau liant les nombres 100 et 8
100 m² = 1 are	Unités se surface.

100,530 964 914 …

Aire du demi-cercle de rayon 8 >>>

Cardinalités

193	Quantité de chiffres pour écrire tous les nombres de 0 à 100.
5 050 5 050² = 25 502 500	Somme des nombres de 1 à 100 = ½ 100x 101. C'est le 100^ème nombre triangulaire. Somme des cubes des nombre de 1 à 100
338 350	Somme des carrés des nombres de 1 à 100
7 51 354 224 848 179 261 915 075	Le 100^ème chiffre de Pi et de e. Le 100^ème nombre premier Le 100^ème nombre de Fibonacci
100 = 96 + 4	Nombres premiers seulement dont tous les chiffres vont croissants, comme le plus grand: 23 456 789; en comptant 2, 3, 5 et 7.
30 / 744	Quantité de partitions de 100 en trois / quatre carrés.
45 360	Plus petit nombre ayant 100 facteurs.
124 / 194	Seuls nombres dont la somme des diviseurs propres est 100. Aucun nombre ne totalise une somme de diviseurs égale à 100.
24 133	Ce nombre premier est la somme des cent plus petits nombres premiers.

Compléments

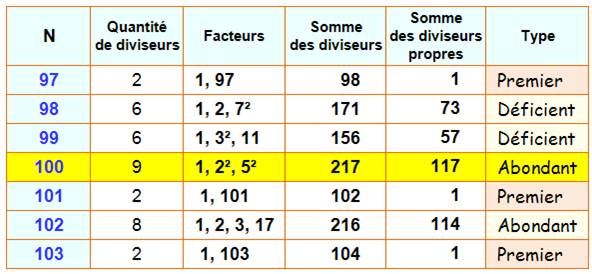
NOMBRES au voisinage de 100

Voir Premier, Déficient et abondant

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
100 2, [1, 1, 0, 0, 1, 0, 0] 3, [1, 0, 2, 0, 1] 4, [1, 2, 1, 0] 5, [4, 0, 0] 6, [2, 4, 4] 7, [2, 0, 2] 8, [1, 4, 4] 9, [1, 2, 1] 10, [1, 0, 0] 11, [9, 1]	12, [8, 4] 13, [7, 9] 14, [7, 2] 15, [6, 10] 16, [6, 4] 17, [5, 15] 18, [5, 10] 19, [5, 5] 20, [5, 0] 21, [4, 16]	22, [4, 12] 23, [4, 8] 24, [4, 4] 25, [4, 0] 26, [3, 22] 27, [3, 19] 28, [3, 16] 29, [3, 13] 30, [3, 10] 60, [1, 40]	19, [5, 5] 24, [4, 4] 49, [2, 2] 99, [1, 1]

Voir Bases / Brésiliens

Suite	Nombre 100 – Sciences Nombre 100 – Autres pages Nombre 101 Autres nombres
Voir	100 avec chiffres – Jeux Nombre Abondant Nombre Amiable Nombre de Kaprekar	Nombres Tétraédraux Palindrome Premier Circulaire
Références	Nombres par leur nom Empreinte des nombres DicoNombre Junior	Historique de ce site et Références Maitres en nombres
Site	Fun Facts About the Number 100 – Owlcation – TR Smith
Cette page	http://villemin.gerard.free.fr/NombDico/N100a500/Nb100Nb.htm