énigme du chou, de la chèvre et du loup

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/01/2023 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	JEUX
Débutants Général	Énigmes				Glossaire Général
INDEX Jeux	Filles	Chocolat	Chou Loup	Chèvres attachées
		Sommaire de cette page >>> Pour se lancer >>> Deux couples et leurs sacs (SIMPLE) >>> Loup, chèvre et chou (CLASSIQUE) >>> Formalisation >>> Variantes >>> Les couples (AUTRE EXEMPLE)

Problème de la traversée

du loup, de la chèvre et du chou

Énigme archi-classique de la traversé de la rivière avec des éléments incompatibles. Comment organiser les norias de sorte que tous les éléments d'un bord passe de l'autre côté sans dommage?

Il en existe de nombreuses variantes.

Historique: Alcuin (735-804); Chuquet (1445-1500); Tartaglia (1499-1557); Ozanam (1640-1717) ont chacun publié sur cette énigme.

Devinette

Il faut aller de l'autre côté de la rivière en passant sur un pont étroit ne pouvant supporter que deux personnes. Il fait nuit, alors l'un d'eux doit porter une torche unique.

A traverse en 1 minute;

B traverse en 2 minutes;

C traverse en 5 minutes;

D traverse en 8 minutes; et

Le plus lent fixant la vitesse, comment minimiser le temps de passage des quatre personnes ? Est-ce possible en 15 minutes ?

Solution

Pour se lancer …
Défi Six personnes et un tapis magique pour se rendre d'Angleterre en France. Pas plus de deux personnes à la fois sur le tapis. Chacun est sensible à la vitesse: ne pas dépasser 1, 3, 7, 9, 11 et 13 minutes pour le trajet selon les personnes. Durée minimum pour amener tout le monde en France ? Une solution évidente Cinq allers à deux et quatre retours avec un seul passager. C'est le plus rapide qui convoie les autres. 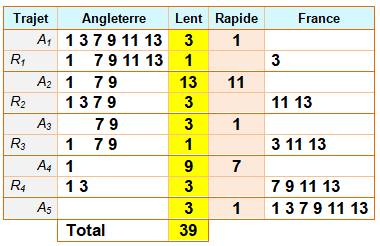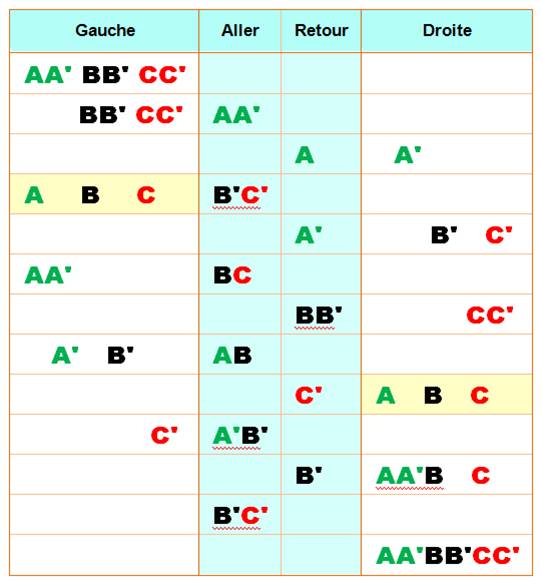Total: (1+3+7+9+11+13) + 4x1 = 48 minutes	Solution Il existe mieux que 48 minutes avec 39 minutes. Idée: faire passer les deux plus lents ensembles Ce tableau montre les allers-retours. Colonne jaune pour l'individu le plus lent. Colonne ocre pour le deuxième passager.
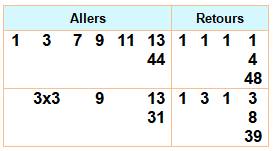
Comparaison Le tableau montre comment on n'a pas hésité à consommer un peu plus (8 au lieu de 4) durant les retours pour mieux minimiser les allers (31 au lieu de 44). Pour un solde positif de 9 minutes (39 au lieu de 48).

Proposé par Alex Bellos dans The Guardian du 10/08/2020

Caractérisation

Traversée de la rivière

Déplacement

Raisonnement

Classique

Primaire

Deux couples et leurs sacs – Simple

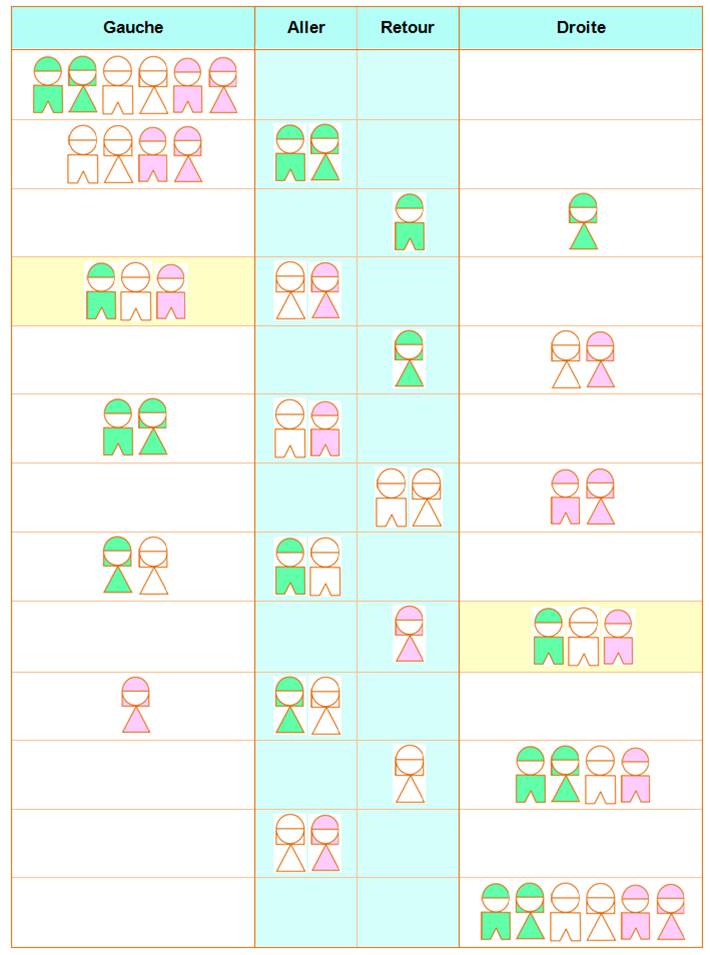
Énigme

Deux couples en randonnée face à une rivière.

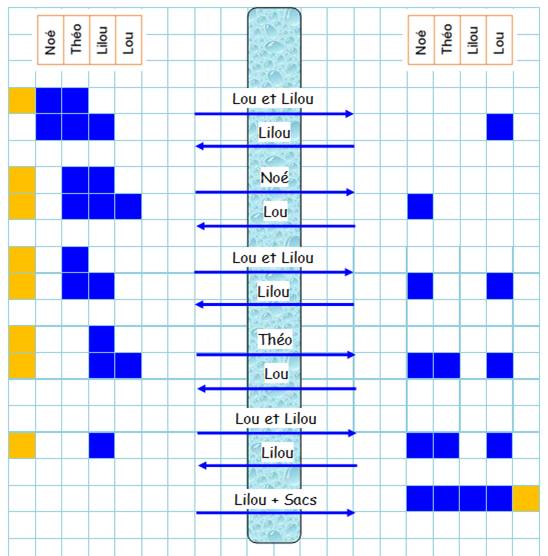
Chaque homme (Noé et Théo) pèse 80 kg et porte un sac de 20 kg

Chaque femme (Lou et Lilou) pèse 40 kg.

Le radeau supporte 80 kg, pas plus.

Comment traverser la rivière ?

Solution

Premier mouvement: les deux filles (Lou et Lilou) traversent (2 x 40 kg, ça passe). Lou reste sur l'autre rive et Lilou revient seule avec le radeau. Etc.

Voir Prénoms amusants

LOUP, CHÈVRE ET CHOU – Le Classique!
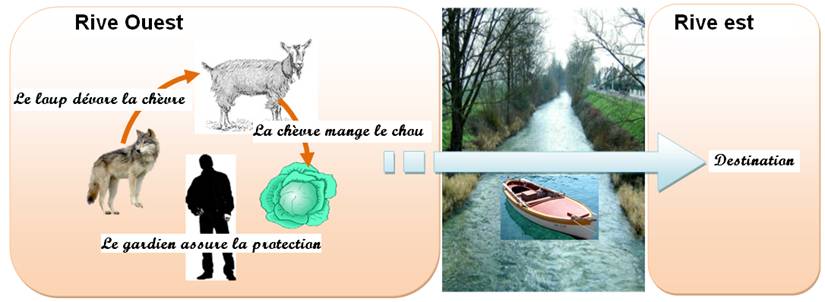
Il s'agit de faire traverser la rivière à des éléments dont certains sont incompatibles, car prédateurs l'un de l'autre. À moins que l'homme les surveille.	Le bateau peut transporter l'homme et un élément, mais pas plus. Comment s'y prendre? Et en combien de voyages ?
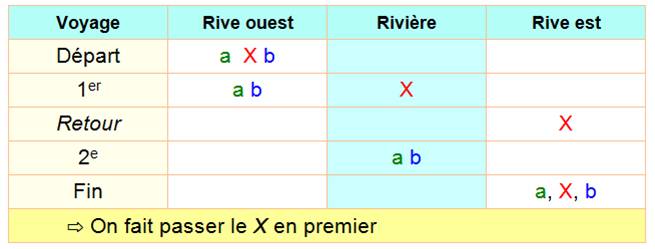
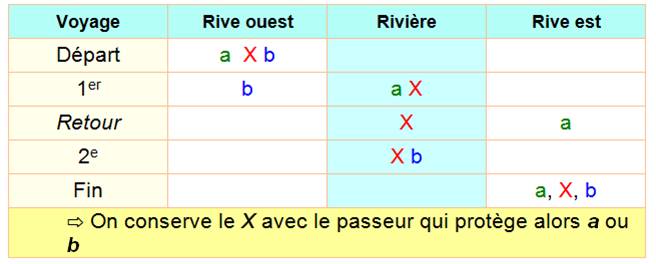
Remarque : la chèvre seule avec le chou, elle le mange; ou le loup, elle se fait dévorer.

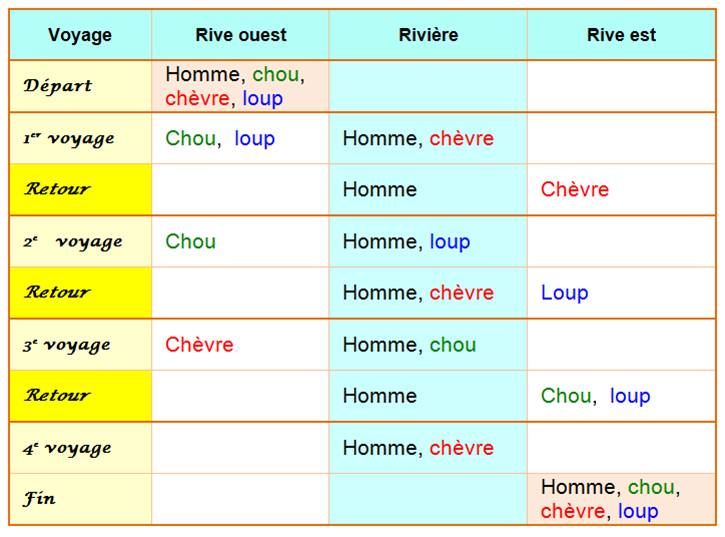
Solution

Tableau

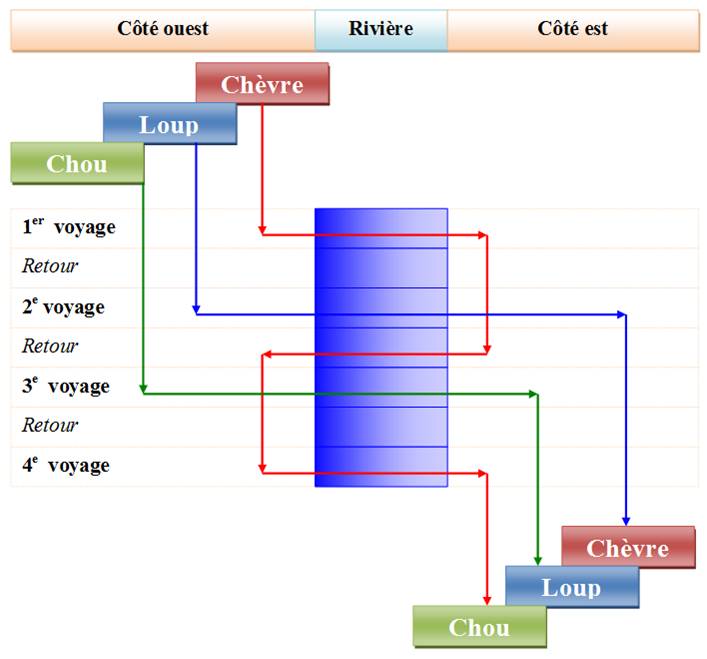
Graphique

Formalisation

Posons le problème

On ne peut pas laisser la chèvre en compagnie, car ou elle mange le chou ou elle se fait dévorer par le loup. Il existe donc, un élément (X) à ne pas laisser avec un des deux autres.

Par contre, les deux autres (a = loup et b = chou) sont compatibles.

On oublie l'homme qui intervient tout le temps. Cependant, n'oublions pas qu'il est le seul à permettre la cohabitation.

Énigme de base

Solution

X peut être seule, mais jamais avec a ou avec b.

Variantes – Passage à deux

Solution 1

Solution 2

Solution 3

Les couples – Un autre exemple

Trois couples sur la berge gauche veulent se rendent sur la berge droite.

Les hommes sont séducteurs: un homme ne doit jamais être avec une autre femme sans son mari.

La barque est dimensionnée pour deux, pas plus.

Nous avons M. et Mme VERT, M. et Mme BLANC et M. et Mme ROSE.

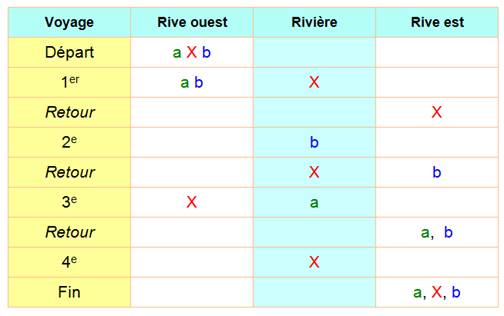
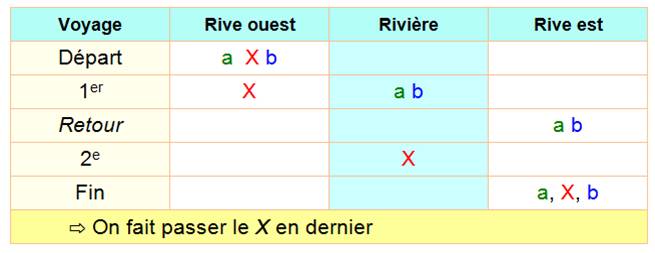
Des variantes sont possibles, mais toujours avec au moins six aller-retour.

Pour ceux qui préfèrent suivre avec des lettres:

Devinette – Solution

Énigme

Il faut aller de l'autre côté de la rivière en passant sur un pont étroit ne pouvant supporter que deux personnes. Il fait nuit, alors l'un d'eux doit porter une torche unique.

A traverse en 1 minute;

B traverse en 2 minutes;

C traverse en 5 minutes;

D traverse en 8 minutes; et

Le plus lent fixant la vitesse, comment minimiser le temps de passage des quatre personnes ? Est-ce possible en 15 minutes ?

Réponse

A et B traversent et A revient avec la torche (3 min).

C et D traversent et B revient avec la torche (10 min).

A et B traversent à nouveau (2min).

Total: 3 + 10 + 2 = 15 minutes.

Retour / Autres énigmes / Énigmes 2022