|
||||||||||||||||||||||||||||
![]()
|
Différences entre nombres = Carrés En
1682, Michel Rolle
résout le problème des quatre nombres proposé par Jacques Ozanam dans le
Journal des savants. Ozanam pensait le problème insoluble car nécessitant des
nombres de plus de 50 chiffres. Rolle trouve la solution avec des nombres à
sept chiffres. Approchons
ce problème en cherchant des configurations du même type. Quels sont les n
nombres dont les différences mutuelles sont des carrés? |
|
Peu de nombres sont
tels que n² - n se terminent par trois zéros:
376² – 376 = 141 000
625² – 625 = 390 000 9 376² – 9 376 = 87 900 000 |
Voir Carrés
qui se terminent par eux-mêmes
|
|
||
|
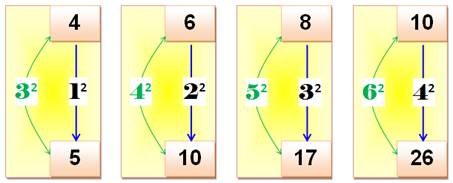
Problème Trouvez deux nombres a et b
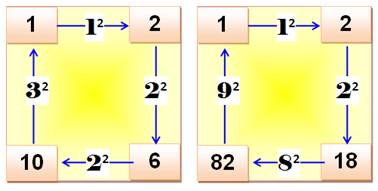
tels que: b – a = n² b + a = x² Le premier exemple ci-contre
donne: 5 + 4 = 9 = 3² 5 – 4 = 1 = 1² Propriété Notez le motif qui se répète:
Une manière particulière de
redécouvrir les identités
remarquables. |
Exemples
Explications a
= 2k = 2 x 2 b
= k² + 1 = 2² + 1 = 5 b
– a = k² -2k +1 = (k – 1)² b
+ a = k² + 2k + 1 = (k + 1)² Pour tout k, les deux nombres a = 2k et b = k² 1 ont une somme et une différence carrées. |
|
|
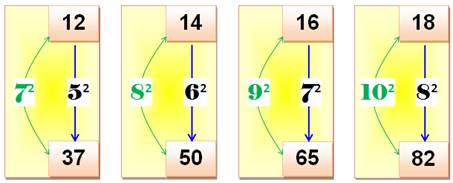
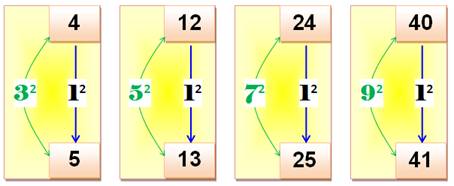
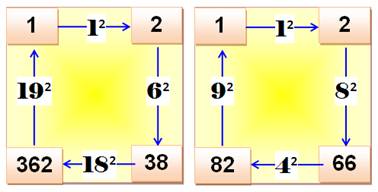
Il existe d'autres possibilités en conservant une
différence égale à 1. Le premier à gauche illustre
les cas où: a = k; b = a + 1² = k + 1 a + b = 2k + 1 =
x² qui se vérifie pour k = 4, 12, 24, 40, 60 … qui donne x = 3, 5,
7, 9, 11, 13 … En fait, pour tout x impair |
Pour tout x (somme des carrés) = 2k + 1, la somme et la différence de
a = k et b = k + 1 sont des carrés. |
|
|
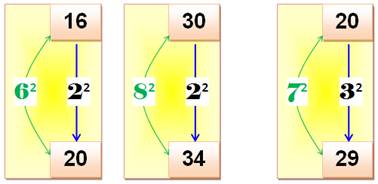
Différence égale à 2², 3² et plus Pour b – a = 2²: a = k; b = a + 2² a + b = 2(a + 2)
= x² Qui se vérifie pour a = 6, 16, 30, 42 … qui donne x = 4, 6, 8, 10 … On peut mener le même
raisonnement pour tous les carrés suivants. |
Il existe uneinfinité de ces motis en: a + b et b – a carrés. |
|
|
|
||
|
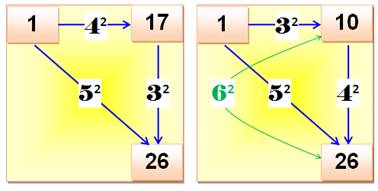
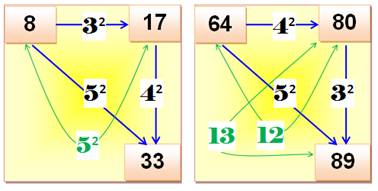
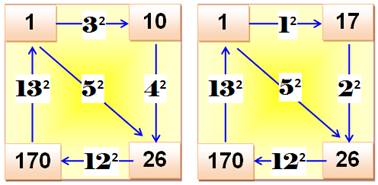
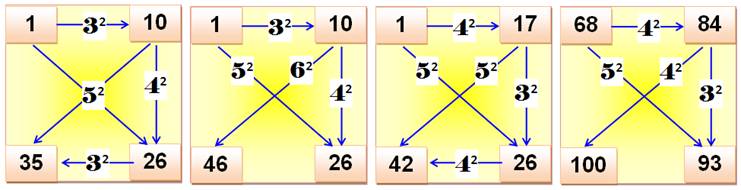
Triplet simple Trouvez trois nombres a, b
et c tels que: b – a = n² c – b = m² c – a = p² Identifiez les cas ou les
sommes sont également des carrés (vert) Le premier exemple ci-contre
donne: 17 – 1 = 4² 26 – 17 = 3² 26 – 1 = 5² Triplets incomplets (une ou deux sommes sont des
carrés) Trois des exemples montrent
une ou deux sommes carrées (vert). Le premier triplet pour lequel
deux sommes sont également des carrés est (en
bas à droite): (64, 80, 89) Le suivant, s'il existe, est
très grand. |
Exemples
Remarquez bien que l'on passe du cas 1 au cas 4 (motif 4², 3², 4²) en ajoutant
63 aux quatre nombres. De même du cas 2 au cas 3 (motif 3², 4², 5²) en
ajoutant 7. Propriété Vous avez reconnus les triplets de Pythagore. Ici le plus célèbre en (3, 4, 5). Les
triplets simples sont en nombre infini. |
|
|
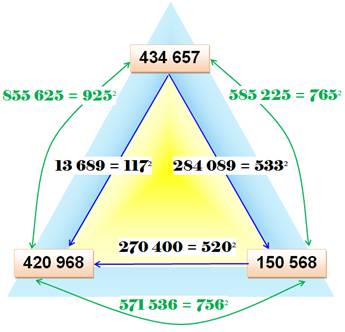
Triplets complets (les trois sommes sont
également des carrés) Le plus petit triplet
complet est composé de nombres à six chiffres. En bleu, différences et vert, les sommes. |
|
|
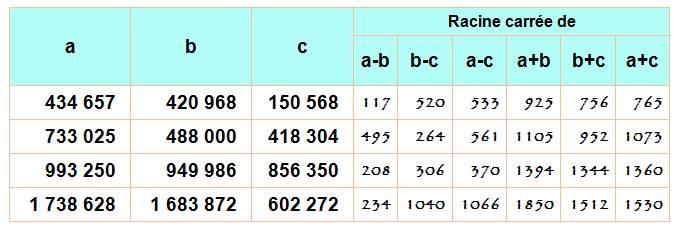
Les quatre plus petits triplets (le deuxième fut
découvert par Euler)
|
|
|
Les
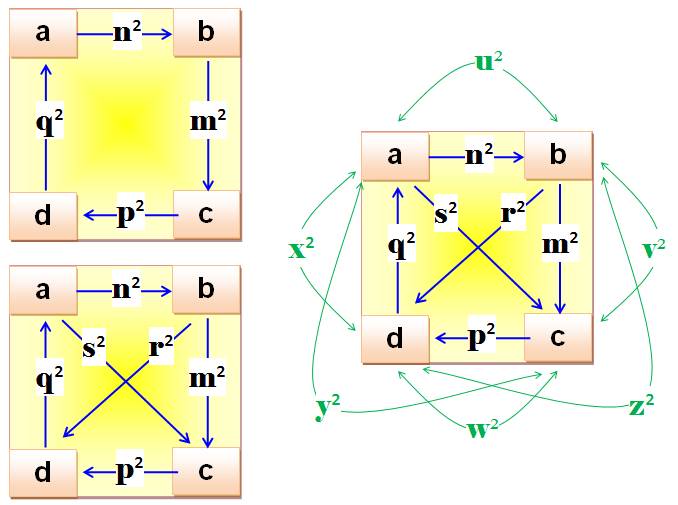
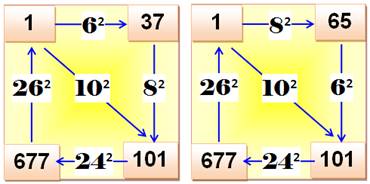
quatre nombres à trouver sont a, b, c et d. Quadruplet
simple: les différences sur le périmètre
sont des carrés. Quadruplet
complet: les différences sur les
diagonales sont des carrés. Super quadruplet: certaines sommes sont des
carrés.
Le
problème d'Ozanam-Rolle consiste à trouver un super quadruplet: Trouver quatre nombres tels que la
différence entre paires est un carré et, en plus, la somme des trois premiers
est également un carré.
|
|
Né
dans une famille aisée. Après des études religieuses forcées par son père, à
sa mort, il se consacre aux mathématiques. 1655
– À 15 ans, il écrit son premier traité. Il
donne des cours de maths à Lyon puis à Paris. 1670
– Publie des tables de logarithmes et de trigonométrie, les plus précises de
l'époque. 1690
– Dictionnaire des mathématiques. 1693
– Cours de mathématiques en cinq volumes. 1694
– Récréations mathématiques et physiques. 1707
– Membre de l'Académie des sciences (créée en 1666 par Colbert). Il
a écrit au moins quatorze livres de maths. Il aimait à
poser des colles à ses contemporains dont Leibniz (1646-1716). |
Voir Contemporains / Énigme des cailloux / Jeu de 100 /
Chèvre,
chou et loup / Les
tonneaux / Les ouvriers dans
les champs / Le nombre
treize
|
|
||
|
Quadruplet simple Trouvez trois nombres a, b,
c et d tels que: b – a = n² c – b = m² d – c = p² d – a = q² Les carrés se trouvent sur
le périmètre. Il y en a une infinité. Quadruplet complet Le quadruplet est complet si
les deux différences sur les diagonales
sont aussi des carrés b – d = r² c – a = s² Ils sont très rares! Imposer
une somme carrée est un véritable défi. Michel Rolle à trouver un tel
quadruplet dont les quatre nombres ont sept chiffres. Il a mis le problème en équation avec des
polynômes de degré élevé. Puis il a encadré les racines en utilisant la
méthode cascade de son invention. Aujourd'hui la résolution formelle fait appel aux
fonctions elliptiques |
Exemples de quadruplets simples
Ces quatre exemples sont construit sur le même motif de départ (1, 2²,
2). Ajouter la même constante à chacun des quatre nombres conserve le
quadruplet. |
|
Voir Brève
669
|
Quadruplet incomplet: périmètre + une diagonale
Quadruplet incomplet: deux diagonales + deux ou
trois côtés
|
|
Malgré
mes recherches, je ne connais pas le quadruplet trouvé par Rolle, ni même
aucun super quadruplets. Notez
bien que le quadruplet est constitué en fait de quatre triplets de Pythagore
emboités. De plus la somme des carrés du périmètre est égale à la somme des
carrés des diagonales. Est-ce une piste de recherche? |
![]()
|
Suite |
|
|
Débutants |
|
|
Voir |
|
|
Livre sur Internet |
|
|
Cette page |
![]()