jeu de taquin

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 17/09/2023 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Jeu de plateau
Débutants Général	Pousse-pousse			Glossaire Général
INDEX Jeux	Taquin	Âne rouge	Cavalier
		Sommaire de cette page >>> Sam Lyod >>> Résolution >>> Taquin – Résolution détaillée >>> Faisabilité >>> Coefficient de désordre >>> Propriétés – Théorie >>> Généralisation

JEU de TAQUIN

PUZZLE 14-15

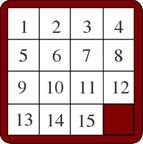
PUZZLE de Sam Loyd

Jeu sur un damier de 4 x 4 cases comportant 15 pions numérotés de 1 à 15. Ces pions ne peuvent se déplacer sur le plateau que par glissement dans la seule case vide à un moment donné. Le jeu consiste à remettre les pions dans l'ordre numérique, comme sur cette figure.

En inversant deux pièces (ce qui exige de le démonter), le taquin devient infaisable. Voir ci-dessous, un peu de théorie.

Anglais: Puzzle of Taquin, Game of Taquin, Game of 15, Sam Loyd's Fifteen

Samuel LOYD (1841-1911)

Célèbre créateur de jeux mathématiques.

Problèmes d'échecs.

Il a popularisé le taquin dont il revendique l'invention (1891)

Il publie un ouvrage détaillé sur le Tangram en 1903

Livres:

Cyclopedia of Puzzles (1914).

Le huitième livre de Tan: 700 dessins de Tangram.

Note: Loyd est la bonne orthographe (et non Lloyd)

Voir Contemporains / Défi de l'étoile / Énigme des trois maisons

Résolution

Étape 1

Faire les 2 premières rangées du haut.

Étape 2

Pour les 2 rangées du bas, procédez par colonne de gauche à droite comme indiqué ci-dessous.

Colonne

Pour cela, amenez les deux pions dans l'ordre pour chaque colonne.

TAQUIN – Résolution détaillée

Première étape simple

Faire les deux premières rangées

1	2	3	4
5	6	7	8
10	9	11	12
	14	15	13

Deuxième étape

Faire les restes de colonne en partant d'un bout (gauche)

pour finir de l'autre (droite)

Attention, il faut préparer deux pions à la fois

Dans l'exemple, il faut préparer 9 et 13

1	2	3	4
5	6	7	8
10	9	11	12
	13	15	14

La disposition semble favorable:

on a bien 9 et 13 l'un en dessous de l'autre

Pourtant, ça ne marche pas!

Faisons glisser les pions

10	9	11
	13	15

9	13	11
10		15

13		11
9	10	15

Ils sont à l'envers!

Deuxième étape: colonne 1

Reprenons autrement

10	9	11
	13	15

Le neuf fait 3/4 de tour

10		11
13	9	15

10	11	15
13		9

10	11	15
13		9

10	15	9
13	11

On met le 13 en position d'attente du 9

10		9
13	15	11

13	10	9
	15	11

On accroche le 9 au 13

13		9
15	10	11

13	9
15	10	11

Une dernière noria

13	9	11
	15	10

9		11
13	15	10

En voici deux en bonne position!

Redonnons le taquin complet

1	2	3	4
5	6	7	8
9		11	12
13	15	10	14

Deuxième étape: colonne 2

	11	12
15	10	14

Les deux pions à placer sont 10 et 14

Ils sont dans le bon ordre

15	11	12
10	14

	15	11
10	14	12

10	15	11
14		12

Redonnons le taquin complet

1	2	3	4
5	6	7	8
9	10	15	11
13	14		12

Deuxième étape: colonnes 3 & 4

Les pièces suivantes se placent automatiquement*

1	2	3	4
5	6	7	8
9	10	15	11
13	14		12

1	2	3	4
5	6	7	8
9	10	11
13	14	15	12

1	2	3	4
5	6	7	8
9	10	11	12
13	14	15

FIN

FAISABILITÉ

Historique

Le premier jeu de taquin connu date de 1880 et il est de Noyes Chapman.

Sam Loyd (1841 - 1911), le plus grand faiseur d'énigmes, a popularisé le jeu de Taquin, un équivalent pour l'époque du cube de Rubic d'aujourd'hui.

Le jeu qu'il proposait était le 14-15. Il s'agissait de remettre les pions mobiles dans l'ordre séquentiel correct.

Loyd promettait un prix à celui qui y arriverait. Il était, en fait, infaisable …

Le taquin a mis plusieurs mois avant de connaître la notoriété au fil des publications d'articles dans la presse, comme ce fut le cas du Rubik's Cube. Désormais, avec Internet, la diffusion est instantanée, comme cela s'est passé pour le célèbre et additif jeu 2048.

On a prouvé par ordinateur que le jeu de taquin n'exige jamais plus de 80 mouvements.

Généralisation

L'étude de la faisabilité du jeu de Taquin est basée sur la mise en évidence d'un invariant.

De nombreuses démonstrations procèdent ainsi, en utilisant des invariants :

le Théorème de Fermat-Wiles

la théorie des nœuds

etc.

Voir, ci-dessous, le principe de caractérisation de la faisabilité basé sur le calcul d'un coefficient de désordre, et la détermination d'un invariant.

Coefficient de désordre
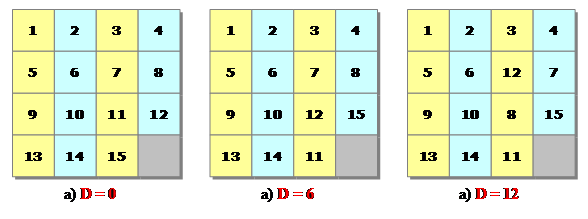
On définit un coefficient de désordre (D) qui donne la quantité de touches dans le désordre.
Bon ordre D = 0	12 avant 11 15 avant 13 15 avant 14 15 avant 11 13 avant 11 14 avant 11 D = 6	Même démarche D = 12

Propriétés - Théorie

D est toujours pair :

tant que le carré libre est en bas à droite, n'importe quel déplacement des touches donnera D = 2n.

Le fait que D soir PAIR est

une qualité intrinsèque des arrangements en partant de l'ordre correct du départ.

C'est un INVARIANT.

L'arrangement de Loyd, dans lequel

le 14 et le 15 sont inversés au montage du jeu

présente un désordre de 1, impair.

Cet arrangement n'est donc pas un arrangement dérivé de l'arrangement initial correct.

Il n'est pas possible de revenir par simple glissement des touches à l'ordre correct.

Généralisation

De nombreuses démonstrations procèdent ainsi: on cherche un invariant.

Un invariant offre une stratégie importante dont l'effet est de démontrer qu'on ne peut pas passer d'un objet à un autre. Une telle démarche est employée pour démontrer le Théorème de Fermat-Wiles.

On l'utilise aussi dans la théorie des nœuds:

Est-il possible de transformer un nœud en un autre par torsion et bouclages, sans les couper ?

On essaie de trouver une propriété des nœuds qui ne peut pas être annulée par les transformations envisagées.

On calcule cette propriété pour le nœud de départ et celui d'arrivée.

Si les valeurs sont différentes, la conclusion est qu'il est impossible de passer de l'un à l'autre.