|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
PUISSANCE de 2 Approche Connaissance des
puissances de deux. |
|
|
||
|
|
1, 2, 4, 8, 16, 32, 64, 128 … 1024 2 6 = 64 210 = 1024 220 vaut un peu plus d'un million 1024 octets = 1 koctets
(français) 1024 bytes = 1 kbytes (anglais) |
|
|
|
||
|
|
Exemple de
lecture du tableau 256 = 2 8 = 44
= 162 1024 = 210 = 45
= 322 |
|
|
|
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
|
2 |
1 |
|
||||||||
|
4 |
2 |
1 |
|
|||||||
|
8 |
3 |
1 |
|
|||||||
|
16 |
4 |
2 |
1 |
|
||||||
|
32 |
5 |
|
|
|
1 |
|
|
|
|
|
|
64 |
6 |
3 |
2 |
1 |
|
|||||
|
128 |
7 |
1 |
|
|||||||
|
256 |
8 |
4 |
2 |
1 |
|
|||||
|
512 |
9 |
3 |
1 |
|
||||||
|
1 024 |
10 |
5 |
|
|
2 |
|
|
|
|
1 |
|
2 048 |
11 |
|
||||||||
|
4 096 |
12 |
6 |
4 |
3 |
2 |
|
||||
|
8 192 |
13 |
|
||||||||
|
16 384 |
14 |
7 |
2 |
|
||||||
|
32 768 |
15 |
|
5 |
|
3 |
|
|
|
|
|
|
65 536 |
16 |
8 |
4 |
2 |
|
|||||
|
131 072 |
17 |
|
||||||||
|
262 144 |
18 |
9 |
6 |
3 |
2 |
|
||||
|
524 288 |
19 |
|
||||||||
|
1 048 576 |
20 |
10 |
|
5 |
4 |
|
|
|
|
2 |
|
2 097 152 |
21 |
7 |
3 |
|
||||||
|
4 194 304 |
22 |
11 |
|
|||||||
|
8 388 608 |
23 |
|
||||||||
|
16 777 216 |
24 |
12 |
8 |
6 |
4 |
3 |
|
|||
|
33 554 432 |
25 |
|
|
|
5 |
|
|
|
|
|
|
67 108 864 |
26 |
13 |
|
|
|
|
|
|
|
|
Voir Multi-puissances / Courbe du nénuphar /
Table
des puissances de 2 avec mise en valeur des derniers chiffres
|
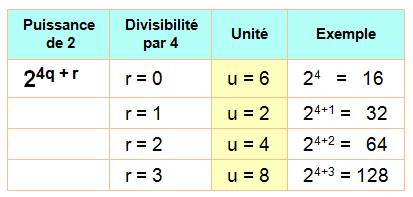
Les
unités des puissances de 2 se répètent
selon un cycle de quatre valeur: 2, 4, 8, 6. Soit le tableau résumé suivant:
|
Le final des puissances
de 2 est égal à n chiffres de l'exposant
|
Exemple: 236 = 68719476736 Liste: 14, 36, 736, 8736, 48736, 948736,
2948736, 32948736, 432948736, 3432948736, 53432948736, 353432948736,
5353432948736, 75353432948736, … OEIS A121219 Chacun,
à partir de 36, est égal au précédent avec un chiffre de plus à gauche. |
|
|
||
|
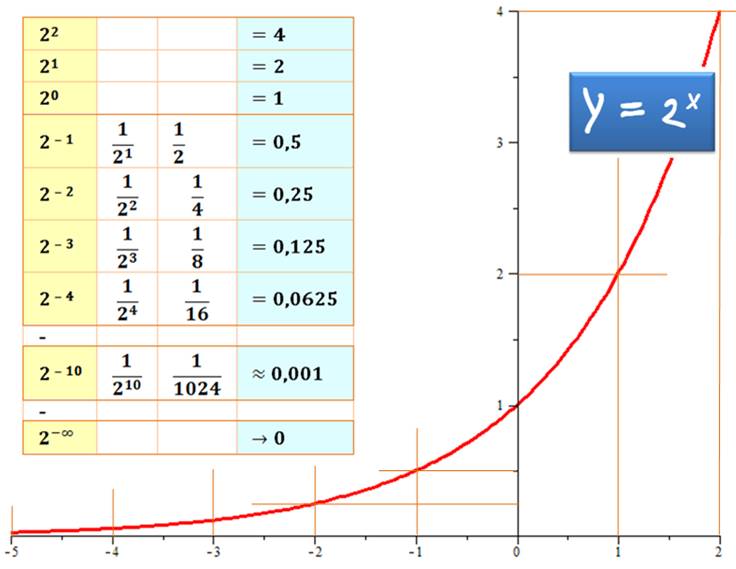
et
on visualise leurs valeurs.
Exemple 42
= 24 43
= 26 En effet 4n
= (2 x 2)n = 2n . 2n = 22n
Exemple 162
= (24)2 = 28 En effet 16n
= (2 x 2 x 2 x 2)n = 2n . 2n . 2n.
2n = 24n
|
|
|
|
|
|
|
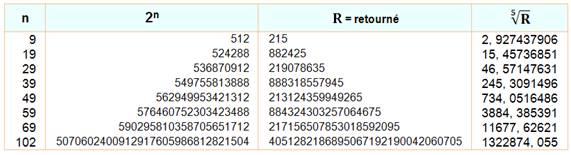
(n2) retourné = m5
?
Exemples: les puissances de 2 successives commençant par 5:
Aucun retourné d'une puissance de 2
Cité par Jean-Paul Delahaye – Pour la
Science janvier 2009
|
|
|
|
|
|
|
|
|
|
||
|
Exemple En passant de la grille du haut à celle du bas, nous avons appuyé sur
la flèche "haut":
|
Accès à ce jeu en ligne >>> |
|
|
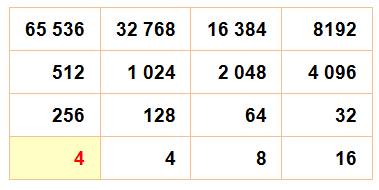
Maximum théorique Le maximum n'est pas 2048 =
211, bien que ce nombre soit déjà difficile à atteindre. En
théorie, c'est 217 = 131
072. Il faut avoir la double
chance d'atteindre cette configuration et d'obtenir un 4 et non un 2 dans la
dernière case (jaune). |
Configuration pour atteindre la maximum théorique
|
|
Voir la vidéo de Micmaths (Michaël
Launay)
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()