|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
PUZZLES
ARITHMÉTIQUES Cryptarithmes – Cryptogrammes Exemple de
recherche de solution. Nous allons
décortiquer toutes les étapes de déduction pour arriver à la solution. Ce puzzle est un classique
anglais, comme le "one two". |
|
|
|
|
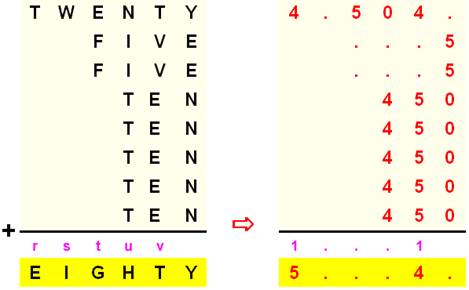
On nous indique
que, pour faire réaliste, TEN est un nombre
divisible par 5.
Voir Anglais |
|
Résolution
pas à pas
|
et
de gauche |
|
|
|
|
N
= 0 ou 5 |
|
|
|
Y
+ 2E + 5N = 10k + Y 2E + 5N = 10k |
|
|
|
N = 0 convient; N
= 5 ne convient pas. |
|
|
|
2E
= 10k E = 5 |
|
|
|
v
= 1 |
|
|
|
r
= 1 T = 4 |
|
|
|
||
|
|
||
|
|
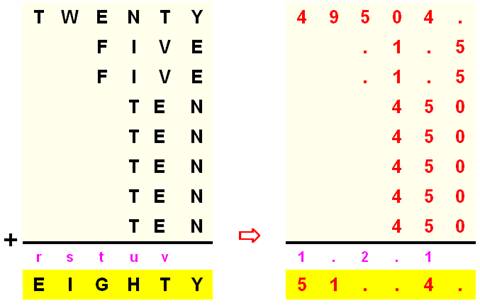
Min: 5 x 4 + 1 + 1 = 22 => t = 2 Max:
5 x 4 + 9 + 9 = 38 => t = 3 |
|
|
|
Min: 5 + 1 + 1 + 2
= 9 => s = 0 Max: 5 + 9 + 9 + 3 = 26 => s = 2 => s = 1 ou 2 |
|
|
|
W
+ 1 = 10 + I => W = I + 9 Impossible ou W
+ 2 = 10 + I => W = I + 8 et
W = 9 et I = 1. |
|
|
|
u
= 2 et H = 2 |
|
|
|
||
|
|
||
|
|
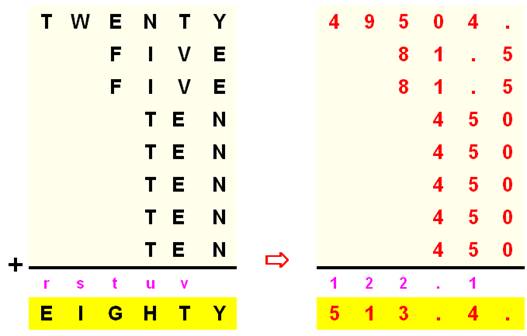
9
+ s = 11 => s = 2 |
|
|
|
5
+ 2F + 2 = 20 + G 2F = G + 13 G
= 1 NON G = 3 et F = 8 G
= 5 NON G=
7 et F = 10 NON |
|
|
|
||
|
|
||
|
|
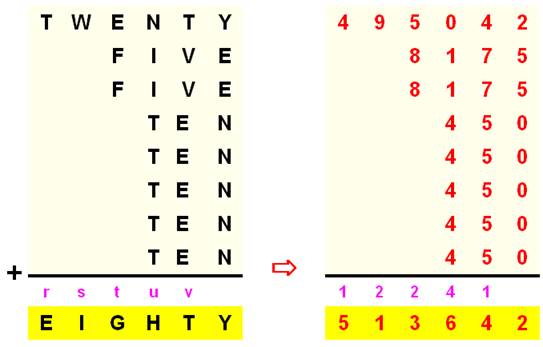
4 + 2V + 5x5 + 1 = 10u
+ 4 2V = 10u – 26 V =
5u – 13 V = 2 ou
7 Somme
4 + 2x2 + 5x5 + 1 = 34 ou 4 + 2x7 + 5x5 + 1 = 44 Soit
u = 3 ou 4 |
|
|
|
2x1
+ 5x4 + 3 = 25 Non car le 5 est déjà affecté. ou 2x1
+ 5x4 + 4 = 26 => H = 6 et V = 7 |
|
|
|
Y = 2 |
|
|
|
||
![]()
![]()