|
||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Lorsque
l'eau de mer gèle, le sel est pour ainsi dire mis de côté. C'est pourquoi
l'Antarctique au complet est le plus grand réservoir d'eau douce du monde. L'inlandsis
qui recouvre la quasi-totalité de la superficie du continent, atteint plus de
4 500 mètres d'épaisseur par endroits ; elle constitue 90 % de l'eau douce du
globe. Source: Géographie de l'Antarctique - Wikipédia |
Voir Remarques in fine / Roman Abysses
|
|
|
|
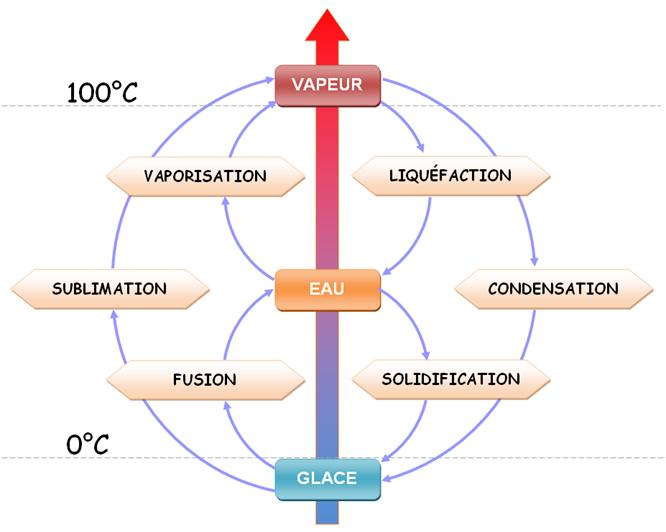
Vocabulaire
du changement d'état
Notes
Énergie
|
|
|
|
|
|
|
|
|
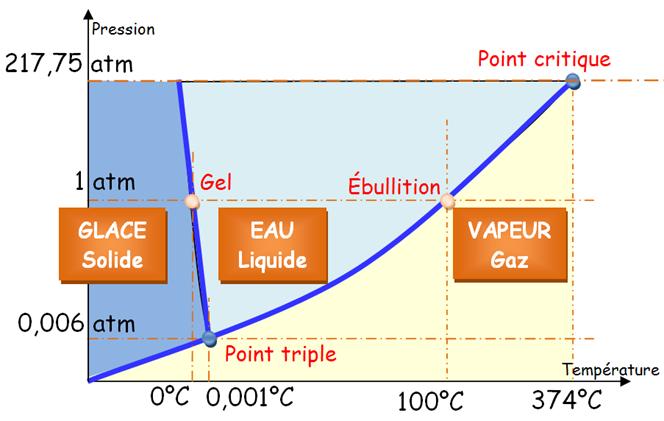
Diagramme
de phase de l'eau (simplifié) ou diagramme de changement d'état |
|
|
Cette pente indique que le corps est plus dense en état liquide qu'en état solide. Ce qui
explique que la glace flotte sur l'eau liquide. L'eau froide est plus lourde que l'eau chaude. Elle est d'autant plus
lourde qu'elle refroidit. L'eau froide salée est la plus lourde de toutes les
eaux. Les courant chauds circulent en surface des océans;
les courants froids en profondeur.
Ce phénomène explique le fonctionnement du patin à glace: sous la
pression du patin, la glace fond et la lame glisse sur un film d'eau liquide.
Aussitôt le patin passé, la pression est relâchée et le film redevient glace. Même phénomène pour un fil de fer sur un pain de glace. Celui-ci est
tendu par des poids qui pendent. En quelques heures, il aura traversé toute
la hauteur du pain en faisant disparaître la trace de son passage au fur et à
mesure de sa progression. Voir Remarques in fine
|
|
|
|
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
Dans le préambule: "Lorsque
l'eau de mer gèle, le sel est pour ainsi dire mis de côté. C'est pourquoi
l'Antarctique au complet est le plus grand réservoir d'eau douce du monde." Ceci est faux, car
l’Antarctique étant une terre émergée, la glace qui le couvre provient des
précipitations et de la condensation, il ne s’agit en aucun cas d’eau de mer
gelée (contrairement à l’Arctique). Lorsque l’eau de mer
gèle, il se forme des poches de saumure incluses dans la glace et dont la
concentration en sel augmente avec le gel. Celles-ci étant prisonnières de la
glace, lorsque vous faites fondre la glace de mer, elle produit de l’eau
salée. Il faut d’abord
éliminer les poches de saumure avant de faire fondre la glace pour récupérer
l’eau douce. |
|
"Ce phénomène
explique le fonctionnement du patin à glace: sous la pression du patin, la glace
fond et la lame glisse sur un film d'eau liquide. Aussitôt le patin passé, la
pression est relâchée et le film redevient glace." Je ne suis pas
d’accord avec cette assertion. Si la lame glisse
effectivement sur un film d’eau qui gèle aussitôt après le passage du patin,
ce n’est pas dû à la pression ! En effet, la glace d’une patinoire est à
une température de -5 à -8°C, il faut une pression 60 à 90MPa pour abaisser
le point de fusion à cette température (coef. dT/dP ~ 10-7 K/Pa (Source wikipedia). La pression exercée
sur un patin étant au plus de l’ordre de 2MPa (100kg x 10 m/s² / 5cm²), la
diminution du point de fusion n’est que de l’ordre du dixième de degré
(0.17°C). Vous pourriez
rétorquer que dans une patinoire, la température de surface de la glace est
proche de zéro degrés, ce n’est certainement pas le cas d’un lac gelé par
-10°C de température extérieure où il est possible de patiner sans peser 6000kg.
Même si le phénomène
physique que vous citez est réel, il n’intervient qu’au second ordre dans le
cas du patinage. La friction est le phénomène responsable de la formation du
film d’eau sous le patin : le coefficient de friction acier/glace étant
de 0.02, un patineur de 100kg se déplaçant à 1m/s dégage 20W de puissance par
friction. C’est la dissipation de cette puissance qui est responsable de la
fusion de l’eau sur un film de l’ordre de 50 microns : M = 100kg, la masse
du patineur S = 5 cm², la surface
de glisse d’un patin de L=40 cm sur l=1.25 mm (p.ex. patin de vitesse) V = 1m/s, la vitesse
de patinage Mu = 0.02 le
coefficient de friction acier/glace Considérant rho =
1g/cm³ (ou 1kg/dm³), la masse volumique de la glace Lf = 333 J/g ou kJ/kg, la chaleur
latente de fusion de l’eau g = 10 m/s²
l’accélération de la pesanteur La puissance
développée P = M g v Mu = 100 x 10 x 1 x 0.02 = 20 W Le travail fourni W =
P t = P L/v = 20 x 0.4 / 1 = 8 J où t est le temps de contact
entre le patin et la glace, longueur du patin divisé par sa vitesse. Avec cette énergie,
on peut faire fondre un volume de glace de m rho Lf
ð m = W / (Rho . Lf)
= 8/333 cm³ soit une épaisseur de m/S = 8/(5x333) =
0.0048 cm, soit 48 microns. Si la glace n’est pas
à 0°C il faut décompter l’échauffement du volume de glace, soit 4.18 J/(dm³ °C) ou 4.18 10-3 J/(cm³ °C). Nous avons
un volume de l’ordre de 0,02 cm³ -> environs 8 10-5 J/°C,
négligeable. D’ailleurs, si vous
aviez raison, un patineur immobile sur une patinoire s’enfoncerait lentement
dans la glace comme le fil sur le pain de glace ! |
Merci à Pol M.
![]()
|
Suite |
|
|
Voir |
|
|
Livres |
|
|
Cette page |
![]()