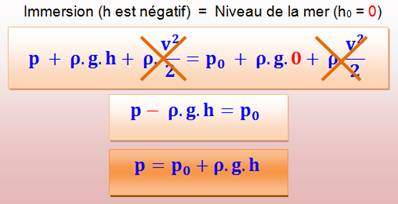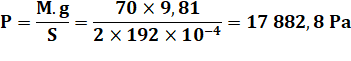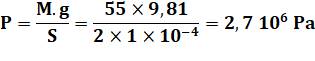|
|||||||||||||||||||||||||||||
![]()
Humour
|
Pascal, Newton et Einstein jouent
à cache-cache. C'est Einstein qui s'y colle. Pascal file et se cache derrière la maison. Newton
reste sur place et dessine un carré autour de lui. Einstein
a fini de compter et découvre Newton devant lui. – Dis donc, Newton, fastoche
pour te trouver ! – Mais, Einstein, tu te trompes de personne, c'est Pascal
que tu viens de trouver. Il montre le carré et poursuit: c'est un newton dans un mètre carré. |
Voir Pensées & humour
|
PRESSION Témoin du poids d'un fluide:
air ou eau ou d'un solide … L'unité de pression dans le système SI est le pascal (Pa) La forme du récipient n'a aucune influence sur la pression. Tous les points situés à la même profondeur sont à la
même pression. Expérience du crève-tonneau réalisée par Pascal: un tonneau et
un fin tube le surmontant. L'eau dans le tube (un litre, par exemple, sur une
hauteur suffisante) fait éclater le tonneau. |
|
|
||
|
Pascal (Pa) Pression exercée par une
force de 1 newton qui se trouve appliquée à une surface de 1 m² En gros: " un dixième de kg sur
1m² " 1Pa = 1
N / m² =
1/100 hPa (hectopascal) = 10
-5 bar =
1/100 mbar (millibar) 1000 hPa = 1 bar 1 hPa = 1 millibar |
Pression
p =
p = Pression hydrostatique
|
|
Voir Les notions de base
|
En gros et pour les retenir |
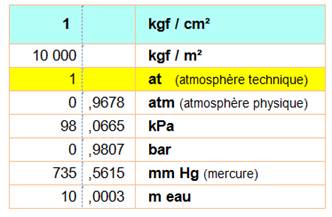
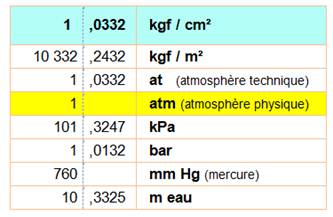
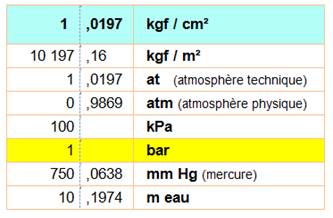
Correspondance avec d'autres unités de pression |
|||||||||||||||||||||||||||
|
Une pression de 1 kilogramme-poids sur un
cm² vaut: 1 kp /
cm² 1 atmosphère 1 bar 100 000 pascals 100 000 N / m² |
Valeur en pascals
|
Voir Unités et
conversion / Voir site Convertworld.com
|
|
||
|
1 bar ou 1000 hPa tous les 10 mètres |
La pression augmente considérablement sous
l'eau. Imaginer la pression sur un sous-marin à 300 mètres d'immersion! 30
bars = 30 kilogramme-poids par cm². |
|
|
|
||
|
|
|||
|
Pour tout fluide en écoulement, la somme de ces trois termes est
constante; que l'on mesure ici ou là, cette expression donne le même
résultat. |
|
||
|
Sans écoulement, le troisième terme disparait, et au niveau de la mer
la hauteur est égale à zéro. |
|
||
|
h est
l'immersion (en mètres); p est la
pression à l'immersion h (en N.m-2); p0
est la pression au niveau de l'eau (pression atmosphérique);
g est l'accélération de la pesanteur: 9,81 m.s-2. 1 bar =
105 pascals. |
p = p0 + 1025 x 9,81 . h p = p0 + 10 055 h p p |
||
|
Nous retrouvons notre résultat: La pression augmente de 1
bar tous les 10 mètres d'immersion. |
|||
Voir Daniel Bernoulli
/ Vitesse du jet
|
|
||
|
Poids
d'une colonne d'air de 1 m² sur toute la
hauteur de l'atmosphère: 101 325 pascals =
1013,25 hPa =
1013,25 millibar » 1 bar =
1 atmosphère » 10 000 kg sur une surface horizontale de 1 m² |
Pression atmosphérique
standard (AOCI) au niveau de la mer à 15°C. Correspondant à 760 mm de mercure. 1 mm Hg |
|
|
Comme
un plongeur subit la pression de l'eau, nous subissons tous la |
|
Historique Galilée À l'époque de Galilée, les fontainiers avaient remarqué que l'eau ne
pouvait être élevée à plus de 10 mètres par une pompe aspirante. Sollicité Galilée
n'avait pas pu expliquer le phénomène. |
|
|
Torricelli C'est Evangelista Torricelli qui, en 1643, comprit le rôle clef de la
force due à la gravitation dans ce problème. Il réalisa une
expérience avec du mercure à la place de l'eau. |
|
|
L'idée de
Torricelli était que l'atmosphère exerce une même force sur tous les objets. |
|
|
Pascal Pascal prolonge le raisonnement: la force
exercée par l'atmosphère est due au poids de l'atmosphère elle-même. Il en déduit que la
pression atmosphérique doit diminuer avec l'altitude. Naturellement, elle
varie aussi selon les conditions météorologiques. |
au Puy de dôme, et à la
Tour Saint Jacques à Paris. |
|
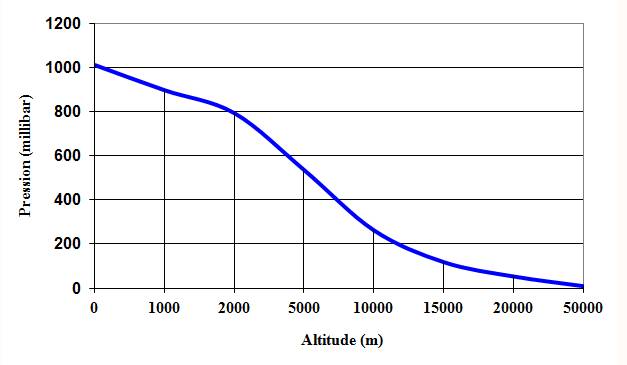
Variation de la pression (standard) en
fonction de l'altitude
Attention:
abscisses
non linéaires
1 mbar tous les 10
mètres jusqu'à 2 000. 1 hPa tous les 15 mètres jusqu'à 10 000.
7 ° C tous les 1 km.
|
|
Voir Pompes et pression atmosphérique
|
|
||
|
|
27
cm x 21 cm x 4,5 cm 2
kg |
|
|
|
F
= m . g = 2kg x 9,81kg.m/s² = 19,62 N |
|
|
|
S = 0,27m x 0, 21m =
0,0567 m² |
|
|
|
P = F/S = 19,62 / 0,0567 = 346,0 Pa |
|
|
|
S = 0,21m x 0, 045m =
9,45 10-3 m² |
|
|
|
P = F/S = 19,62 / 9,45 10-3 = 2
076 Pa |
|
|
|
70 kg Chaque pied: 192 cm² (pointure 43) |
|
|
|
|
|
|
|
55 kg 1 cm² |
|
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Sites |
|
|
Cette page |
![]()