|
||||||||||||
![]()
|
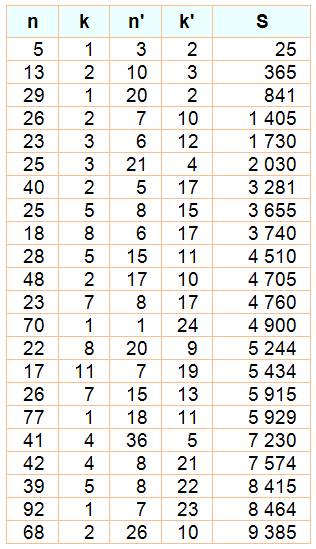
TABLE: Somme des carrés de k nombres consécutifs à partir de n Sn = n² + (n+1)² + … (n+k)² Exemples: S = 10² + 11² + 12² = 365 S =
13² + 14² = 365 |
Voir Somme des carrés de nombres
consécutifs /
Carrés et cubes sommes de trois
cubes consécutifs
|
Triplet
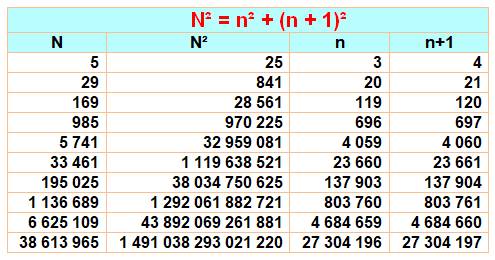
de Pythagore particuliers, comprenant deux nombres voisins. Nombre N dont le carré est la somme du carré de n
et du carré de son suivant (n+1). C'est aussi la suite
de Pell en prenant un nombre sur deux. Chacun est égal à six fois le précédent moins
cinq. |
Voir OEIS A001653 |
|
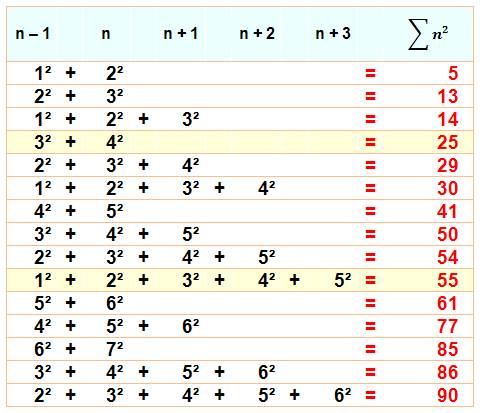
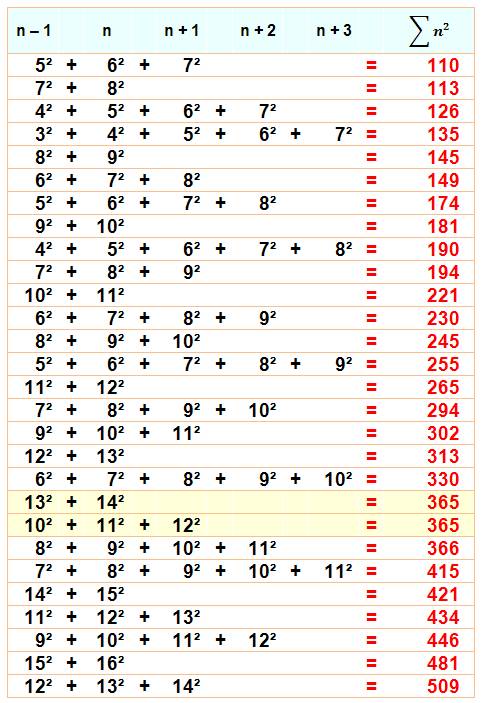
Quelques sommes de deux et de trois carrés consécutifs
|
5 = |
12 + 22 = |
02 + 12 + 22 |
|
365 = |
132 + 142 = |
102 + 112 + 122 |
|
35 645 = |
1332 + 1342 = |
1082 + 1092 + 1102 |
|
3 492 725 = |
1 3212 + 1 3222 = |
1 0782 + 1 0792 + 1 0802 |
|
342 251 285 = |
13 0812 + 13 0822 = |
10 6802 + 10 6812 + 10 6822 |
Voir Sommes deux fois de carrés
consécutifs
|
|
|
|
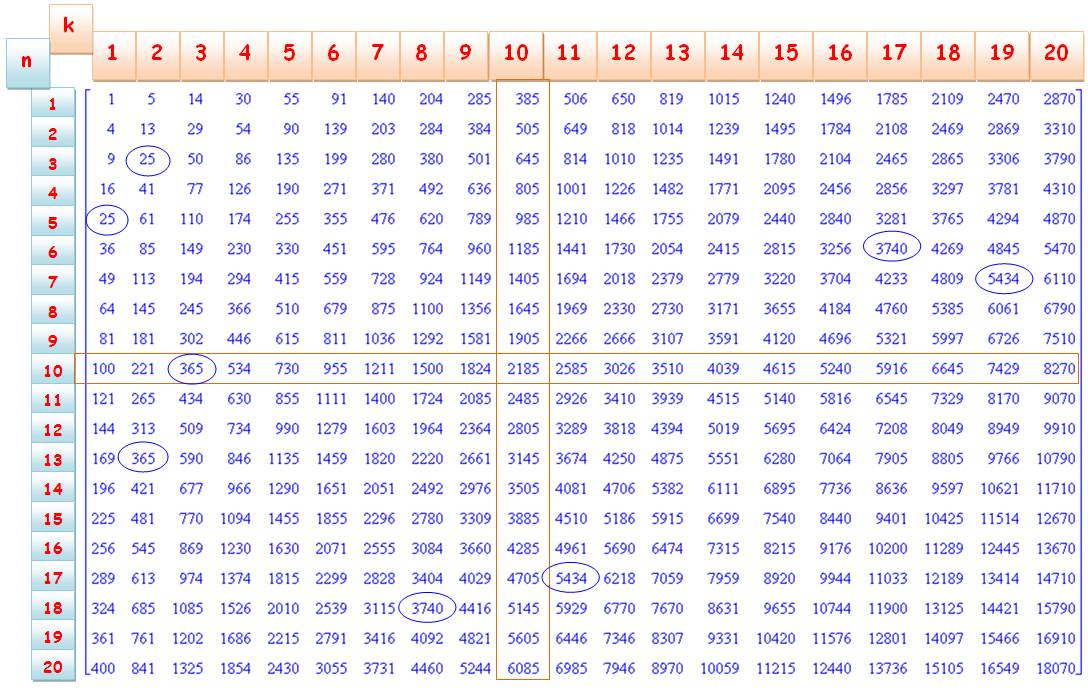
Exemple de lecture: n = 2 et k = 3, on lit 29 car c'est la somme de trois (k = 3) carrés
consécutifs en commençant par 2 (n = 2) :
2² + 3² + 4² = 29. Voir Liste
de ces nombres par ordre croissant >>>
Notes La première colonne donne le carré simple. La première ligne donne les nombres pyramidaux carrés. Les nombres entourés sont les seuls à être
répétés: quatre couples; Dont 365, le
seul avec tous ses nombres consécutifs: 10² + 11² + 12² = 13² = 14² = 365. La colonne de vingt termes de suite se
termine par un 0.. La colonne de dix termes de suite se termine
par un 5. Normal! Sur dix termes la somme des unités des carrés est
toujours: 1, 4, 9, 6, 5, 6, 9, 4, 1, 0 dont la somme vaut 45; et voilà notre
5 pour dix termes. Et une somme de 90
pour vingt termes; et voilà notre 0 systématique en dernière colonne à
droite. |
|
Table des somme de carrés de a à b
|
Liste des nombres somme de
puissances consécutives jusqu'à S = 1000 5, 13, 14, 25, 29, 30, 41, 50, 54, 55, 61, 77,
85, 86, 90, 91, 110, 113, 126, 135, 139, 140, 145, 149, 174, 181, 190, 194, 199,
203, 204, 221, 230, 245, 255, 265, 271, 280, 284, 285, 294, 302, 313, 330,
355, 365, 366, 371, 380, 384, 385, 415, 421, 434, 446, 451, 476, 481, 492,
501, 505, 506, 509, 510, 534, 545, 559, 590, 595, 613, 615, 620, 630, 636,
645, 649, 650, 677, 679, 685, 728, 730, 734, 761, 764, 770, 789, 805, 811,
814, 818, 819, 841, 846, 855, 869, 875, 924, 925, 955, 960, 966, 974, 985,
990, 1001, … Même liste avec indication des
bornes [1,2,5], [2,3,13], [1,3,14], [3,4,25], [2,4,29], [1,4,30],
[4,5,41], [3,5,50], [2,5,54], [1,5,55], [5,6,61], [4,6,77], [6,7,85],
[3,6,86], [2,6,90], [1,6,91], [5,7,110], [7,8,113], [4,7,126], [3,7,135],
[2,7,139], [1,7,140], [8,9,145], [6,8,149], [5,8,174], [9,10,181], [4,8,190],
[7,9,194], [3,8,199], [2,8,203], [1,8,204], [10,11,221], [6,9,230],
[8,10,245], [5,9,255], [11,12,265], [4,9,271], [3,9,280], [2,9,284],
[1,9,285], [7,10,294], [9,11,302], [12,13,313], [6,10,330], [5,10,355],
[10,12,365], [8,11,366], [4,10,371], [3,10,380], [2,10,384], [1,10,385],
[7,11,415], [14,15,421], [11,13,434], [9,12,446], [6,11,451], [5,11,476],
[15,16,481], [4,11,492], [3,11,501], [2,11,505], [1,11,506], [12,14,509],
[8,12,510], [10,13,534], [16,17,545], [7,12,559], [13,15,590], [6,12,595],
[17,18,613], [9,13,615], [5,12,620], [11,14,630], [4,12,636], [3,12,645],
[2,12,649], [1,12,650], [14,16,677], [8,13,679], [18,19,685], [7,13,728],
[10,14,730], [12,15,734], [19,20,761], [6,13,764], [15,17,770], [5,13,789],
[4,13,805], [9,14,811], [3,13,814], [2,13,818], [1,13,819], [20,21,841],
[13,16,846], [11,15,855], [16,18,869], [8,14,875], [7,14,924], [21,22,925],
[10,15,955], [6,14,960], [14,17,966], [17,19,974], [5,14,985], [12,16,990],
[4,14,1001], … |
|
|
||
|
Les premières égalités
se lisent:
Au-delà, les égalités
se multiplient. Comme celle-ci: = 18² + … + 69² = 95² + … + 105² |
|
|
![]()
|
Suite |
|
|
DicoNombre |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()