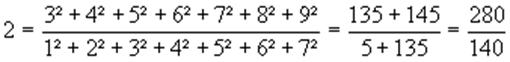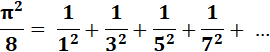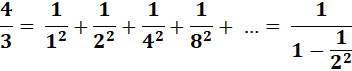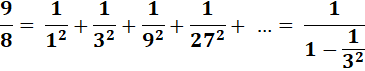|
|||||||||||||||||||||||||||||||||||
![]()
|
FORMES DES CARRÉS Caractérisation Divisibilité par k Quelques
propriétés et curiosités avec les carrés des nombres. Tout carré n² ou n² – 1 est divisible par 3. Tout carré n² ou n² – 1 est divisible par 4. Tout carré n² ou n² – 1 ou n² + 1
est divisible par 5. >>> Le produit ou le quotient de deux
carrés est un carré (entier ou fraction). Tout nombre carré pair est la somme
de quatre carrés identiques; impair, somme d'au plus trois carrés différents.
>>> Tout carré de nombre premier, à
partir de 5, est une multiple de 24 plus 1. >>> |
Magie des nombres
|
111
111 1112 = 123 456 78 9 87
654 321 |
|
Relation entre le
carré d'un nombre et trois
factorielles successives
|
Voir Repunit
/ Pannumérique / Pépites
|
Montrer
qu'il n'existe aucun couple (x, y) tel
que x² + 4y et y² + 4x soient des carrés. |
|
|
||||||||||||
|
Un nombre au
carré est un multiple de 5 ou un voisin. |
||||||||||||
|
Démonstration On développe
le carré de chaque cas de division par 5.
Chaque
expression conduit à un nombre de la forme:
Le
chiffre
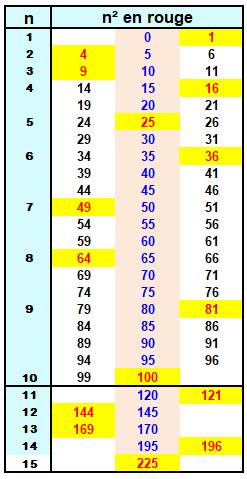
des unités d'un carré sont autour du 0 eu du 5: |
Les nombres carrés sont sur la colonne des
multiples de 5 ou juste voisins
|
|||||||||||
Voir Brève
de maths 476 / Nombre
5
|
|
||
|
Un nombre
premier au carré, sauf 2 et 5, est un multiple de
24 plus 1. |
||
|
Démonstration Un nombre
premier est
de la forme 6k Son carré
Si k est
pair, alors 3k² est pair et 3k² + 1 est impair. Si k est
impair, alors 3k² est impair et 3k² + 1 est pair. Idem avec les igne moins. Dans les deux,
l'un des deux est pair. P² –
1 est divisible par 12 et par 2; donc
par 24. |
|
|
Voir Divisibilité par 24 / Séquence
en 24 / Nombre
24
|
|
|
|
Un nombre au carré ne
change pas de parité. Exemples: 4² =
16; 5² = 25 Explications: Pair: (2k)² = 4k², divisible par 2. Impair: (2k+1)² =
(4k² + 4k) + 1 = 4k(k + 1) + 1, reste un. Tous les carrés sont
de la forme 3k ou 3k + 1. Exemples: 3² =
15 = 3 x 5; 4² = 16= 3 x 5 + 1; 5² = 25 = 3 x 8 + 1 Explications: Avec n = 3h => n² = 9h² = 3 x 3h² Avec n = (3h – 1) => (3h –
1)² = 9h² – 6h + 1 = 3h (3h – 6) + 1 Avec n = (3h + 1) => (3h +
1)² = 9h² + 6h + 1 = 3h (3h + 6) + 1 Tous les carrés sont
de la forme 4k ou 4k + 1. Exemples: 4² = 16 = 4 x 4;
5² = 25 = 4 x 6 + 1; 6² = 36 = 4 x 9;
7² = 49 = 4 x 12 + 1 Explications: Avec n = 4h => n² = 16h² = 4 x 4h² Avec n = (4h – 2)
=> (4h – 2)² = 16h² – 16h + 4 = 4 (4h² – 4h + 1) Avec n = (4h – 1)
=> (4h – 1)² = 16h² – 8h + 1 = 4
(4h² – 2h) + 1 Avec n = (4h + 1)
=> (4h + 1)² = 16h² + 8h + 1 = 4
(4h² + 2h) + 1 |
|
Voir Identités
remarquables / Divisibilité par
3
|
|
|||
|
Tous les carrés sont
des multiples de 5 Exemples
Démonstration |
|||
|
Soit
la division de n
par 5 |
n = 5q + r |
|
|
|
Au carré |
n² = 25q² + 10qr +
r² |
||
|
|
n² = 5 (5q² + 2qr)
+ r² |
|
|
|
Prenons
tous les restes possibles de la division par 5 |
|
||
|
r = 0 |
n² = 5 (5q² + 2qr) |
divisible par 5, reste 0 |
|
|
r = 1 |
n² = 5 (5q² + 2qr)
+ 1 |
reste 1 |
|
|
r = 2 |
n² = 5 (5q² + 2qr)
+ 4 |
reste 4, soit 5 – 1 |
|
|
r = 3 |
n² = 5 (5q² + 2qr)
+ 9 |
reste 9, soit 5 – 1 |
|
|
r = 4 |
n² = 5 (5q² + 2qr)
+ 16 |
reste 16, soit 5 + 1 |
|
|
On
trouve toujours un des cas
suivants: |
5k 5k – 1 5k + 1 |
|
|
|
|
|
|
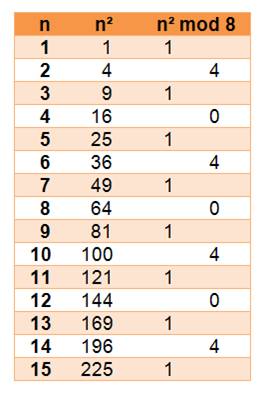
Tous les carrés sont
des multiples de 8 ou des multiples de 8
+ 1 ou des multiples de 8
+ 4 n² = {0, 1, 4} mod 8 Voir Modulo Tous les carrés de
nombres impairs sont des multiples de
8 + 1 Impair² = 1 mod 8 Voir Démonstration et exemples Exemples
|
|
|
|
|
|
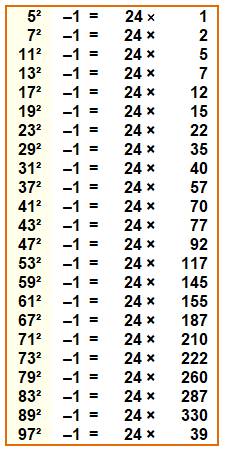
n² = 24 k + 1 pour tout n premier
> 3 et en général, pour tout n impair non multiple de 3. Exemples 5² =
24 + 1 7² =
48 + 1 11²
= 120 + 1
Etc. |
|
Voir Démonstration / Séquence en 24
|
|
|
|
Le carré d'un nombre
premier (> 5) se termine par 1 ou
9. En effet l'unité d'un nombre premier est 1, 3 7 ou 9; et l'unité de leur carré est, 1, 9, 9 ou 1. |
|
![]()
|
|
||
|
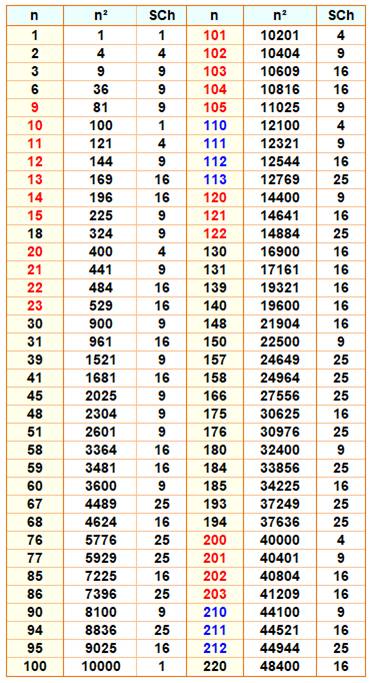
Nombre,
son carré et la somme de ses chiffres lorsque celle-ci est un carré. En rouge
ou bleu, suite de nombres dont la somme des chiffres du carré est un carré. Certaines
valeurs sont triviales comme 10, 20 ou 30. |
|
|
|
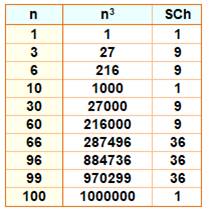
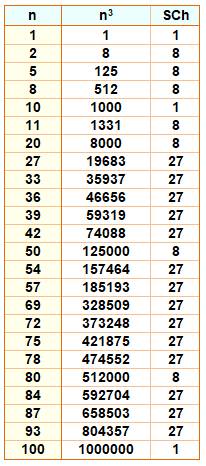
Somme des
chiffres du cube = carré & Somme des
chiffres du cube = cube |
|
|
|
|
|
|
Carrés comportant deux chiffres (n suivi
de son carré) [11, 121], [12, 144], [15, 225], [21, 441], [22, 484], [26, 676],
[38, 1444], [88, 7744], [109, 11881], [173, 29929], [212, 44944], [235, 55225], [264, 69696], [3114, 9696996], [81619, 6661661161],
… En rose, les palindromes; liste pour n jusqu'à dix
millions. Carrés les plus petits comportant k
chiffres: n, n², ses chiffres 1, 1, {1} 4, 16, {1,
6} 13, 169,
{1, 6, 9} Ex: 13² = 169 est le plus petit carré
comportant trois chiffres quelconques 32, 1024,
{0, 1, 2, 4} 113,
12769, {1, 2, 6, 7, 9} 322,
103684, {0, 1, 3, 4, 6, 8} 1017,
1034289, {0, 1, 2, 3, 4, 8, 9} 3206,
10278436, {0, 1, 2, 3, 4, 6, 7, 8} 10124,
102495376, {0, 1, 2, 3, 4, 5, 6, 7, 9} 32043,
1026753849, {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} Plus petit carré pannumérique (10) 99 066² = 9 814 072 356, le plus grand Carrés les plus petits comportant k
chiffres successifs de 1 à 9: n, n², ses chiffres 1, 1, {1} 11, 121,
{1, 2} 111,
12321, {1, 2, 3} Ex: 111² = 12321 est le plus petit carré
comportant les trois premiers chiffres. 182,
33124, {1, 2, 3, 4} 368,
135424, {1, 2, 3, 4, 5} 1112,
1236544, {1, 2, 3, 4, 5, 6} 5116, 26173456,
{1, 2, 3, 4, 5, 6, 7} 5904,
34857216, {1, 2, 3, 4, 5, 6, 7, 8} 11826, 139854276,
{1, 2, 3, 4, 5, 6, 7, 8, 9} Plus petit carré pannumérique
(9) 30 384² = 923
187 456, le plus grand Les
plus petits carrés qui associés couvent tous les chiffres Avec deux
carrés et nombres de 1 à 100 (le premier nombre est le plus petit) 18²
et 867² => 324 et
751689 42²
et 945² => 1764 et 893025 (avec 0) Avec deux
carrés et somme des nombres minimale 57² et 126² => 3249 et 15876 (somme 183) 126² et 153² => 15876 et 23409 (avec 0;
somme 279) Avec trois
carrés et nombres de 1 à 100 (le premier nombre est le plus petit) 4², 28²,
73², => 16, 784, 5329 9², 48²,
87² => 81, 2304, 7569 (avec 0) Avec trois
carrés et somme des nombres minimale 5², 28²,
37² => 25, 784, 1369 (somme 70) 18², 24²,
33² => 324, 576, 1089 (avec 0; somme 75) Avec
quatre carrés et nombres de 1 à 100 (le premier nombre est le plus petit) 1², 5²,
22², 86² => 1, 25, 484, 7396 1², 6²,
28², 95² => 1, 36, 784, 9025 (avec 0) Avec
quatre carrés et somme des nombres minimale 3², 9²,
18², 24² => 9, 81, 324, 576 (somme 54) 3², 9²,
24², 48² => 9, 81, 576, 2304 (avec 0; somme 84) |
|
Suite Carrés
avec chiffres répétés / Brève de
maths 474
Voir Fraction – Glossaire
|
|
|||
|
32 043 2 = |
1
026 753 849 |
||
|
99 066 2 = |
9
814 072 356 |
Pannumérique |
|
|
36 363 636 364 2 = |
13
223 140 496 13 223 140 496 |
Nombre
"jumeaux" |
|
|
505 025 2 = |
255
050 250 625 |
Le
nombre est dans son carré |
|
|
146 509 717 2 = |
21
465 097 175 420 089 |
'' |
|
|
495 475 2 = |
245
495 475 625 |
Le
nombre est dans son carré, au centre |
|
|
625 000 2 = |
390
625 000 000 |
'' |
|
|
971 582 2 = |
943
971 582 724 |
'' |
|
|
177 656 344 2 = |
31
561 776 563 446 336 |
'' |
|
|
18 212 890 625 2 = |
331
709 384 918 212 890 625 |
Même
terminaison (automorphique) |
|
|
|
|||
|
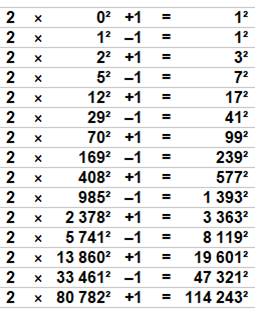
5 = |
12 + 22
= |
02 + 12 + 22 |
|
|
365 = |
132 + 142
= |
102 + 112 + 122 |
|
|
35 645 = |
1332 + 1342
= |
1082 + 1092 + 1102 |
|
|
3 492 725 = |
1 3212 + 1 3222
= |
1
0782 + 1 0792 + 1 0802 |
|
|
342 251 285 = |
13 0812 + 13 0822
= |
10
6802 + 10 6812 + 10 6822 |
|
Voir Suite
/ Nombres consécutifs
Voir Identité
d'Euler / Euler
/ Progressions géométriques
|
|
|
|
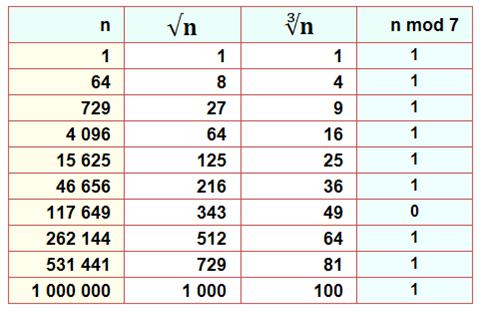
Un nombre carré et
cube à la fois est de la forme 7k ou 7k + 1. Cette table donne toutes les valeurs pour n Ce sont les puissances 6 des nombres de 1 à 10.
Preuve Si un nombre est un carré et un cube, il est aussi une
puissance sixième. Or, avec le petit
théorème de Fermat et si n non divisible par p
Et, si divisible, alors le reste de la division par 7
est nul. |
|
Voir Nombres 64 / 729 / 4 096 / Calcul
d'Inaudi (calculateur prodige)
|
|
|
|
D'après Fermat,
il n'existerait que 5 nombres entiers dont le carré augmenté de 2 donnerait
un cube: Exemples 5² + 2 =
33 25 + 2 = 27 Il se trompait: il n'existe que cette seule
solution à l'équation: Y²
+ 2 = X3 |
|
|
Problème:
Montrer qu'il n'existe aucun couple (x, y) tel que x² + 4y et y² + 4x soient
des carrés; x et y sont des entiers positifs. Exemple:
x = 2 et y = 3. Alors: x² + 4y = 16 =
4² et y² + 4y = 15 = 4² – 1. Raté à une unité près
(coquetterie: avec le même carré:4²). C'est le seul exemple
à 1 près. Suivant, avec un écart
de 3: x=3 et y=4; x²+4y = 25 et y²+4x
= 28. Solution
|
![]()
|
Suite |
|
|
Voir |
|
|
Dicinombre |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/DeuxCarr.htm |
![]()