|
Édition du: 27/10/2024 |
|
INDEX |
Partitions – Goldbach |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
Pair = (Impair + Impair)
Composés Propriété de la
partition des nombres pairs du type Goldbach. |
||
|
Terminale |
Sommaire de cette page >>> Approche de la propriété >>> Démonstration de la propriété >>> Table de partition des nombres pairs en somme
de deux impairs composés jusqu'à 100 |
Débutants Glossaire |
|
Propriété À partir de 40, tous les nombres pairs sont somme de deux nombres impairs
composés. |
Exemples 40 =
15 + 25 42 = 9 +
33 44 = 9 + 35 |
|
|
Nombres pairs jusqu'à 30 Cette liste
des plus petits nombres composés
impairs permet d'établir les possibilités pour les plus petits nombres. Sachant que 1 n'est ni premier ni composé, il est
exclut. Alors le plus petit nombre impair
composé est 9. Avec ce nombre, il est
possible d'atteindre le nombre 9 + 9 = 18, et aucun autre plus petit. Le suivant sera 9 + 15 = 24, puis 15 + 15 = 30. Premier résultat Tous les nombres pairs de 2 à 28 ne sont pas
somme de deux impairs composés. |
Liste des composés impairs 9, 15, 21, 25, 27, 33, 35, 39, 45, 49, 51, 55,
57, 63, 65, 69, 75, 77, 81, 85, 87, 91, 93, 95, 99 |
|
|
Grands nombres Soit X un grand nombre pair. Alors, on analyse les différences X – 9, X – 15,
X – 21, etc. en prenant la suite des nombres impairs composés. Si une seule de ces différences est composée,
alors la propriété est vérifiée. Inversement, il faudrait que toutes ces
différences soient des nombre premiers pour infirmer la propriété. On tente une analyse de type modulo 3:
un nombre est divisible par 3 ou a un reste de 1 ou un reste de 2. |
Nombre pair somme de deux nombres X = A + B X est pair, et A et B sont composés impairs. |
|
|
Nombre pair X = 3k Si X est un multiple de 3, alors A = X – 9 est à
la fois impair et multiple de 3. (cf. X pair – 3 impair = impair & X multiple 3 et 9 multiple de3 => A = X – 9 multiple de 3) Notez que 12
ne marche pas, car 12 = 9 + 3 Mais, cette propriété est
vraie pour tous les nombres pairs multiples de 3 à partir de 18. |
Plus petits cas avec X = 3k X = 18 =
9 + 9 X = 24 = 15 + 9 X = 30 = 21 + 9 X = 36 = 27 + 9 X = 42 = 33 + 9 |
|
|
Nombre pair X = 3k + 1 Le nombre 25 est un multiple de 3 plus 1. Si X est un multiple de 3 plus 1, alors X – 25,
est impair et divisible par 3. Notez que 28
ne marche pas, car 28 = 25 + 3 Mais, cette propriété est
vraie pour tous les nombres pairs multiples de 3 + 1 à partir de 34. |
Plus petits cas avec X = 3k + 1 X = 34 =
9 + 25 X = 40 = 15 + 25 X = 46 = 21 + 25 |
|
|
Nombre pair X = 3k + 2 Le nombre 35 est un multiple de 3 plus 2. même raisonnement que précédemment. Notez que 38
ne marche pas, car 38 = 35 + 3 Mais, cette propriété est
vraie pour tous les nombres pairs multiples de 3 + 1 à partir de 44. |
Plus petits cas avec X = 3k + 2 X = 44 =
9 + 35 X = 50 = 15 + 35 X = 56 = 21 + 35 |
|
|
Limite basse Un nombre X (pair ou non) se retrouve dans l'un
des cas examinés (X = 3k ou X = 3k + 1 ou X = 3k + 2). Donc tous les nombres pairs à partir de 44 sont
la somme de deux nombres impairs composés. De plus, les exemples montent que 42 et 40
partagent cette propriété La propriété est bien vraie à partir de 40. |
Le plus grand nombre pair qui n'est pas somme de deux nombres impairs
composés est le nombre 38. Le plus petit nombre pair qui est somme de deux nombres impairs composés
est 40. Plus le nombre pair est grand, plus la quantité
de sommes d'impairs composés est grande. |
|
Table de
partition des nombres pairs en somme de deux impairs composés jusqu'à 100
M3 indique le reste de la division de N par
3.
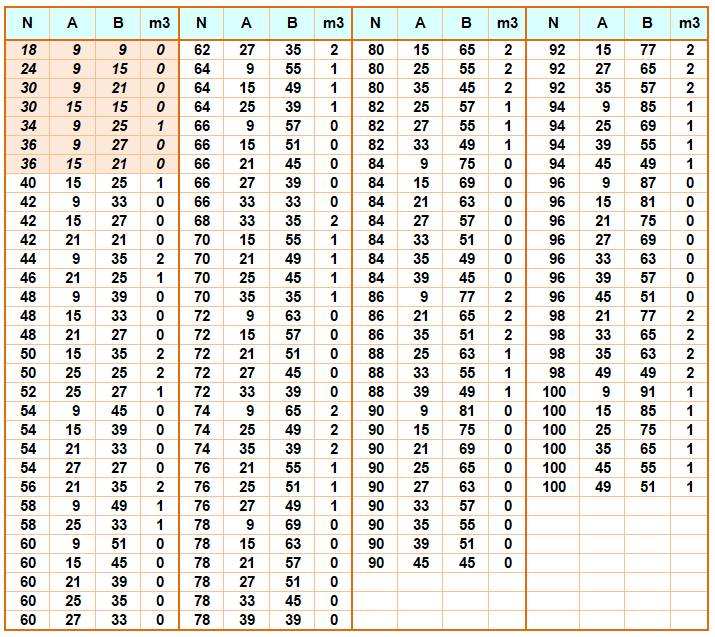
Haut de page (ou
double-clic)
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |

